Главная | Обратная связь | Поможем написать вашу работу!

Примеры абстрактных автоматов, выполняющих полезные действия

Теория абстрактных автоматов

Владимир 2006

Учебное пособие для студентов очной и заочной форм обучения специальностям
в области вычислительной техники, информатики и управления.

ОГЛАВЛЕНИЕ

Часть 1. Теория абстрактных автоматов…………………………………………………..3

1.1. Общие сведения……………………………..………………………………………..3

1.2. Способы задания автоматов…………………………………………………………4

1.3. Примеры абстрактных автоматов, выполняющих полезные действия…………...6

1.4. Поведение изолированного синхронного автомата………………………………..8

1.5. Регулярные выражения и конечные автоматы…………………………………….10

1.6. Алгоритмы и машины Тьюринга….………………………………………………...11

1.7. Элементы теории формальных грамматик и языков………………………………15

1.8. Условия автоматности отображения………………………………………………..20

1.9. Построение графа автомата по входо-выходным последовательностям…………21

1.10. Преобразование автоматов………………………………………………………….22

Задачи и упражнения.……………………………………………………………………..24

Литература…………………………………………………………………………………25

ЧАСТЬ 1. ТЕОРИЯ АБСТРАКТНЫХ АВТОМАТОВ

Общие сведения

Абстрактный автомат (АА) – дискретный преобразователь информации; представляет собой множество, состоящее из шести элементов:

S = {X, Q, Y, δ, λ, q₁}

S – абстрактный автомат;

X – множество входных символов (входной алфавит автомата):

X = { x₁,..., x_m};

Q – множество состояний автомата:

Q = { q₁,..., q_n};

Y – множество выходных символов (выходной алфавит автомата):

Y = { y ₁,..., y_p };

δ – функция переходов автомата из одного состояния в другое:

q_j = δ(q_i, x_k),

где: q_j – следующее (новое) состояние автомата; q_i – текущее состояние автомата;
x_k – текущий входной символ;

λ – функция выходов:

y_l = λ (q_i, x_k);

q₁ – начальное состояние автомата (применяется также обозначение q₀).

Автомат называется конечным, если множества X, Q, Y – конечны.

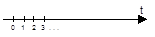
Рис.1. Представление абстрактного автомата

На рис. 1 t – дискретное время: t = nT, где T – интервал (такт), разделяющий дискретные моменты времени; если T = 1, то t = n, т. е. дискретное время сопоставляется упорядоченному ряду натуральных чисел.

Абстрактный автомат (АА) можно рассматривать как "черный ящик" с одним входом и одним выходом, с которым можно экспериментировать, не зная, что находится внутри.

Выходной символ (y_l Î Y) зависит не только от входного символа (x Î X), но и от
того, в каком состоянии (q_i Î Q) находится автомат. Автомат функционирует в дискретном времени; это означает, что элементы описания автомата заданы только в упомянутые выше дискретные моменты.

Представим, что с некоторого начального, например, нулевого момента времени на вход автомата подаются входные символы, образующие входное слово некоторой длины (длина любого i -го слова измеряется числом символов). На выходе получаем выходное слово той же длины (рис. 2).

Рис.2. Преобразование входных слов в выходные

Сказанное означает, что автомат может рассматриваться как преобразователь входных слов в выходные с сохранением длины слов. Символы алфавитов, присутствующие на входе и выходе автомата, будем также называть входными и выходными сигналами.

На практике широкое распространение получили две основные модели, описывающие функционирование АА:

1. Модель Мили;

2. Модель Мура.

Модель Мили.

Законы функционирования автомата Мили представлены следующим образом:

q(t+1) = δ (q (t), x (t))

y (t) = λ(q(t), x(t))

t – текущий момент времени;

t+1 – следующий момент времени;

q(t+1) – состояние автомата в следующий момент времени;

q(t), x(t), y(t) – элементы описания автомата в текущий момент времени.

Модель Мура.

Законы функционирования автомата Мура представлены следующим образом:

q(t+1) = δ (q (t), x (t))

y (t) = λ(q(t))

В модели Мура выходной сигнал явно зависит только от состояния, а косвенно –
и от входного сигнала.

Любой автомат можно спроектировать по той или иной модели.

Способы задания автоматов

Рассмотри два основных способов задания автоматов:

Табличный способ

Автомат Мили

Для автомата Мили табличный способ заключается в построении двух таблиц: таблицы переходов (ТП) и таблицы выходов (ТВ).

x\q	…	q_i	…	x\q	…	q_i	…
. . .				. . .
x_k		d(q_i,x_k)		x_k		l(q_i,x_k)
. . .				. . .

а б

Рис. 3. Табличный способ: а – таблица переходов, б – таблица выходов.

Пример:

а) Таблица переходов

x\q	q₁	q₂	q₃
x₁	q₃	q₁	q₁
x₂	q₂	q₃	q₂

б) Таблица выходов

x\q	q₁	q₂	q₃
x₁	y₁	y₁	y₂
x₂	y₁	y₂	y₁

Автомат Мура

Таблица переходов и таблица выходов объединяются, и добавляется строка
выходных сигналов, соответствующих состояниям автомата. На рисунке 4 показана таблица переходов и выходов для автомата Мура.

	…	l(q_i,x_k)	…
x\q	…	q_i	…
. . .
x_k		d(q_i,x_k)
. . .

Рис. 4. Таблица переходов и выходов

Пример. Таблица переходов и выходов:

	y₁	y₁	y₃	y₂	y₃
x \ q	q ₁	q ₂	q ₃	q ₄	q ₅
x ₁	q₂	q₅	q₅	q₃	q₃
x ₂	q₄	q₂	q₂	q₁	q₁

2. Графовый способ

Автомат представляется ориентированным связным графом (орграфом), вершины которого соответствуют состояниям автомата, а дуги – переходам из состояния
в состояние. Обозначения входных и выходных сигналов распределяются в автоматах Мили и Мура по-разному.

Построим графы для автоматов Мили и Мура по вышеприведенным таблицам:

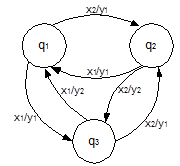
Рис. 5. Представление автомата Мили в виде графа

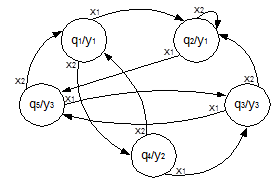
Рис. 6. Представление автомата Мура в виде графа

Замечание: В автомате Мили выходной сигнал вырабатывается при переходе, а
в автомате Мура присутствует в течение всего периода дискретного времени, пока
автомат находится в данном состоянии.

Детерминированный автомат – автомат, в котором имеется полная определенность переходов из всех состояний в зависимости от входных сигналов (под действием одного и того же сигнала автомат не может переходить из любого рассматриваемого состояния в различные состояния). Фрагмент графа, изображенный на рисунке 7, не может относиться к детерминированному автомату.

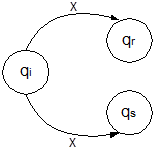
Рис.7. Фрагмент графа, иллюстрирующий неопределенность переходов

Замечание: Недетерминированные (например, вероятностные) автоматы существуют, но их рассмотрение не предусмотрено в данном курсе.

Состояние автомата q_i называется устойчивым, если для любого входного сигнала х_к, такого, что δ(q_s, x_k) = q_i, справедливо соотношение: δ(q _i, x_k) = q_i. (здесь q_s – состояние, предшествующее q_i). Это означает, что, автомат не изменяет своего состояния при повторении на следующем такте сигнала, приведшего его в состояние q_i. Фрагмент графа, иллюстрирующий устойчивость состояния, приведен на рисунке 8.

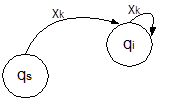
Рис. 8. Устойчивое состояние автомата

Автомат называется асинхронным, если каждое его состояние q_i Î Q (i = 1, …, n) устойчиво; в противном случае автомат называется синхронным. Синхронные автоматы важны для теории, а на практике чаще используются асинхронные; устойчивость состояний в асинхронных автоматах достигается введением специальных сигналов синхронизации.

Примеры абстрактных автоматов, выполняющих полезные действия

1. Автомат для задержки сигнала на один такт (для запоминания на один такт)

Опишем данный автомат таблицами и графом:

Таблица переходов и таблица выходов:

x\q	q₀	q₁	x\q	q₀	q₁
x₀	q₀	q₀	x₀	y₀	y₁
x₁	q₁	q₁	x₁	y₀	y₁

Поскольку автомат является двоичным, введем обозначения: x₀= y₀ = 0; x₁= y₁ = 1.

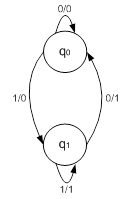
Рис. 9. Граф автомата для задержки сигнала на один такт

Простой анализ показывает, что выходной сигнал в текущем такте повторяет входной, который был на такт раньше.

2. Автомат для проверки двоичной последовательности на четность.

Опишем данный автомат таблицами и графом:

Таблица переходов и таблица выходов:

x\q	q₀	q₁	x\q	q₀	q₁
x₀	q₀	q₁	0	0	1
x₁	q₁	q₀	1	1	0

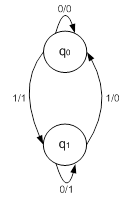
Рис. 10. Граф автомата для проверки двоичной последовательности на четность

Анализ показывает, что «0» на выходе автоматически вырабатывается при четном числе единиц на входе, а «1» на выходе вырабатывается при нечетном числе единиц на входе.

Оба рассмотренных автомата имеют "слабую" память, но слабую в разном смысле.
У первого автомата "короткая" память во времени (помнит только один сигнал).
У второго автомата память "длинная" (длина входной последовательности может быть любой), но он различает (распознает) лишь два класса последовательностей.

3. Автомат для задержки сигнала на два такта.

Автомат имеет четыре состояния, закодированных двумя двоичными разрядами:
q₀= 00; q₁= 01; q₂= 10; q₃= 11.

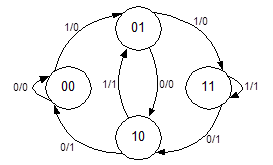
Рис. 11. Граф автомата для задержки сигнала на два такта

Достоинства примененного кодирования:

· первая цифра кода состояния показывает, какой сигнал выдает автомат (он легко преобразуется в автомат Мура); вторая цифра кода показывает, под действием какого сигнала автомат приходит в данное состояние.

· легко проверить, что выходной сигнал повторяет входной через два такта.

4. Двоичный последовательный сумматор, реализованный для одного разряда входного кода.

Автомат имеет два состояния: q₀– нет переноса (сложение цифр операндов не требует учета единицы переноса из предыдущего разряда кода);

q₁– есть перенос (единица переноса должна быть учтена).

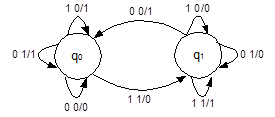
Рис. 12. Граф одноразрядного двоичного последовательного сумматора

В числителе "дроби", записанной при каждой из дуг графа, указаны цифры слагаемых; в знаменателе – результат суммирования в текущем разряде. Сумматор позволяет суммировать двоичные последовательности произвольной длины.

1.4. Поведение изолированного синхронного автомата

Изолированный автомат – автомат, на входе которого присутствует сигнал, имеющий постоянное значение, что эквивалентно "отключению" входа. Если изолированный автомат является синхронным, переходы из одного состояния в другое возможны, но при этом исключены разветвления путей, отображающих последовательности переходов (автомат является детерминированным). Следовательно, автомат с конечным числом состояний (конечный автомат) неизбежно должен попасть в состояние, в котором уже находился ранее, и на диаграммах переходов обязательно будет присутствовать поглощающее состояние или цикл.

Примеры диаграмм, иллюстрирующих поведение рассматриваемого автомата при разных начальных состояниях, приведены рисунке 13.

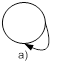
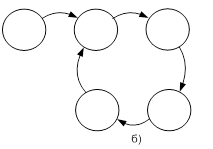
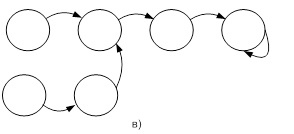
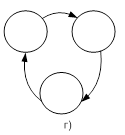
Рис.13. Поведение изолированного синхронного автомата

Отметим, что длина цикла, измеренная числом дуг на диаграмме, не превышает числа состояний (n), то же самое можно сказать и о "времени" вхождения в цикл, измеренном в условных дискретных единицах.

Проблема умножения.

Теорема. Никакой конечный автомат не может перемножать пары чисел
с произвольно большим числом разрядов.

Причина заключается в том, что с возрастанием числа разрядов сомножителей при умножении необходимо накапливать неограниченно большие (по объему занимаемой
памяти) промежуточные результаты.

Для математического доказательства используем метод "от противного": предположим, что существует автомат S, перемножающий пары двоичных чисел с произвольно большим числом разрядов (система счисления может быть любой без ограничения общности). Используем для опровержения последнего утверждения частный случай: оба сомножителя равны 2ⁿ. В этом случае каждый из сомножителей содержит единицу, за которой следуют n нулей; результат умножения (2ⁿ´ 2ⁿ = 2²ⁿ) содержит единицу
и 2 n нулей. Применим экономный способ использования памяти: пары разрядов сомножителей подаются последовательно, начиная с младших разрядов (аналогично тому, как это делалось в рассмотренном выше сумматоре).

Чтобы автомат правильно работал, он должен после прекращения подачи сомножителей добавить к уже выработанным n + 1 нулям еще n – 1 нулей, а затем в заключение единицу. Но после прекращения подачи сомножителей автомат будет работать как изолированный.

Если изолированный автомат S имеет k состояний и способен выработать на выходе подряд n нулей, где n > k, то это означает, что он находится в поглощающем состоянии или вошел в цикл. Следовательно, он уже не сможет выработать единицу. Так как всегда возможно сделать значение n таким, что n – 1 > k, правильный результат при выполнении указанного неравенства не будет получен и, следовательно, предположение о существовании автомата S приводит к противоречию. Теорема доказана.

12 3 4 5 Следующая ⇒

Воспользуйтесь поиском по сайту: