 |
Порождающие грамматики общего типа (ПГОТ)
|
|
|
|
Обозначение грамматики: G = áN, S, P, Sñ,
где:
N – нетерминальный алфавит;
S – терминальный алфавит;
P – множество продукций; т. е. правил вывода вида a – –> β, где α, β Î (N È S)*;
S – аксиома грамматики.
Пример 1. G1 = á{S}, {a, b}, P, Sñ,
где:
P: 1. aSa – –> aSb;
2. S – –> a;
3. S – –> aSa.
Непосредственная выводимость: цепочка β непосредственно выводима из цепочки α в грамматике G, если найдутся такие цепочки γ1, γ2, w1, w2, что α = γ1w1γ2,
β = γ1w2 γ2, и среди правил вывода имеется правило ω1 – –> ω2.
В цепочке α подцепочки γ1, γ2 – контекст. Непосредственно выводимая цепочка получается применением одной продукции грамматики; обозначение непосредственной выводимости: α = => β. Примеры непосредственной выводимости в приведенной грамматике: aSa = => aSb; aSa = => aaa.
Знак «= =>» можно интерпретировать как обозначение бинарного отношения непосредственной выводимости.
Используя понятие непосредственной выводимости, определим выводимость.
Будем записывать: α = =>* β (β выводима из α), если существует последовательность
цепочек α0, α1, α2, …, αn, таких, что α0 = α, αn = β и αi = => αi+1 (i = 0, …, i -1), или
b = a. Указанную последовательность цепочек назовем выводом длины n.
Таким образом, выводимость – рефлексивное и транзитивное бинарное отношение.
В рассмотренной грамматике G1 возможны выводы: S = =>* a (вывод длины 1);
S = =>* aaa (вывод длины 2: S = =>* aSa = =>* aaa).
Язык, порождаемый грамматикой (обозначение – L(G)) – множество терминальных цепочек, выводимых из аксиомы, т. е. L(G) = {z ∊ Σ* | S = =>* z}.
Пример 2. G2 = <N, Σ, P, S>;
N = {A, B, C, S}; S – аксиома;
Σ = {a, b, c};
P: 1. S – –> aSBC;
2. S – –> abC
|
|
|
3. CB – –> BC
4. bB – –> bb
5. bC – –> bc
6. cC – –> cc
Пример вывода: S = => aSBC = => aabCBC = => aabBCC = => aabbCC = =>
= => aabbcC = => aabbcc (здесь правила применены в порядке нумерации).
Грамматика G2 порождает язык L(G) = {an bn cn | n ³ 1}.
Порождающие грамматики общего типа реализуются машинами Тьюринга.
В теории и практике разработки систем программирования, операционных систем, средств синтаксического анализа, компиляции и перевода применяются и другие
грамматики, например, НС-грамматики (грамматики непосредственно составляющих),
КС-грамматики (контекстно-свободные грамматики), А-грамматики (автоматные грамматики).
Все известные грамматики являются частным случаем ПГОТ и получаются посредством ограничений, налагаемых на продукции.
Автоматные грамматики
Порождающая грамматика G = áN, S, P, Sñ называется автоматной, если ее правило вывода имеет следующий вид:
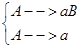- правосторонние правила, или 
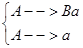- левосторонние правила,
где A, B – элементы нетерминального алфавита; a – элемент терминального алфавита.
Языки, порождаемые А-грамматиками, называются регулярными языками (также языками Клини).
Пример 3: G3 = á{S, A}, {a, b}, P, S>ñ, где приняты правосторонние правила:
P: 1. S – –> aS;
2. S – –> aA;
3. A – –> bA;
4. A – –> b.
Пример вывода: S = = > aS = = > aaA = = > aabA = = > aabb. В общем случае грамматика G3 порождает язык L(G3) = {an bm | n, m > 0}.
А-грамматики маломощны (этот термин характеризует большое в среднем число
шагов при выводе). Тем не менее, существует несложное доказательство того факта, что А-грамматики порождают все возможные конечные языки.
Иллюстрация связи между автоматными грамматиками и автоматами
Рассмотрим правостороннюю А-грамматику G4 = áN, S, P, Sñ:
N = {S1, S2, S3}, где S1 – аксиома; Σ = {x, y, a, b}
P: 1. S1 – –> ybS1
2. S1 – –> xaS2
3. S2 – –> xaS2
4. S2 – –> yaS3
5. S3 – –> xbS1
Правила вывода включают входные терминальные символы x и y и выходные терминальные символы а и b.
|
|
|
Граф автомата Мили, реализующий данную грамматику, приведен на рис. 23.
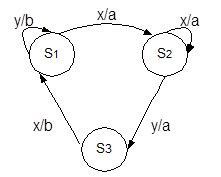
Рис. 23. Граф, реализующий грамматику G4
Рисунок иллюстрирует следующие соответствия:
нетерминалы соответствуют состояниям;
терминалы соответствуют входным и выходным символам;
продукции определяют переходы.
Полученный автомат является преобразователем входных слов в выходные. Так, слово 'yxyx' преобразуется в слово 'baab'. Множество выходных слов образует язык, который порождается данной грамматикой.
Взаимодействие автомата со средой
В теории автоматов значительное место занимали экспериментальные методы:
исследование "поведения" автоматов на моделях, отражающих взаимодействие автоматов с различными видами внешней среды, имеющей дискретное, в частности, автоматное описание.
 |
x(t) x(t) y(t) y(t)
Среду Е можно рассматривать как детерминированный или стохастический автомат, поведение которого зависит от его внутреннего состояния, внешних сигналов и времени.
Введем следующие обозначения:
y(t) – действия автомата;
х(t) – реакция среды;
х(t)= +1 – благоприятная реакция (выигрыш);
х(t)= -1 – неблагоприятная реакция (проигрыш).
В стационарной среде каждое действие автомата вызывает с вероятностью pm значение реакции х(t)= -1 и с вероятностью qm значение х(t)= +1. При этом, qm = 1 - pm;
bm = qm - pm – оценка математического ожидания выигрыша за действие ym.
Принято считать, что автомат обладает целесообразным поведением, если на множестве экспериментальных результатов (при различных соотношениях параметров qm и pm) математическое ожидание выигрыша М > М0, где М0 – математическое ожидание выигрыша при qm = pm = 0,5.
Исторически сложились такие направления исследований с применением моделирования:
Поведение автоматов в детерминированных и случайных средах.
Игры автоматов.
Коллективное поведение автоматов.
Клеточные автоматы.
Большую роль в развитии фундаментальной теории автоматов сыграли такие исследователи, как Дж.фон Нейман, К. Шеннон, М. Л. Цетлин, В. М. Глушков, М. Минский.
Подходящим руководством для первоначального изучения теории формальных грамматик является книга М. Гросса и А. Лантена [4].
|
|
|
|
|
|
