 |
Преобразование автомата Мили в автомат Мура
|
|
|
|
При этом преобразовании в графе автомата Мили не должно быть вершин, в которые не входит ни одна дуга, но которые в то же время имеют хотя бы одну выходящую дугу.
SA = (XA, QA, YA, δA, λA, q1A) – исходный автомат Мили;
SB = (XB, QB, YB, δB, λB, q1B) – целевой автомат Мура.
Для алфавитов автомата SB будут справедливы следующие равенства:
XB = XA,
YB = YA.
Для определения множества QB каждому состоянию qs Î QA поставим в соответствие множество Qs всевозможных пар вида (qs, yt), где yt – выходной сигнал, приписанный дуге, входящей в qs.(фрагмент графа изображен на рис. 28).
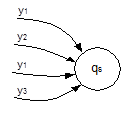
Рис. 28. Вершина qs с входящими дугами
В этом случае Qs представляет собой множество пар вида:
Qs = {(qs, yl), (qs, y2), (qs, y3)}
В общем виде, если D – множество дуг, входящих в вершину qs, то Qs определяется следующим образом:
Qs = {(qs, yt)| yt Î D}
Итак, число элементов Qs равно числу различных выходных сигналов при дугах
автомата SA, входящих в состояние qs. Множество состояний автомата SB получим как теоретико-множественное объединение множеств Qs, ассоциированных со всеми состояниями qs исходного автомата.
Вывод: число состояний в автомате Мура в среднем больше, чем число состояний в автомате Мили.
Функция λB определяется так: каждому состоянию автомата SB, представляющему собой пару (qs, yt), ставится соответствие выходной сигнал yt .
Функция δB определяется следующим образом: если в автомате Мили SA есть переход δA(qi, xj) = qs и при этом выдается выходной сигнал λA(qi, xj) = yp, то в автомате Мура SB будет переход из множества Qi состояний, порожденных состоянием qi, в состояние (qs, yp) под воздействием входного сигнала xj (рис. 29).

Рис. 29. Преобразование автомата Мили в автомат Мура
В качестве начального состояния q1B можно взять любое состояние из множества Q1, порожденного состоянием q1A.
|
|
|
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Дать рекурсивное определение цепочки над некоторым алфавитом, используя понятия пустой цепочки и конкатенации.
2. На вход конечного автомата подается последовательность из нулей и единиц. Изобразить граф, описывающий поведение распознающего автомата, и записать регулярное выражение для распознаваемой последовательности для случаев:
а) число единиц делится на 3;
б) все единицы появляются сериями не менее чем из трех единиц;
в) единица не появляется в момент времени, делящийся на 2 или 3.
3. Заменить регулярное выражение (a Ú b)* таким, в котором не используется
знак "Ú".
4. Совпадают ли множества последовательностей, представляемые регулярными выражениями
а) b(ab Ú b)*a и bb*a(bb*a)*;
б) (a*ab Ú ba)*a* и (a Ú ab Ú ba)*?
5. Какие из следующих равенств верны:
а) E*F = (E Ú E*)*F;
б) E*F* = (E Ú F)*(EF)*;
в) E*F* = E*EF* Ú E*FF*;
г) E(FGE)*FG = EF(GEF)*G?
Здесь E, F, G – метасимволы, обозначающие определенные последовательности символов алфавита.
6. Какие из следующих множеств последовательностей могут быть распознаны конечным автоматом:
а) множество всех последовательностей: 0, 1, 00, 01, 10, 11, 000, 001, 010, …;
б) числа 1, 2, 4, 8, …, 2n, …, записанные в двоичной системе счисления;
в) то же самое множество чисел, записанных в унарном коде: 1, 11, 1111, 11111111,
1111111111111111, …;
г) множество последовательностей, в которых число нулей равно числу единиц;
д) последовательности: 0, 101, 11011, …, 1k01k (k – число повторений единицы)?
Литература
Минский М. Вычисления и автоматы. – М.: Мир, 1971.- 364 с.
Карпов Ю. Г. Теория автоматов. – СПб.: Питер, 2002.- 206 с.
Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. – М.: Энергия, 1986.- 336 с.
Гросс М., Лантен А. Теория формальных грамматик. – М.: Мир, 1971.- 290 с.
Горбатов В. А. Основы дискретной математики. – М.: Высш. школа, 1984.- 310 с.
|
|
|
Романов Владимир Федорович
При написании настоящего учебного пособия использовались конспекты лекций
автора, подготовленные студентами Власенко В. В., Владимировой Н. В.
[1] Иначе говоря, представимо.
[2] Алгоритмом в современной терминологии
|
|
|


