Элементы теории формальных грамматик и языков

Основные определения

Алфавит – множество символов, например, S = {a, b, c,…, z}.

Цепочка (слово) – последовательность символов из алфавита. Для обозначения цепочек используются строчные буквы латинского алфавита: α, β, γ …, а сами цепочки заключаются в ординарные кавычки. Например, S = {a, b, c, =, –, +} – алфавит,
α = ‘a + b = c’– цепочка над алфавитом; п устая цепочка ε = ' ' – цепочка, не содержащая символов.

Рекурсивное определение цепочки над алфавитом S:

БАЗА: ε – цепочка;

    РЕКУРСИЯ: если x Î S и А – цепочка, то Ах – цепочка (здесь A – метасимвол, обозначающий любую цепочку);

ОГРАНИЧЕНИЕ: других цепочек нет.

Длина цепочки – число символов в цепочке, заключается в прямые скобки, например, |α| = 5, |ε| = 0.

Подцепочка: цепочка β является подцепочкой цепочки α, если существуют такие цепочки γ и δ, быть может, пустые, что α = γ β δ.

Цепочка ‘победа’ содержит подцепочки: 'обед', 'беда', 'еда', 'да' (здесь цепочки заданы над алфавитом русского языка).

Конкатенация – сцепление цепочек; обозначается αβ или α·β. Конкатенация ассоциативна, но не коммутативна.

Обозначим через S* – множество всех цепочек над алфавитом S.

Система  {S *, · } образуют известную алгебру – полугруппу, в которой S* - носитель алгебры, · – ассоциативная бинарная операция.

Обращение цепочки. Цепочка β называется обратной цепочкой цепочки α, если она представляет собой последовательность символов цепочки α, выписанных в обратном порядке.

Формальный язык

Формальным языком L на алфавите S называется любое подмножество множества S* (L  S*).

Примеры:

1)некоторыеязыки программирования, например, АЛГОЛ (с рядом оговорок);

2)S = {0, 1}, L = {α |, |α| 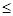 100} – множество цепочек в двоичном алфавите, длина которых не превышает 100 символов;

3)L = {ε} – пустой язык;

4)L = S*;

    5)S = {a, b, c}, α = {aⁿ bⁿ cⁿ | n 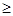 1}, здесь условный показатель n при символе – число повторений символа.

Операции над языками. Поскольку языки – множества, к ним применимы известные теоретико-множественные операции, в частности, объединение языков (L₁ È L₂) и пересечение языков (L₁ Ç L₂).

Специфическая операция – к онкатенация языков:

Пусть L₁ – язык на S₁ и L₂ – язык на S₂, тогда конкатенация языков имеет вид:

L₁ · L₂ = {α β | α Î L₁, β Î L₂}

 

Способы задания языков:

1.Способ перечисления элементов; в искусственных языках не всегда удобен
из-за возможного большого числа элементов.

2.Способ задания с помощью характеристического свойства:

L = {α | Р(α)}, где Р(α) – предикат (характеристическое свойство множества).

Способ задания языка не должен ограничивать длину элемента, входящего в язык. В теории формальных грамматик известны методы определения языков, свободные от указанного ограничения. Выделим два наиболее важных метода.

Задание языков помощью допускающих (распознающих) автоматов.

Задание языков с помощью порождающих грамматик.

Распознающий автомат выделяет из цепочек (слов), подаваемых на его вход, слова, принадлежащие определяемому языку.

Распознающий автомат

     

 

входное слово                                  да (нет)

                                                                                           

 

Порождающая грамматика генерирует "правильные" цепочки, принадлежащие языку L.

 

                                                               Генерирование цепочек языка

 

Далее предметом нашего рассмотрения будут порождающие грамматики.

Компонентами порождающих грамматик являются:

Два алфавита:

- вспомогательный (нетерминальный);

- основной (терминальный).

   Эти два алфавита не содержат общих символов, их пересечение пусто.

Множество правил вывода (продукций), состоящее из упорядоченных пар цепочек áα, βñ. Каждая цепочка в этих парах составлена из объединения элементов терминального и нетерминального алфавитов. Сама продукция обозначается α – –> β и подразумевает замену при подходящих условиях цепочки α цепочкой β.

Начальный символ (аксиома) грамматики – один из нетерминалов, который наделен особым статусом – с него начинается порождения языка.

Примем соглашение, касающееся обозначений в формальных грамматиках:

малыми буквами начала латинского алфавита (a, b, c, …) обозначаются терминалы;

большими буквами начала латинского алфавита (A, B, C, …) обозначаются нетерминалы;

большими буквами конца латинского алфавита (U, V, W, X, Y, Z) обозначаются как терминалы, так и нетерминалы;

греческими буквами (α, β, γ, …) обозначаются цепочки, которые состоят как из терминалов, так и нетерминалов;

малыми буквами конца латинского алфавита (u, v, w, …) обозначаются цепочки, состоящие только из терминалов: именно они являются целевыми.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: