Задачи, приводящие к дифференциальным уравнениям.

Дифференциальные уравнения первого порядка

Дифференциальные равнения являются математической моделью многочисленных физических, химических, биологических и др. процессов. При составлении дифференциальных уравнений весьма часто используют физические законы, которые описывают соотношение между величинами, характеризующими изучаемый процесс, и скоростью изменения этих величин. Например, в механике – законы Ньютона, в теории электрических цепей – законы Кирхгоффа, в теории скоростей химических реакций – закон действия масс и т.д. Если физический закон протекания процесса неизвестен, то для составления дифференциального уравнения прибегают к гипотезе о линейности процесса “в малом”, т.е., например, считают, что в течение малого промежутка времени ∆t участвующие в процессе величины изменяются с постоянной скоростью. Составляют соотношения между приращениями этих величин и, переходя к пределу при ∆t → 0, получают уравнение, содержащее производную по времени. Дифференциальное уравнение – это как бы “мгновенный снимок процесса” в данный момент времени, интегрируя дифференциальное уравнение, мы по мгновенным снимкам восстанавливаем течение процесса в целом.

Задача 1. Пусть в резервуаре имеется a кг водного раствора соли, в котором содержится b кг соли. В определенный момент включается устройство, непрерывно подающее в резервуар с кг чистой воды в секунду и одновременно удаляющее из него ежесекундно с кг раствора

 

При этом в самом резервуаре жидкость непрерывно перемешивается. Как изменяется количество соли в резервуаре?

Примем за начало отсчета момент t. Пусть y(t) – искомая функция, выражающая в каждый момент времени t количество соли в резервуаре. В силу условия задачи и соглашения об отсчете времени,y(0)=b. За малый промежуток [t,t+Dt] из резервуара с раствором выльется (y(t)-(y(t+Dt))) кг соли. Так как концентрация в рассмотренный промежуток времени убывала от до ,то

 

причем неравенства являются строгими, если c¹0, b¹0, разделив это неравенство на Dt, получим

 

 

Исходя из характера рассматриваемого процесса можно заключить, что y(t) – непрерывна, значит,

 

 

В результате получаем

 

т. е. y(t) удовлетворяет дифференциальному уравнению

С учетом начального условия y(0)=b решение этого уравнения имеет вид

Полученная формула показывает, что процесс опреснения раствора в резервуаре происходит по экспоненциальному закону.

Таким образом, дифференциальное уравнение, моделируя процесс описывает эволюцию процесса, показывает характер происходящих с материальной системой изменений.

При этом не обязательно изменения происходят во временном промежутке.

Задача 2. При определении давления воздуха над уровнем моря в зависимости от высоты p(h) поступают следующим образом. Рассматривают два горизонтальных сечения столба воздуха на высоте h и h+Dh, опирающегося на площадку размером 1м². Давление на высоте h+Dh будет меньше на величину Dp, равную весу воздуха в

столбе между двумя сечениями: Dp=dDh, где d – вес одного кубометра воздуха при давлении p. Полагая, что во всех сечениях между h и h+Dh давление постоянно в силу закона Бойля – Мариотта, получают d=kp, где k – коэффициент пропорциональности. Выполняя деление на Dh в равенстве Dp=-kpDh и переходя к пределу при Dh®0, получают дифференциальное уравнение

 

.

 

Приведем еще один пример использования физического закона при составлении дифференциального уравнения.

Пусть требуется узнать, за какое время упадет на поверхность Луны камень с высоты h. Пусть x(t) – высота камня над поверхностью в момент времени t. Согласно закону свободного падения, открытому г. Галилеем, все тела, независимо от их массы, падают в поле силы тяжести с постоянным ускорением a, (для поверхности луны а=1/6g), а следовательно, х¢¢(t)= –а. Интегрируя дважды, находим

 

 

 

Постоянные С₁, С₂ находим из условий х¢(0)=0, и х(0)=h. Функция х(t) = h-at²/2 описывает закон движения камня. Моменту удара t камня о поверхность соответствует x(t)=0, поэтому ответ задачи .

 

Основные понятия теории дифференциальных уравнений.

Обыкновенным дифференциальным уравнением называется уравнение, в котором неизвестной является функция одного независимого переменного, причем в уравнения входят производные различных порядков. В самом общем виде обыкновенное дифференциальное уравнение может быть записано так:

 

 

Порядок старшей производной, входящей в состав уравнения, называется порядком уравнения. Решением уравнения (2.1) называется функция у=ф(х), обращающая это уравнение в тождество. График решения на плоскости ХОУ называется интегральной кривой, процесс нахождения решений – интегрированием дифференциального уравнения.

Уравнение 1-го порядка, разрешенное относительно производной, входящей в состав уравнения, может быть записано в виде

 

(2.1)

 

где f(t,x) – известная функция, определенная в некоторой области D плоскости t,x. Уже на простейших примерах видно, что любое дифференциальное уравнение имеет бесчисленное множество решений. Описать совокупность всех решений позволяет теорема существования и единственности.

Теорема. Если функция f(t,x) и ее частная производная непрерывны в некоторой области D переменных t,x, содержащей точку (t_o,X_o), то существует единственное решение этого уравнения, х=ф(t), удовлетворяющее условию X(t_o)=X_o.

Условие X(t_o)=X_o называется начальным условием, а задача отыскания решения дифференциального уравнения (2.1), удовлетворяющего начальному условию – начальной задачей или задачей Коши.

Геометрически теорема существования и единственности означает, что через каждую точку области проходит одна и только одна интегральная кривая, имеющая в каждой своей точке касательную, целиком принадлежащую области D.

Геометрическая интерпретация самого уравнения (3.1) дает поле направлений в области D, которое получается, если через каждую точку (t,x), принадлежащую области D, провести отрезок l_tx малой длины с угловым коэффициентом f(t,x). Любая интегральная кривая в каждой своей точке касается отрезка l_tx.

На рисункe1 представлено поле направлений уравнения Риккати х'= t²+x², неразрешимого в квадратурах. Рисунок 1 позволяет ясно представить, как должны выглядеть интегральные кривые.

 

 

Рис.1

 

Общим решением дифференциального уравнения (3.1) называется функция Х=Ф(t,C), зависящая от одной произвольной постоянной С, удовлетворяющая дифференциальному уравнению при любом С и такая, что при любом начальном условии X(t_o) = Х_о существует значение С=С_о что Х =Ф(t,C_o) удовлетворяет начальному условию.

Равенство вида Ф(x,t,C)=0, неявно задающее решение, называется общим интегралом дифференциального уравнения. Частным решением называется любая функция у=ф(х,С_о), получающаяся из общего решения при С=С_о. Соотношение Ф(x,t,C_o) = О называется частным интегралом.

Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением. Особое решение

не может быыть получено из общего решения с помощью подбора числа С.

Геометрически особая интегральная кривая - это огибающая семейства интегральных кривых дифференциального уравнения, определяемого его общим интегралом, т.е. кривая которая в каждой своей точке касается некоторой кривой семейства.

 

Метод изоклин

Рассмотрим более подробно применение геометрического подхода к построению решений дифференциальных уравнений первого порядка.

Уравнение

y’ = f(x, y) (3.1)

 

определяет в каждой точке (x, y), где существует функция f(x, y), значение y’, т. е. угловой коэффициент касательной к интегральной кривой в этой точке.

Если в каждой точке области D задано значение некоторой величины, то говорят, что в области D задано поле этой величины.

Таким образом, дифференциальное уравнение (3.1) определяет поле направлений.

Тройка чисел (x, y, y’) определяет направление прямой, проходящей через точку (x, y). Совокупность отрезков этих прямых дает геометрическую картину поля направлений.

Задача интегрирования дифференциального уравнения (3.1) может быть теперь истолковано так: найти такую прямую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.

Задача построения интегральной кривой часто решается с помощью метода изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным прямым имеют одно и тоже направление. Семейство изоклин дифференциального уравнения (3.1) определяется уравнением

 

f(x, y) = k, (3.2)

 

где k – параметр. Строя достаточно густую сеть изоклин, т.е. давая k близкие числовые значения, мы можем достаточно точно построить интегральную кривую дифференциального уравнения (3.1).

З а м е ч а н и е 1. Нулевая изоклина f(x, y) = 0 дает уравнение линий, на которых могут располагаться точки максимума и минимума интегральных кривых. Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят y’’ в силу уравнения (3.1)

 

 

и приравнивают ее нулю. Линия, определяемая уравнением

 

 

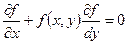
и есть геометрическое место точек перегиба, если они существуют.

 

З а м е ч а н и е 2. Точки пересечения двух или нескольких изоклин являются особыми точками дифференциального уравнения (3.1), так как. в них направление интегральных кривых становится неопределенным.

Например, рассмотрим уравнения . семейство изоклин определяется уравнением . Это семейство прямых, проходящих через начало координат, т. е. В начале координат, пересекаются изоклины, отвечающие различным наклонам касательных к интегральным кривым. Не трудно убедится, что общее решение данного уравнения имеет вид

y = Cx и точка (0, 0) является особой точкой дифференциального уравнения. Здесь изоклины являются интегральными кривыми уравнения (рис. 2).

 

Пример 1. С помощью изоклин построить приближенно интегральные кривые дифференциального уравнения y’ = 2x – y.

 

Р е ш е н и е. Для получения уравнения изоклин положим y’ =k (k = const). Имеем

 

2x – y = k или y = 2x – k.

 

 

рис. 2

 

 

Изоклинами являются параллельные прямые. При k=0 получим изоклину y = 2x. Эта прямая делит плоскость XOY на две части, в каждой из которых производная y’ имеет один и тот же знак (рис. 3).

Интегральные кривые, пересекая прямую y = 2x, переходят из области убывания функции y(х) в область

возрастания, и наоборот, а значит, на этой прямой находятся точки экстремума интегральных кривых, именно точки минимума.

Возьмем еще две изоклины:

 

k = -1, y = 2x +1 и k = 1, y = 2x – 1.

 

Касательные, проведенные к интегральным кривым в точках пересечения с изоклинами k = -1 и k = 1, образуют с осью OX углы в 135^о и 45^о соответственно. Найдем далее вторую производную

 

y’ = 2 – y’ = 2 – 2x +y.

 

Прямая y = 2x –2, на которой y’’ = 0, является изоклиной, получаемой при k =2, и в тоже время интегральной линией, в чем можно убедиться подстановкой в уравнение. Так как правая часть данного уравнения f(x, y) = 2x – y удовлетворяет условиям теоремы существования и единственности во всей плоскости XOY, то остальные интегральные кривые не пересекают эту изоклину. Изоклина y = 2x, на которой находятся точки минимума интегральных кривых, расположена над изоклиной y = 2x – 2, а по этому интегральные кривые, проходящие ниже изоклины y = 2x – 2, не имеют точек экстремума.

Прямая y = 2x – 2 делит плоскость XOY на две части, в одной из которых (расположенной над прямой) y²>0, а значит, интегральные кривые обращены вогнутостью вверх, а в другой y” <0 и значит, интегральные кривые обращены вогнутостью вниз. Так как. интегральные кривые не пересекают прямой y = 2x – 2, то она не является геометрическим местом точек перегиба. Следовательно, интегральные кривые данного уравнения не имеют точек перегиба.

Проведенное исследование позволяет нам приближенно построить семейство интегральных кривых уравнения (рис. 3).

 

 

Рис.3

 

Рассмотрим простейшие и наиболее распространенные в приложениях случаи, когда уравнение (3.1) интегрируемо в квадратурах.

 

 

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: