 |
Уравнения, неразрешенные относительно производной
|
|
|
|
Общего метода решения уравнений, неразрешимых относительно производной, нет. Если дифференциальное уравнение Р(х,у,у¢) = 0 разрешимо либо относительно искомой функции у = f(x.y'), либо относительно аргумента х = f(y,y¢), то оно может быть проинтегрировано путем введения параметра р = у'. Исходное уравнение перейдет в алгебраическое, дифференцируя соответственно по х или по у, получим системы уравнений
 или
или 
решения которых находятся в явном иди параметрическом виде.
Рассмотрим, например, уравнение Лагранжа
у = xf(y')+j(y').
Введением параметра р=у' уравнение Лагранжа приводится к виду у = хf(р)+j(р). Дифференцируя по х, получим

или, после замены у' через р и алгебраических преобразований,

Это линейное уравнение относительно х и производной  .
.
Его общий интеграл имеет вид Ф(х,р,С)=0. Совместно с уравнением
у = xf(y')+j(у)
он дает общий интеграл уравнения Лагранжа. Произведенное преобразование возможно лишь, если р-f(р)¹0. Корни уравнения p-f(p)=0 дадут также решения уравнения Лагранжа, это особое решение, представляющее собой прямую линию. К уравнениям, не разрешенным относительно производной, приводят чаще всего различные геометрические задачи такие, как задачи об изогональных траекториях и др.
Пример 1:
Найти общий интеграл уравнения: 
Решение:
Разлагая левую часть уравнения на множители получим: 
откуда  и
и  . Оба эти уравнения являются уравнениями с разделяющимися переменными. Их общие интегралы:
. Оба эти уравнения являются уравнениями с разделяющимися переменными. Их общие интегралы:
 ,
,  .
.
Поэтому общий интеграл исходного уравнения имеет вид: 
Пример 2:
Найти общее решение уравнения  в параметрической форме.
в параметрической форме.
Решение: Положим  ; тогда
; тогда  . Равенство
. Равенство 
перепишем в форме  , так как
, так как
|
|
|
 ]
]

то, следовательно,  . Общее решение запишется так:
. Общее решение запишется так:

Пример 3:
Найти общее решение уравнения  .
.
Решение:
Положим  ; тогда
; тогда  . Из равенства
. Из равенства  находим
находим  . Та как
. Та как 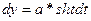 , то
, то  и
и  . В параметрической форме общее решение запишется так:
. В параметрической форме общее решение запишется так:

Исключим параметр p. Для этого из первого уравнения находим t и подставляем во второе. Имеем  и
и  .
.
Пример 4:
Найти общее решение уравнения: 
Решение:
Положим, что  . Тогда
. Тогда  , или
, или  . Продифференцировав по x, имеем
. Продифференцировав по x, имеем
 .
.
После несложных преобразований получим  , или
, или
 Произведя потенцирование, находим:
Произведя потенцирование, находим:  . Следовательно, общее решение в параметрической форме примет вид:
. Следовательно, общее решение в параметрической форме примет вид:

Исключим параметр p. Для этого найдем выражение
ти подставим в уравнение  . Таким образом, общее решение
. Таким образом, общее решение  .
.
Пример 5:
Найти общее решение уравнения  , где
, где  .
.
Решение:
Общее решение получаем непосредственно из уравнения заменой p на C: 
Для получения особого решения найдем  Система уравнений
Система уравнений

представляет собой особое решение в параметрической форме.Исключим параметр p. Для этого возведем обе части второго уравнения в квадрат и разделим их на соответствующие части первого уравнения; получим  , откуда
, откуда  . Геометрически общее решение представляет собой однопараметрического семейство прямых
. Геометрически общее решение представляет собой однопараметрического семейство прямых  , а особый интеграл параболу.
, а особый интеграл параболу.

Рис.4
Непосредственно из чертежа видно, что особый интеграл (парабола) оказался геометрически огибающей семейства интегральных линий (прямых), определяемых общим решением. Это свойство не случайно.
Возможность существования особых решений связана с нарушением условий теоремы Коши Как мы знаем, выполнение этих условий гарантирует существование и единственность решений – не может быть двух различных решений, удовлетворяющих одному тому же начальному условию. Были рассмотрены случаи, когда эти условия нарушались только в отдельных особых точках. Между тем условия единственности могут нарушаться во всех точках некоторой линии, которая сама может оказаться решением уравнения. Это решение и называют особым.
|
|
|
|
|
|


