 |
Линейные однородные уравнения высших порядков
|
|
|
|
Дифференциальное уравнение называется линейным, если неизвестная функция и все ее производные входят в уравнение линейно. Линейное дифференциальное уравнение порядка n имеет вид

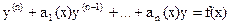
Уравнение называется однородным, если f(x)º0, если f(x)º0,то уравнение называется неоднородным. Всякое решение линейного уравнения является частным, особых решений линейное уравнение не имеет.
Линейная комбинация решений однородного линейного уравнения является также решением однородного линейного уравнения. Если известно какое-либо частное решение у1(х) однородного уравнения, то подстановка у(х)=у1(х)z(х
приводит это уравнение к линейному уравнению относительно функции z(x), несодержащему явно эту функцию. Поэтому, полагая z'(х) = u(х), получаем линейное однородное уравнение порядка n-1 относительно функции u(х). Однако общих методов отыскания частных решений линейных однородных уравнений с коэффициентами, зависящими от переменной х, нет.
Система функций у1(х),у2(х),...,уn(х) линейно независима на интервале (а,b), если определитель Вронского этой системы
W(x)= 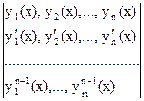
отличен от нуля хотя бы в одной точке хÎ(а,b).
Всякая система из n линейно независимых решений 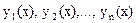 называется фундаментальной системой решений этого уравнения. Если известна фундаментальная система решений уравнения, то общее решение этого уравнения имеет вид
называется фундаментальной системой решений этого уравнения. Если известна фундаментальная система решений уравнения, то общее решение этого уравнения имеет вид
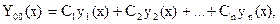
где С1, С2,...,Сn- произвольные постоянные. Общее решение неоднородного дифференциального уравнения находят как сумму общего решения однородного и некоторого частного решения неоднородного уравнения. Если известно общее решение у00(х), то для определения частного решения можно воспользоваться методом вариации произвольных постоянных.
|
|
|
Рассмотрим ЛНДУ
y″ + a(x)y' + a2(x)y = f(x) (3.1)
Его общим решением является функция
y = y*+ y° (3.2)
Частное решение у* уравнения (3.1) можно найти, если известно общее решение у° соответствующего однородного уравнения
y″ + a(x)y' + a2(x)y =0 (3.3)
методом вариации произвольных постоянных (метод Лагранжа), состоящим в следующем.
Пусть y° = c1y1(x) + c2y2(х) — общее решение уравнения (3.3).
Заменим в общем решении постоянные c1 и c2 неизвестными функциями c1(x) и с2(х) и подберем их так, чтобы функция
y* = с1(х)у1(х) + с2(х)у2(х) (3.4)
была решением уравнения (3.1). Найдем производную
(y*)' = с1´(х) у1(х) + с1(х)у1'(х) + с2'(х)у2(х + с2(х)у2'(х)
Подберем функции c1(x) и с2(х) так, чтобы
с1´(х)у1(х) + с2'(х)у2(х) = 0 (3.5)
Тогда
(y*)' = с1(х)у1'(х) + с2(х)у2'(х),
(y*)″ = с1´(х)у1'(х) + с1(х) у1″(х) + с2'(х)у2'(х) + с2(х)у2″(х).
Подставляя выражение для у*, (у*)' и (у*)" в уравнение (3.1), получим:
с1´(х)у1'(х) + с1(х) у1″(х) + с2'(х)у2'(х) + с2(х)у2″(х) +
+ a(x)[с1(х)у1'(х) + с2(х)у2'(х)] +
+ а2(x)[ с1(х)у1(х) + с2(х)у2(х)] =f(x)
или
с1(х)[ у1″(х) + a(x) у1'(х) + а2(x) у1(х)] + с2(х)[ у2″(х) + a(x) у2'(х) +
а2(x) у2(х)] + с1´(х)у1'(х) + с2'(х)у2'(х) = f(x).
Поскольку у1(х) и у2(х) — решения уравнения (3.2), то выражения в квадратных скобках равны нулю, а потому
с1´(х)у1'(х) + с2'(х)у2'(х) = f(x) (3.6)
Таким образом, функция (3..4) будет частным решением у* уравнения (3.1), если функции c1(x) и с2(х) удовлетворяют системе уравнений (3..5) и (3.6):
c1´(х)у1(х) + с2'(х)у2(х) = 0,
с1´(х)у1'(х) + с2'(х)у2'(х) = f(x) (3.7)
Определитель данной системы не равен нулю, так как это определитель Вронского для фундаментальной системы частных решений у1(х) и у2(х) уравнения (3.3).
Поэтому система (2.2.9) имеет единственное решение: с1´(х) = φ(x) и с2'(х) = φ2(x), где φ(x) и φ2(х) — некоторые функции от х. Интегрируя эти функции, находим с1(х) и с2(х), а затем по формуле (3.4) составляем частное решение уравнения (3.1).
|
|
|
Пример 1. Решить уравнение 
Решени е. Соответствующее однородное уравнение будет  Его характеристическое уравнение
Его характеристическое уравнение 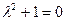 имеет мнимые корни l1= -i, l2= i и общее решение однородного уравнения имеет вид:
имеет мнимые корни l1= -i, l2= i и общее решение однородного уравнения имеет вид:
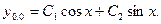
Общее решение исходного уравнения ищем в виде
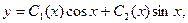 (А)
(А)
где C1 (x) и C2 (x) – неизвестные функции от x. Для их нахождения составим систему:
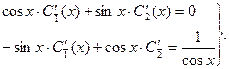
Разрешаем эту систему относительно 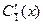 и
и  :
:

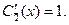
Откуда интегрированием находим:
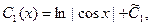
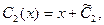
Подставляя выражения C1(x) и C2(x) в (А), получим общий интеграл данного уравнения
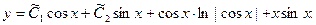
Здесь  есть частное решение исходного неоднородного уравнения.
есть частное решение исходного неоднородного уравнения.
|
|
|


