Элементы теории устойчивости

 

Предварительные замечания

 

Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных.

 

(1.4)))1)

 

x(t₀)=x₀

 

Если функция f(t,x) непрерывна по совокупности аргументов и имеет ограниченную производную дf/дх в некоторой области W изменения t, x, содержащей точку (t_о, x_o), то решение задачи Коши существует и единственно. Если изменять значения t₀ и x₀, то будет меняться и решение. Возникает важный в приложениях вопрос: как оно будет при этом меняться? Вопрос этот имеет и большое принципиальное значение. Действительно, если какая-либо физическая задача приводит к задаче Коши, то начальные значения находятся из опыта и за абсолютную точ­ность измерения ручаться нельзя. И если сколь угодно малые изменения начальных данных способны сильно изменять решение, то математическая модель окажется мало пригодной для описания реального процесса.

Справедлива следующая теорема о непрерывной зависимости решения от начальных условий

4.3

Теорема 4.1. Если правая часть f(t, x) дифференциального уравнения

dx/d t= f(t, x) (1.4)

 

непрерывна по совокупности переменных и имеет ограниченную частную производную дf/дх в некоторой области G изменения t, x, то решение x(t)==x(t, t_o, х_o), удовглетворяющее начальному условию x(t₀)=x₀, где (t_0,x₀)ÎG, непрерывно зависит от начальных данных.

 

- 76 -

 

Иными словами, пусть через точку (t_0,x₀) проходит решение x(t)

 

уравнения (1.4), определенное на отрезке a£t£b, t₀Î(a,b). Тогда

 

для любого e>0 найдется такое 6>0, что при <d, <d

 

решение уоравнения (4.3), проходящее через точку 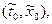, существует на отрезке [a,b] и отличается там от x(t) меньше чем на e

 

 

Аналогичная теорема справедлива и для системы

дифференциальных уравнений

 

 

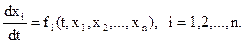
При выполнении условий теоремы (5.1) решение задачи Коши существует, единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача Коши поставлена корректно. Существенным является то обстоятельство, что отрезок [a,b] изменения t конечен. Однако во многих задачах нас интересует зависимость решения от начальных данных в бесконечном промежутке . Переход от конечного промежутка, в котором рассматривается непрерывная зависимость решения от начальных значений, к бесконечному существенно меняет характер задачи и методы исследования. Эта проблема относится к теории устойчивости, созданной А. М. Ляпуновым (см. работу «общественная задача об устойчивости движения» (Гостехиздат, 1980)).

 

- 77 -

 

 

Рассмотрим линейные системы, для которых решение существует для (глобальная теорема существования):

 

 

 

функции a_ij(t) и f_i(t) — непрерывны на . Для таких систем каждое решение существует на (неограниченно продолжаемо вправо) и единственно. Не все системы обладают таким свойством.

)

Например, для скалярного уравнения

 

 

функция f(t, х)ºх² непрерывна и имеет производные всех порядков по х. Нетрудно проверить, что функция х=a/(1 - at) является решением задачи

dx/dt=x², x(0)=a, a>0.

 

Однако это решение существует только в интервале (- , 1/a), зависящем от начального условия, и непродолжаемо на полуинтервал (- , 1/a].

Уравнение (4.4) есть уравнение сверхбыстрого размножения, когда прирост пропорционален числу всевозможных пар. Его решение показывает, что при таком законе прироста населения количество населения становится бесконечным за конечное время (в то время как обычный закон прироста — экспоненциальный).

 

 

- 78 -

 

 

Устойчивость по Ляпунову. Основные понятия, определения

 

Рассмотрим дифференциальное уравнение первого порядка

 

dx/dt=f(t,x); (2.1)

 

где функция f(t,х) определена и непрерывна для и х из некоторой области D и имеет ограниченную частную производную df/dх. Пусть функция есть решение уравнения, удовлетворяющее начальному условию Пусть, далее, функция x=x(t) есть решение того же уравнения, удовлетворяющее другому начальному условию Предполагается, что решения j(t) и x(t) определены для всех t³to, т. е. неограниченно продолжаемы вправо.

Определение. Решение x=j(t) уравнения (5.5) называется устойчивым по Ляпунову при ,если для любого e>0 существует d=d(e)>0 такое, что для всякого решения x=x(t) этого уравнения из неравенства

(5.6)

следует неравенство

5.7

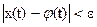
для всех t³to (всегда можно считать, что d£e).

Это значит, что решения, близкие по начальным значениям к решению х=j(t), остаются близкими и при всех t³to.

Геометрически это означает следующее. Решение x=j(t) урав­нения (5.5) устойчиво, если, какой бы узкой ни была e-полоска, содержащая кривую х=j(t), достаточно близкие к ней в начальный

 

момент t=to интегральные кривые x=x(t) уравнения цели­ком содержатся в указанной e-полоске при всех t³to (рис.2).

 

Если при сколь угодно ма­лом 6>0 хотя бы для одного решения x=x(t) уравнения (5.5) неравенство (5.7) не выполняется, то решение х=j(t) этого уравнения называется неустой­чивым.

 

Неустойчивым следует счи­тать и решение, не продолжаемое вправо при .

Определение 5.2. Решение x=j(t) уравнения (5.5) назы­вается асимптотически устойчивым, если

1) решение х = j(t) устойчиво,

2) существует 6₁>0 такое, что для любого решения x=x(t) уравнения (5.5), удовлетворяющего условию 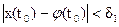, имеем

Это означает, что все решения x=x(t), близкие по начальным условиям к асимптотически устойчивому решению x=j(t), не только остаются близкими к нему при t ³ to, но и неограниченно сближаются с ним при . Вот простая физическая модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения, положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возра­станием времени, т. е. положение равновесия будет асимптотиче­ски устойчивым.

Пример. 1. Исследовать на устойчивость тривиальное решение хº0 уравнения.

dx/df=0. (*)

Решение хº0, очевидно, удовлетворяет начальному условию . Решение уравнения (*), удовлетворяющее начальному условию , имеет вид хºх₀. Легко видеть (рис. 5),

 

 

Рис. 5

что, какова бы ни была e-полоска вокруг интегральной кривой х=0, существует d>0, например d=e, такое, что любая интегральная кривая х=х₀, для которой | х₀-0 | <d, целиком содержится в указанной e-полоске для всех t³to. Следовательно, решение хº0 устойчиво. Асимптотической устойчивости нет, поскольку пря­мая х=х₀ при не стремится к прямой х=0.

 

 

Рис. 6

 

Пример 1. Исследовать на устойчивость тривиальное решение хº0 уравнения

dx/dt=-a²x (a==const), (1)

 

решение уравнения (1), удовлетворяющее начальному условию , имеет вид

Возьмем любое e>0 и рассмотрим разность решений х(t) и j(t)º0:

 

(***)

Поскольку для всех t³to, из выражения (***) следует, что существует d>0, например d=e, такое, что при |x₀-0|<d=e. имеем

Согласно определению (5.1) это означает, что решение j(t)º0 уравнения (**) устойчиво.

Кроме того, имеем

поэтому решение j (t)º0 асимптотически устойчиво (рис. 6).

Пример 5.3. Показать, что решение j(t)º0 урав­нения

dx/dt=a²x

неустойчиво.

В самом деле, при сколь угодно малом решение этого уравнения не удовлетворяет условию при достаточно больших t>to. Более того, при любых x₀¹0 имеем (рис. 7)

 

..

5.8

Рассмотрим теперь систему дифференциальных уравнений

где функции h определены для из некоторой области D изменения и удовлетворяют условиям теоремы существования и единственности решения задачи Коши. Предположим, что все решения системы (5.8) неограниченно продолжаемы вправо при .

Определение. Решение системы (5.8) называется устойчивым по Ляпунову при для любого e>0 существует d=d(e)>0 такое, что для всякого решения х_i(t) (i=l, 2,..., n) той же системы, начальные значения которого удовлетворяют неравенствам:

выполняются неравенства

5.9

для всех t³t₀ близкие по начальным значениям решения остаются близкими для всех t³t₀.

Если при сколь угодно малом d>0, хотя бы для одного решения x_i(t), i==l, 2,..., n, неравенства (5.9) не выполняются, то решение j_i(t) называется неустойчивым.

Определение. Решение j_i(t), I = 1, 2,..., n, системы (5.8) называется асимптотически устойчивым, если:

1) решение это устойчиво,

2) существует di> 0 такое, что всякое решение x_i(t), i =1, 2,..., n, системы, для которого

удовлетворяет условию

Из устойчивости нетривиального решения дифференциального уравнения не следует ограниченности этого решения. Рассмотрим например, уравнение dx/dt=1. Решением этого уравнения, удовлетворяющим условию x(o)=o, является функция j(t)=t. Решение, удовлетворяющее начальному условию х(0)=x₀, имеет вид x(t)=t+x₀. Геометрически очевидно (рис. 8), что для всякого e>0 существует d>0, например d=e, такое, что любое решение х(t) уравнения, для которого верно неравенство |x₀-0|<d удовлетворяет условию | х (t) - t|<e "t³0.

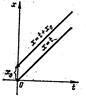
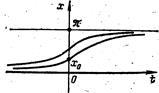
Рис.8 Рис. 9

 

Последнее означает, что решение j(t)=t устойчиво по Ляпунову, однако это решение является неограниченным при .

5.10

Из ограниченности решений дифференциального уравнения не следует устойчивости решений. Рассмотрим уравнение

dx/dt= sin² x.

5.11

Оно имеет очевидные решения

x= kp, k=± 1, ± 2.....

5.12

интегрируя уравнение (5.10), находим ctg х = ctg x₀ - t или

х = arcctg (ctg x₀ – t), x¹kp.

Все решения (5.11) и (5.12) ограничены на (.) Однако решение j(t)º0 неустойчиво при . так как при любом имеем (рис. 9).

Таким образом, ограниченность и устойчивость решений являются понятиями, независимыми друг от друга.

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: