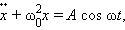Вынужденные колебания. Резонанс. Автоколебания

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω₀.

Если свободные колебания происходят на частоте ω₀, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.

После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.

В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω₀. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.

Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону

y = ym cos ωt.

где y_m – амплитуда колебаний, ω – круговая частота.

Такой закон перемещения можно обеспечить с помощью шатунного механизма, преобразующего движение по окружности в поступательно-возвратное движение (рис. 2.5.1).

Рисунок 2.5.1. Вынужденные колебания груза на пружине. Свободный конец пружины перемещается по закону y = ym cos ωt. l – длина недеформированной пружины, k – жесткость пружины

Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно:

Δl = x – y = x – ym cos ωt.

Второй закон Ньютона для тела массой m принимает вид:

ma = –k(x – y) = –kx + kym cos ωt.

В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.

Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой: Тогда уравнение вынужденных колебаний запишется в виде

(**)

где – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением:

Уравнение (**) не учитывает действия сил трения. В отличие от уравнения свободных колебаний (*) (см. §2.2) уравнение вынужденных колебаний (**) содержит две частоты – частоту ω₀ свободных колебаний и частоту ω вынуждающей силы.

Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону

x (t) = xmcos (ωt + θ).

Амплитуда вынужденных колебаний x_m и начальная фаза θ зависят от соотношения частот ω₀ и ω и от амплитуды <m>m>y_m внешней силы.

На очень низких частотах, когда ω << ω₀, движение тела массой m, прикрепленного к правому концу пружины, повторяет движение левого конца пружины. При этом x (t) = y (t), и пружина остается практически недеформированной. Внешняя сила приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω₀ стремится к нулю.

Если частота ω внешней силы приближается к собственной частоте ω₀, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды x_m вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой (рис. 2.5.2).

При резонансе амплитуда x_m колебания груза может во много раз превосходить амплитуду y_m колебаний свободного (левого) конца пружины, вызванного внешним воздействием. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.

Модель. Вынужденные колебания

У колебательных систем с не очень высокой добротностью (< 10) резонансная частота несколько смещается в сторону низких частот. Это хорошо заметно на рис. 2.5.2.

Явление резонанса может явиться причиной разрушения мостов, зданий и других сооружений, если собственные частоты их колебаний совпадут с частотой периодически действующей силы, возникшей, например, из-за вращения несбалансированного мотора.

Рисунок 2.5.2. Резонансные кривые при различных уровнях затухания: 1 – колебательная система без трения; при резонансе амплитуда xm вынужденных колебаний неограниченно возрастает; 2, 3, 4 – реальные резонансные кривые для колебательных систем с различной добротностью: Q2 > Q3 > Q4. На низких частотах (ω << ω0) xm ≈ ym. На высоких частотах (ω >> ω0) xm → 0

Вынужденные колебания – это незатухающие колебания. Неизбежные потери энергии на трение компенсируются подводом энергии от внешнего источника периодически действующей силы. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколебательными, а процесс незатухающих колебаний в таких системах – автоколебаниями. В автоколебательной системе можно выделить три характерных элемента – колебательная система, источник энергии и устройство обратной связи между колебательной системой и источником. В качестве колебательной системы может быть использована любая механическая система, способная совершать собственные затухающие колебания (например, маятник настенных часов).

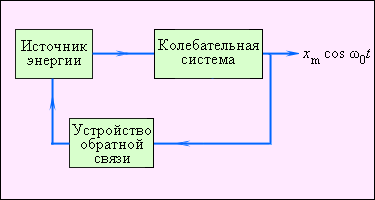
Источником энергии может служить энергия деформация пружины или потенциальная энергия груза в поле тяжести. Устройство обратной связи представляет собой некоторый механизм, с помощью которого автоколебательная система регулирует поступление энергии от источника. На рис. 2.5.3 изображена схема взаимодействия различных элементов автоколебательной системы.

Рисунок 2.5.3. Функциональная схема автоколебательной системы

Примером механической автоколебательной системы может служить часовой механизм с анкерным ходом (рис. 2.5.4). Ходовое колесо с косыми зубьями жестко скреплено с зубчатым барабаном, через который перекинута цепочка с гирей. На верхнем конце маятника закреплен анкер (якорек) с двумя пластинками из твердого материала, изогнутыми по дуге окружности с центром на оси маятника. В ручных часах гиря заменена пружиной, а маятник – балансиром – маховичком, скрепленным со спиральной пружиной. Балансир совершает крутильные колебания вокруг своей оси. Колебательной системой в часах является маятник или балансир. Источником энергии – поднятая вверх гиря или заведенная пружина. Устройством, с помощью которого осуществляется обратная связь, является анкер, позволяющий ходовому колесу повернуться на один зубец за один полупериод. Обратная связь осуществляется взаимодействием анкера с ходовым колесом. При каждом колебании маятника зубец ходового колеса толкает анкерную вилку в направлении движения маятника, передавая ему некоторую порцию энергии, которая компенсирует потери энергии на трение. Таким образом, потенциальная энергия гири (или закрученной пружины) постепенно, отдельными порциями передается маятнику.

Механические автоколебательные системы широко распространены в окружающей нас жизни и в технике. Автоколебания совершают паровые машины, двигатели внутреннего сгорания, электрические звонки, струны смычковых музыкальных инструментов, воздушные столбы в трубах духовых инструментов, голосовые связки при разговоре или пении и т. д.

Рисунок 2.5.4. Часовой механизм с маятником

 

Колебательные процессы широко известны в природе и технике. Природа колебаний и сам колеблющийся объект могут быть различны: температура, атомы твердого тела, центр тяжести маятника, электрическое и магнитное поля и т. д. Среди них особое место занимают механические колебания. К данному виду колебаний можно отнести движение маятников, струн, мембран телефонов, поршней двигателей внутреннего сгорания, мостов и других сооружений, подвергнутых действию переменной силы.

Пример колебательной систеыМеханическим колебанием называется процесс, при котором характеристики движения принимают одни и те же значения через некоторые промежутки времени. Колебания, при которых значения физических величин, описывающих данный процесс, повторяются через равные промежутки времени называются периодическими. Минимальное значение этого промежутка времени называется периодом колебаний.

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: