 |
Свободные колебания. Колебательные системы.
|
|
|
|
| Свободные колебания тела – это колебания, происходящие только благодаря начальному запасу энергии. |
Пояснение.
Отведем в сторону мячик, висящий на нитке, и отпустим его. Мячик начнет совершать колебательные движения влево-вправо. Это и есть свободные колебания.
| Системы тел, которые способны совершать свободные колебания, называютсяколебательными системами. |
Пояснение:
В нашем примере мячик, нитка и устройство, к которому нитка прикреплена, вместе составляют колебательную систему.
Амплитуда, период, частота колебаний.
| Амплитуда – это наибольшее отклонение колеблющегося тела от положения равновесия. Измеряется в метрах, сантиметрах и т.п. |
Пояснение:
Мячик на нитке достигает определенного предела колебания, затем начинает движение в обратную сторону. Расстояние от положения равновесия (покоя) до этой крайней точки и называется амплитудой.
| Период колебаний – это промежуток времени, в течение которого тело совершает одно полное колебание. |
Период колебаний обычно измеряется в секундах.
Обозначается буквой Т.
| Частота колебаний – это число колебаний, совершаемых в единицу времени. |
За единицу частоты принято одно колебание в секунду. Название этой единицы – герц (Гц).
Частота колебаний обозначается буквой ν («ню»).
Пояснение:
Если мячик за одну секунду совершает два колебания, то частота его колебаний составляет 2 Гц. То есть ν = 2Гц.
| Чтобы найти период колебаний, надо одну секунду разделить на частоту колебаний: 1 Т = —— ν |
Пояснение:
В нашем примере мячик за одну секунду совершает два колебания. Такова его частота колебаний. Значит:
1
Т = —— = 0,5 с.
2Гц
|
|
|
| Частота свободных колебаний называется собственной частотой колебательной системы. |
Виды колебаний.
Колебания бывают гармонические, затухающие, вынужденные.
Простейшим видом колебаний являются гармонические колебания — колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
Так, при равномерном вращении шарика по окружности его проекция (тень в параллельных лучах света) совершает на вертикальном экране (рис. 13.2) гармо-ническое колебательное движение.
Смещение от положения равновесия при гармонических колебаниях описывается уравнением (его называют кинематическим законом гармонического движения) вида:
x = A cos(2 πTt + φ 0) или x = A sin(2 πTt + φ ′0)
где х — смешение — величина, характеризующая положение колеблющейся точки в момент времени t относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в заданный момент времени; А — амплитуда колебаний — максимальное смещение тела из положения равновесия; Т — период колебаний — время совершения одного полного колебания; т.е. наименьший промежуток времени, по истечении которого повторяются значения физических величин, характеризующих колебание; φ 0 — начальная фаза; φ =2 πTt + φ ′0 — фаза колебании в момент времени t. Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы (смещение, скорость, ускорение) тела в любой момент времени.
Если в начальный момент времени t0= 0 колеблющаяся точка максимально смещена от положения равновесия, то φ 0=0, а смещение точки от положения равновесия изменяется по закону
x = A cos2 πTt.
Если колеблющаяся точка при t0 = 0 находится в положении устойчивого равновесия, то смещение точки от положения равновесия изменяется по закону
|
|
|
x = A sin2 πTt.
Величину V, обратную периоду и равную числу полных колебаний, совершаемых за 1 с, называют частотой колебаний:
ν =1 T (в СИ единицей частоты является герц, 1Гц = 1с-1).
Если за время t тело совершает N полных колебаний, то
T = tN; ν = Nt.
Величину ω =2 πν =2 πT, показывающую, сколько колебаний совершает тело за 2 π с, называют циклической (круговой) частотой.
Кинематический закон гармонического движения можно записать в виде:
x = A cos(2 πνt + φ 0), x = A cos(ωt + φ 0).
Графически зависимость смещения колеблющейся точки от времени изображается косинусоидой (или синусоидой).
На рисунке 13.3, а представлен график зависимости от времени смещения колеблющейся точки от положения равновесия для случая φ 0=0, т.е. x = A cos ωt.


Рис. 13.3
Выясним, как изменяется скорость колеблющейся точки со временем. Для этого найдем производную по времени от этого выражения:
υx = x ′ A sin ωt = ωA cos(ωt + π 2),
где ωA =| υx | m — амплитуда проекции скорости на ось х.
Эта формула показывает, что при гармонических колебаниях проекция скорости тела на ось х изменяется тоже по гармоническому закону с той же частотой, с другой амплитудой и опережает по фазе смешение на π 2 (рис. 13.3, б).
Для выяснения зависимости ускорения ax(t) найдем производную по времени от проекции скорости:
ax = υ ′ x =− ω 2 A cos ωt = ω 2cos(ωt + π),
где ω 2 A =| ax | m — амплитуда проекции ускорения на ось х.
При гармонических колебаниях проекция ускорения опережает смещение по фазе на к (рис. 13,3, в).
Аналогично можно построить графики зависимостей x (t), υx (t) и ax (t), если x = A sin ωt при φ 0=0.
Учитывая, что A cos ωt = x, формулу для ускорения можно записать
ax =− ω 2 x,
т.е. при гармонических колебаниях проекция ускорения прямо пропорциональна смещению и противоположна ему по знаку, т.е. ускорение направлено в сторону, противоположную смещению.
Так, проекция ускорения — это вторая производная от смещения аx=х' ', то полученное соотношение можно записать в виде:
ax + ω 2 x =0 или x ′′+ ω 2 x =0.
Последнее равенство называют уравнением гармонических колебаний.
Физическую систему, в которой могут существовать гармонические колебания, называют гармоническим осциллятором, а уравнение гармонических колебаний — уравнением гармонического осциллятора.
|
|
|
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 368-370.
Колебаниями называют физические процессы, точно или почти точно повторяются через одинаковые промежутки времени. Колебания бывают механическими и электромагнитными. С колебаниями мы встречаемся не только в технике, но и в природе и жизни человека. Например, колеблется поршень двигателя, листья деревьев, струны музыкальных инструментов, бьется сердце. Главной особенностью колебательного движения является его периодичность.
Существует два вида колебательного движения: свободные и вынужденные колебания.
Свободные колебания — это колебания, которые происходят в механической системе под действием внутренних сил системы после кратковременного воздействия внешних сил.
Система тел, которые могут выполнять свободные колебания, называется колебательной системой.
Для того чтобы существовали свободные колебания, необходимо выполнение двух условий:
1. Система должна находиться около положения устойчивого равновесия.
2. Силы трения должны быть достаточно малыми.
Вынужденные колебания — колебания, возникающие под действием внешних сил, которые изменяются со временем по модулю и направлению.
Характеристики колебательного движения:
— Амплитуда — модуль наибольшего отклонения тела от положения равновесия. Обозначается буквой А и измеряется в метрах.
— Период — минимальный промежуток времени, за который происходит одно колебание. Период обозначается буквой Т и измеряется в секундах.
— Частота — число колебаний за единицу времени. Обозначается буквой ν и измеряется в герцах. Частота обратно пропорциональна периода, поэтому для того чтобы найти частоту, необходимо единицу разделить на период.
|
|
|
— Циклическая частота — число колебаний за 2π секунд. Циклическая частота обозначается буквой ω и измеряется в секундах в минус первой степени. Для того чтобы найти циклическую частоту, надо частоту умножить на 2π.
Основные понятия
 Колебательные процессы широко известны в природе и технике. Природа колебаний и сам колеблющийся объект могут быть различны: температура, атомы твердого тела, центр тяжести маятника, электрическое и магнитное поля и т.д. Среди них особое место занимают механические колебания. К данному виду колебаний можно отнести движение маятников, струн, мембран телефонов, поршней двигателей внутреннего сгорания, мостов и других сооружений, подвергнутых действию переменной силы.
Колебательные процессы широко известны в природе и технике. Природа колебаний и сам колеблющийся объект могут быть различны: температура, атомы твердого тела, центр тяжести маятника, электрическое и магнитное поля и т.д. Среди них особое место занимают механические колебания. К данному виду колебаний можно отнести движение маятников, струн, мембран телефонов, поршней двигателей внутреннего сгорания, мостов и других сооружений, подвергнутых действию переменной силы.
 Механическим колебанием называется процесс, при котором характеристики движения принимают одни и те же значения через некоторые промежутки времени. Колебания, при которых значения физических величин, описывающих данный процесс, повторяются через равные промежутки времени называются периодическими. Минимальное значение этого промежутка времени называется периодом колебаний.
Виды колебаний Механическим колебанием называется процесс, при котором характеристики движения принимают одни и те же значения через некоторые промежутки времени. Колебания, при которых значения физических величин, описывающих данный процесс, повторяются через равные промежутки времени называются периодическими. Минимальное значение этого промежутка времени называется периодом колебаний.
Виды колебаний
 Колебания, возникающие в системе, не подвергающейся переменным внешним воздействиям после первоначального толчка, называются свободными. Примером свободных колебаний являются колебания математического маятника.
Колебания, возникающие в системе, не подвергающейся переменным внешним воздействиям после первоначального толчка, называются свободными. Примером свободных колебаний являются колебания математического маятника.
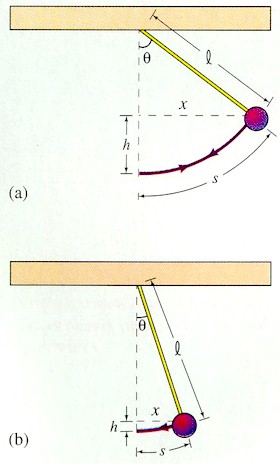 Если в процессе движения маятник не испытывает сил трения и сопротивления, то его малые колебания (угол отклонения от положения равновесия q < 6 градусов) можно считать гармоническими (см. тему 2).
При наличии в системе сил трения или сопротивления свободные колебания будут затухающими. Если в процессе движения маятник не испытывает сил трения и сопротивления, то его малые колебания (угол отклонения от положения равновесия q < 6 градусов) можно считать гармоническими (см. тему 2).
При наличии в системе сил трения или сопротивления свободные колебания будут затухающими.
 Колебания, возникающие в системе под воздействием переменной внешней силы, называются вынужденными.
Колебания, возникающие в системе под воздействием переменной внешней силы, называются вынужденными.

|
Сейчас на сайте
- See more at: http://e-science.ru/node/4365#sthash.nfWA21GH.dpuf
Колебательные движения
Самый простой случай К. движений уже рассмотрен в статье Гармоническое движение. Такое движение обуславливается переменной силой, во всякий момент направленной противоположно отклонению колеблющейся точки u, пропорциональной величине отклонений. Перемещение колеблющейся точки, в самом простом случае, выражается уравнением: x = αsin2π t / T, где α размах или амплитуда колебания, T — период одного колебания, t время, считаемое от момента прохождения точки чрез среднее свое положение и угол 2π t / T — фаза колебания. Фаза определяет место точки в пути и считается от 0 до 2π. Кинетическая энергия колеблющейся частицы (масса m), выражаемая, обыкновенно, через 1/2 mv 2 (живая сила), меняется в течение 1/2 периода от нуля до некоторого максимума. Поэтому средняя величина энергии для времени 1/2 периода выражается через π2 ma 2/ T 2. Все возможные типы колебаний могут быть приведены к простому колебанию — гармоническому. Фурье доказал особой теоремой, что всякое периодическое или К. движение с периодом T можно составить через сложение простых — с периодом T, 1/2 T, 1/3 T, и т.д. и притом составить только одним способом (т. е. с вполне определенными амплитудами и фазами). Иначе говоря, всякое К. движение с периодом Т разлагается на простые гармонические, причем период основного есть Т. Два простых колебания одного периода, следующие по одной и той же прямой, складываются — усиливая или ослабляя друг друга и даже уничтожая (если амплитуды равны, а фазы противоположны, т. е. разнятся на π). Такое явление называется интерференцией колебаний (см. Интерференция). Два колебания одинакового периода, направленные по взаимно перпендикулярным прямым, смотря по амплитудам и разности фаз, складываются или в движение по эллипсу (эллиптическое колебание), или по кругу (круговое колебание), или по прямой. Два колебания различных периодов по взаимно перпендикулярным линиям, в зависимости от амплитуд и разности фаз, складываются в траектории сложных форм, известных под общим именем фигур Лиссажу. Ряд точек, последовательно приходящих в К. движение, называется лучом. Передача колебаний от точки к точке — совершается с определенной скоростью, которая поэтому называется скоростью распространения колебаний. Расстояние между двумя ближайшими точками луча, находящимися в одинаковых фазах колебания, называется длиной волны (λ). Если в ряде точек в некоторый момент (t) перемещение одной точки ряда: x = а sin2π t / T, то перемещение всякой другой, находящейся в ряде на расстоянии y от первой, выразится уравнением x = a sin2π(t / Т-у /λ). Такое уравнение называется уравнением луча и y называется разностью хода двух колеблющихся точек. Она соответствует разности фаз 2π y /λ (см. Волны, Дифракция, Интерференция).
|
|
|
Подробнее о К. движении см. Thomson u. Tait, "Theoretische Physik übersetzt v. Helmholtz und Wertheim" (p. 57); Хвольсон, "Учение о движении и силах (1893, стр. 58); Столетов, "Введение в акустику и оптику" (M., 1895). См. еще Колебания звучащих тел.
Н. Егоров.
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
§1 Кинематика гармонического колебания
Процессы, повторяющиеся во времени называются колебаниями.
 В зависимости от природы колебательного процесса и механизма возбуждения бывают: механические колебания (колебания маятников, струн, зданий, земной поверхности и т.д.); электромагнитные колебания (колебания переменного тока, колебания векторов В зависимости от природы колебательного процесса и механизма возбуждения бывают: механические колебания (колебания маятников, струн, зданий, земной поверхности и т.д.); электромагнитные колебания (колебания переменного тока, колебания векторов  и и  в электромагнитной волне и т.д.); электромеханические колебания (колебания мембраны телефона, диффузора громкоговорителя и др.); колебания ядер и молекул в результате теплового движения в атомах.
Рассмотрим отрезок [ОД] (радиус-вектор), совершающий вращательное движение вокруг точки 0. Длина |ОД| = A. Вращение происходит с постоянной угловой скоростью ω0. Тогда угол φ между радиус-вектором и осью x меняется со временем по закону в электромагнитной волне и т.д.); электромеханические колебания (колебания мембраны телефона, диффузора громкоговорителя и др.); колебания ядер и молекул в результате теплового движения в атомах.
Рассмотрим отрезок [ОД] (радиус-вектор), совершающий вращательное движение вокруг точки 0. Длина |ОД| = A. Вращение происходит с постоянной угловой скоростью ω0. Тогда угол φ между радиус-вектором и осью x меняется со временем по закону
 где φ0 - угол между [ОД] и осью х в момент времени t = 0. Проекция отрезка [ОД] на ось х в момент времени t = 0
где φ0 - угол между [ОД] и осью х в момент времени t = 0. Проекция отрезка [ОД] на ось х в момент времени t = 0
 а в произвольный момент времени
а в произвольный момент времени
 (1)
Таким образом, проекция отрезка [ОД] на ось х совершает колебания, происходящие вдоль оси х, и эти колебания описываются законом косинуса (формула (1)).
Колебания, которые описываются законом косинуса (1)
Таким образом, проекция отрезка [ОД] на ось х совершает колебания, происходящие вдоль оси х, и эти колебания описываются законом косинуса (формула (1)).
Колебания, которые описываются законом косинуса
 или синуса
или синуса
 называется гармоническими.
Гармонические колебания являются периодическими, т.к. значение величины х (и у) повторяется через равные промежутки времени.
Если отрезок [ОД] находится з низшем положении по рисунку, т.е. точка Д совпадает с точкой Р, то его проекция на ось х равна нулю. Назовем такое положение отрезка [ОД] положением равновесия. Тогда можно сказать, что величина х описывает смещение колеблющейся точки из положения равновесия. Максимальное смещение от положения равновесия называется амплитудой колебания
называется гармоническими.
Гармонические колебания являются периодическими, т.к. значение величины х (и у) повторяется через равные промежутки времени.
Если отрезок [ОД] находится з низшем положении по рисунку, т.е. точка Д совпадает с точкой Р, то его проекция на ось х равна нулю. Назовем такое положение отрезка [ОД] положением равновесия. Тогда можно сказать, что величина х описывает смещение колеблющейся точки из положения равновесия. Максимальное смещение от положения равновесия называется амплитудой колебания
 Величина
Величина
 которая стоит под знаком косинуса называется фазой. Фаза определяет смещение от положения равновесия в произвольный момент времени t. Фаза в начальный момент времени t = 0, равная φ0 называется начальной фазой.
которая стоит под знаком косинуса называется фазой. Фаза определяет смещение от положения равновесия в произвольный момент времени t. Фаза в начальный момент времени t = 0, равная φ0 называется начальной фазой.
 Промежуток времени, за который совершается одно полное колебание, называется периодом колебаний Т. Число колебаний в единицу времени называется частотой колебаний ν.
Промежуток времени, за который совершается одно полное колебание, называется периодом колебаний Т. Число колебаний в единицу времени называется частотой колебаний ν. Промежуток времени, за который совершается одно полное колебание, называется периодом колебаний Т. Число колебаний в единицу времени называется частотой колебаний ν.
Промежуток времени, за который совершается одно полное колебание, называется периодом колебаний Т. Число колебаний в единицу времени называется частотой колебаний ν.
 Через промежуток времени, равный периоду Т, т.е. при увеличении аргумента косинуса на ω0 Т, движение повторяется, и косинус принимает прежнее значение
Через промежуток времени, равный периоду Т, т.е. при увеличении аргумента косинуса на ω0 Т, движение повторяется, и косинус принимает прежнее значение
 т.к. период косинуса равен 2π, то, следовательно, ω0 Т = 2π
т.к. период косинуса равен 2π, то, следовательно, ω0 Т = 2π

 таким образом, ω0 - это число колебаний тела за 2π секунд. ω0 - циклическая или круговая частота.
рисунок гармонического колебания
А - амплитуда, Т – период, х - смещение, t – время.
Скорость колеблющейся точки найдем, продифференцировав уравнение смещения х (t) по времени таким образом, ω0 - это число колебаний тела за 2π секунд. ω0 - циклическая или круговая частота.
рисунок гармонического колебания
А - амплитуда, Т – период, х - смещение, t – время.
Скорость колеблющейся точки найдем, продифференцировав уравнение смещения х (t) по времени

 т.е. скорость v отличается по фазе от смещения х на π/2.
Ускорение - первая производная от скорости (вторая производная от смещения) по времени
т.е. скорость v отличается по фазе от смещения х на π/2.
Ускорение - первая производная от скорости (вторая производная от смещения) по времени 
 т.е. ускорение а отличается от смещения по фазе на π.
т.е. ускорение а отличается от смещения по фазе на π.
 Построим график х(t), у(t) и а(t) в одной смете координат (для простоты примем φ0= 0 и ω0 = 1)
Свободными или собственными называются колебания, которые происходят в системе предоставленной самой себе после того, как она была выведена из положения равновесия. Построим график х(t), у(t) и а(t) в одной смете координат (для простоты примем φ0= 0 и ω0 = 1)
Свободными или собственными называются колебания, которые происходят в системе предоставленной самой себе после того, как она была выведена из положения равновесия.
| ||
Механические колебания Основные формулы Всякое колебательное движение, в том числе и гармоническое, характеризуется амплитудой 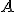 , периодом колебаний , периодом колебаний 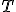 , частотой , частотой 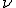 , циклической (круговой) частотой , циклической (круговой) частотой 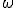 и фазой колебаний и фазой колебаний 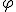 . Амплитудой . Амплитудой 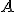 называют наибольшее значение колеблющейся величины (максимальное смещение от положения равновесия). Число полных колебаний в единицу времени называют частотой: называют наибольшее значение колеблющейся величины (максимальное смещение от положения равновесия). Число полных колебаний в единицу времени называют частотой: 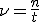 . Циклическая (круговая) частота - это число полных колебаний в течении . Циклическая (круговая) частота - это число полных колебаний в течении 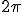 с: с: 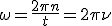 . Периодом называю время, в течении которого совершается одно полное колебание: . Периодом называю время, в течении которого совершается одно полное колебание: 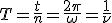 . Смещение, скорость и ускорение при гармоническом колебании определяются уравнениями . Смещение, скорость и ускорение при гармоническом колебании определяются уравнениями 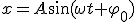 , , 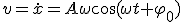 , , 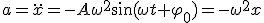 . Здесь . Здесь 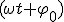 - фаза колебаний, а - фаза колебаний, а 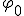 - начальная фаза. Сила, действующая на тело при свободном гармоническом колебании (квазиупругая сила), всегда пропорциональна смещению и направлена в сторону, противоположную смещению: - начальная фаза. Сила, действующая на тело при свободном гармоническом колебании (квазиупругая сила), всегда пропорциональна смещению и направлена в сторону, противоположную смещению: 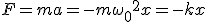 где где 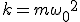 - коэффициент квазиупругой силы, измеряемый силой, вызывающей смещение - коэффициент квазиупругой силы, измеряемый силой, вызывающей смещение 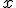 , равное единице. При отсутствии сопротивления среды циклическая частота , равное единице. При отсутствии сопротивления среды циклическая частота 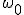 свободных гармонических колебаний, называемых собственной циклической частотой и период свободных гармонических колебаний, называемых собственной циклической частотой и период 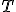 равны: равны: 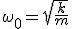 , ,  Период колебания математического маятника длиной Период колебания математического маятника длиной 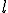 равен равен 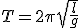 . Период колебаний физического маятника . Период колебаний физического маятника 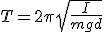 , где , где 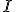 - момент инерции маятника относительно оси качаний, - момент инерции маятника относительно оси качаний, 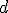 - расстояние от оси его до центра тяжести. Полная энергия тела, совершающего гармонические колебания, постоянна и равна - расстояние от оси его до центра тяжести. Полная энергия тела, совершающего гармонические колебания, постоянна и равна 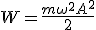 . Уравнение смещения в затухающих колебаниях при наличии силы сопротивления . Уравнение смещения в затухающих колебаниях при наличии силы сопротивления 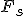 пропорциональной скорости ( пропорциональной скорости (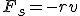 , где , где  - коэффициент сопротивления) имеет вид: - коэффициент сопротивления) имеет вид: 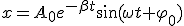 . Здесь . Здесь 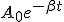 - убывающая по времени амплитуда смещения; - убывающая по времени амплитуда смещения; 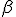 - коэффициент затухания; - коэффициент затухания; 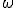 - циклическая частота; - циклическая частота; 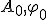 - начальные амплитуда и фаза, определяются из начальных условий. Величины - начальные амплитуда и фаза, определяются из начальных условий. Величины 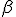 и и 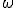 выражаются через параметры системы выражаются через параметры системы 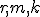 формулами: формулами: 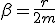 , , 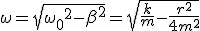 . Логарифмический декремент затухания . Логарифмический декремент затухания 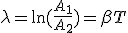 , где , где 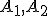 - амплитуды двух последовательных колебаний. Амплитуда вынужденных колебаний - амплитуды двух последовательных колебаний. Амплитуда вынужденных колебаний 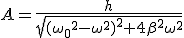 , где , где 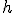 - есть отношение амплитуды вынуждающей силы к массе тела; - есть отношение амплитуды вынуждающей силы к массе тела; 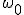 - собственная циклическая частота; - собственная циклическая частота; 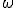 - циклическая частота вынуждающей силы. Резонансная циклическая частота равна - циклическая частота вынуждающей силы. Резонансная циклическая частота равна 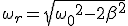 . Динамика колебательного движения Задача 1. Шарик массой 20 г колеблется с периодом 2 с. В начальный момент времени шарик обладал энергией 0,01 Дж и находился от положения равновесия на расстоянии 2,5 см. Составить уравнение гармонического колебания и закон изменения возвращающей силы с течением времени. Решение. Запишем краткое условие задачи. Найти: . Динамика колебательного движения Задача 1. Шарик массой 20 г колеблется с периодом 2 с. В начальный момент времени шарик обладал энергией 0,01 Дж и находился от положения равновесия на расстоянии 2,5 см. Составить уравнение гармонического колебания и закон изменения возвращающей силы с течением времени. Решение. Запишем краткое условие задачи. Найти: 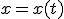 , , 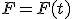 Дано: Дано: 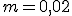 кг, кг, 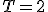 с, с, 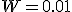 Дж, Дж, 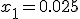 м. Выберем в качестве ИСО "Лабораторию" - помещение в котором мы наблюдаем колебание шарика. Задачи часто решают в лабораторной ИСО. Будем искать м. Выберем в качестве ИСО "Лабораторию" - помещение в котором мы наблюдаем колебание шарика. Задачи часто решают в лабораторной ИСО. Будем искать 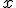 в виде в виде 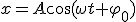 . (1) Так как период колебаний известен, то . (1) Так как период колебаний известен, то  c-1. Амплитуду колебаний найдем из выражения для энергии c-1. Амплитуду колебаний найдем из выражения для энергии 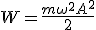 , откуда , откуда 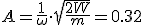 м. Воспользуемся теперь условием начального момента м. Воспользуемся теперь условием начального момента 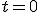 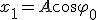 . . 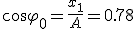 , откуда , откуда 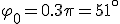 Подставляя найденные значения в (1), получим: Подставляя найденные значения в (1), получим: 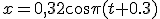 . Если на тело массы . Если на тело массы 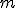 действует квазиупругая сила, то тело совершает гармонические колебания с циклической частотой действует квазиупругая сила, то тело совершает гармонические колебания с циклической частотой 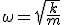 , откуда , откуда 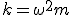 Тогда Тогда 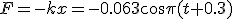 . Задача 2. Тело, неподвижно висящее на цилиндрической пружине, растягивает её на . Задача 2. Тело, неподвижно висящее на цилиндрической пружине, растягивает её на 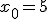 см. Затем тело было смещено из положения равновесия по вертикали и отпущено, в результате чего оно стало совершать колебания. Найти их период. Решение. Запишем краткое условие задачи. Найти: см. Затем тело было смещено из положения равновесия по вертикали и отпущено, в результате чего оно стало совершать колебания. Найти их период. Решение. Запишем краткое условие задачи. Найти: 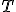 Дано: Дано: 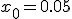 м. Выберем в качестве ИСО точку подвеса пружины, ось OX направим вертикально вниз. На тело действуют две силы: сила тяжести м. Выберем в качестве ИСО точку подвеса пружины, ось OX направим вертикально вниз. На тело действуют две силы: сила тяжести 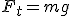 и сила упругости пружины и сила упругости пружины 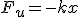 . Когда тело покоится, равнодействующая приложенных к нему сил равна нулю: . Когда тело покоится, равнодействующая приложенных к нему сил равна нулю: 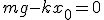 . Отсюда можем сразу найти коэффициент жесткости пружины: . Отсюда можем сразу найти коэффициент жесткости пружины: 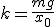 . Пусть теперь тело смещено от положения равновесия на . Пусть теперь тело смещено от положения равновесия на 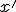 и пружина растянулась на величину и пружина растянулась на величину 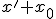 . Равнодействующая сил в этом случае есть . Равнодействующая сил в этом случае есть 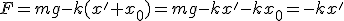 . Мы видим, что и при наличии силы тяжести тело будет совершать гармонические колебания, период которых можно определить по формуле . Мы видим, что и при наличии силы тяжести тело будет совершать гармонические колебания, период которых можно определить по формуле 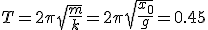 c. Задача 3. Ареометр массы c. Задача 3. Ареометр массы 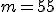 г, плавающий в растворе серной кислоты, указывает, что плотность жидкости г, плавающий в растворе серной кислоты, указывает, что плотность жидкости 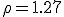 г/см3. Если прибор сместить из положения его равновесия немного по вертикали и отпустить, он начнет колебаться. Считая колебания незатухающими, определить их период, если радиус цилиндрической трубки ареометра, в которой заключена его шкала, равен г/см3. Если прибор сместить из положения его равновесия немного по вертикали и отпустить, он начнет колебаться. Считая колебания незатухающими, определить их период, если радиус цилиндрической трубки ареометра, в которой заключена его шкала, равен 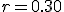 см. Решение. Запишем краткое условие задачи. Найти: см. Решение. Запишем краткое условие задачи. Найти: 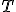 Дано: Дано: 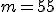 г. г. 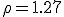 г/см3. г/см3. 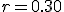 см. По правила надо было бы перевести данные величины в СИ, но поскольку мы ищем период, который измеряется в секундах, мы этого делать не будем, хотя это и не очень правильно. Выберем в качестве ИСО сосуд с кислотой, т.е. в нашей задаче сосуд и кислота неподвижны. Ось см. По правила надо было бы перевести данные величины в СИ, но поскольку мы ищем период, который измеряется в секундах, мы этого делать не будем, хотя это и не очень правильно. Выберем в качестве ИСО сосуд с кислотой, т.е. в нашей задаче сосуд и кислота неподвижны. Ось 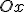 направим вниз. На погруженный в жидкость ареометр действуют две силы: сила тяжести направим вниз. На погруженный в жидкость ареометр действуют две силы: сила тяжести 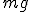 и выталкивающая, архимедова, сила и выталкивающая, архимедова, сила 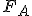 , равная весу жидкости, вытесненной телом: , равная весу жидкости, вытесненной телом: 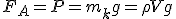 , (1) где , (1) где 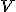 - объем вытесненной жидкости, равный объему погруженной в кислоту части ареометра. Если ареометр находится в равновесии, то приложенные к нему силы уравновешены. - объем вытесненной жидкости, равный объему погруженной в кислоту части ареометра. Если ареометр находится в равновесии, то приложенные к нему силы уравновешены. 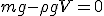 . Сместим ареометр из положения равновесия на величину . Сместим ареометр из положения равновесия на величину 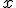 вниз. В силу изменения объема погруженной в жидкость нижней части ареометра изменится и архимедова сила. На ареометр будет действовать равнодействующая сила, направленная вниз: вниз. В силу изменения объема погруженной в жидкость нижней части ареометра изменится и архимедова сила. На ареометр будет действовать равнодействующая сила, направленная вниз: 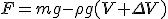 . (2) Здесь . (2) Здесь 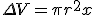 - изменение объема погруженной части прибора. Подставляя в (2) это значение и учитывая (1), получим: - изменение объема погруженной части прибора. Подставляя в (2) это значение и учитывая (1), получим: 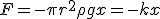 , где , где 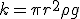 - постоянная величина. мы видим, что на ареометр действует сила, пропорциональная смещению, взятому с обратным знаком, т.е. квазиупругая сила. Следовательно, он совершает гармонические колебания, период которых может быть найден по формуле - постоянная величина. мы видим, что на ареометр действует сила, пропорциональная смещению, взятому с обратным знаком, т.е. квазиупругая сила. Следовательно, он совершает гармонические колебания, период которых может быть найден по формуле  или или 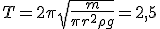 с.
Сообщение было отредактировано iskander (2012-08-21 12:07 GMT, назад)
Механические колебания
11 класс
• Механические колебания – это движения, которые точно или приблизительно повторяются через определенные интервалы времени
•По характеру физических процессов в системе, которые вызывают колебательные движения, различают три основных вида колебаний:
•Вынужденные колебания – это колебания, которые происходят под действием внешней, периодически изменяющейся силы.
•Свободные колебания – это колебания, которые возникли в системе под действием внутренних сил, после того, как система была выведена из положения устойчивого равновесия.
•Автоколебаниями называются незатухающие колебания, которые могут существовать в системе без воздействия на неё внешних периодических сил.
Колебательные системы
Колебательные системы
Условия возникновения колебаний
•Наличие положения устойчивого равновесия, при котором равнодействующая сила равна нулю.
•Хотя бы одна сила должна зависеть от координат.
•Наличие в колеблющейся материальной точке избыточной энергии.
•Если вывести тело из положения равновесия, то равнодействующая не равна нулю.
•Силы трения в системе малы.
Превращение энергии при колебательном движении
•В неустойчивом равновесии имеем
Еп –- Ек-- Еп-- Ек -- Еп
•За полное колебание (колебательное движение, которое вновь повторяется, называют полным колебанием)
•Выполняется закон сохранения энергии.
Параметры колебательного движения
• Смещение х –отклонение колеблющейся точки от положения равновесия в данный момент времени.
• Амплитуда хmax или А – наибольшее смещение от положения равновесия.
• Период Т – время одного полного колебания. Выражается в секундах.
• Частота - число полных колебаний за единицу времени. Выражается в герцах(Гц).
•Циклическая (круговая) частота колебаний – частота, равная числу колебаний, совершаемых материальной точкой за
Свободные колебания пружинного маятника
•Fx=-kx – закон Гука
•Fx=max – второй закон Ньютона
•max=-kx, ax= - kx/m, k/m=const
уравнение свободных колебаний
пружинного маятника.
•Ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело, но пропорционально смещению и направлено в сторону равновесия.
Домашнее задание
•Г.Я. Мякишев, А.З. Синяков
Физика 11 класс
Колебания и волны
Параграфы 1.1 – 1.2
“Какой общий признак у всех колебательных процессов?”
(привожу в колебание все колебательные системы).
Ученик: - периодичность, повторяемость.
- колебания – это движения или процессы, которые точно или приблизительно повторяются через определенные промежутки времени. (Приложение №1)
2. Учитель: При изучении теории колебаний используют простейшие колебательные системы, маятники, которые представлены в виде демонстраций.
Колебательная система – это система тел, способных совершать колебательные движения. (Приложение №1, рис.3)
Маятник – это твердое тело, подвешенное на нити или на пружине и совершающее колебания под действием силы тяжести. (Приложение №1)
Существуют два вида маятников:
Математический маятник – это материальная точка, подвешенная на невесомой и нерастяжимой нити, находящаяся в поле тяжести Земли. (Приложения №1, №3 (слайд 1), рис.1)
mнити <<mгр,lнити>> чгр
Пружинный маятник – тело, подвешенное на пружине и совершающее колебания вдоль вертикальной оси под действием силы упругости пружины.[1] (Приложения №1, №3 (слайд 3) рис.2)
Маятники – это колебательные системы. (Приложение №1).
3. Учитель: Каждая из колебательных систем приводится в колебательное движение, причем один из маятников приподнимается над его начальным положением, другой толчком приводится в колебание, колебание пружинного маятника достигается отклонением тела от начального положения. Но результат колебаний для всех колебательных систем будет одинаков. Маятники начнут колебаться. Почему?
Ученик: Все колебательные системы отклонили от положения равновесия.
Учитель: Основное свойство колебательных систем – наличие положения устойчивого равновесия (п.р.). (Приложения №1, №2)
В положении равновесия равнодействующая силы тяжести и силы упругости равна нулю. Центр тяжести должен быть ниже точки подвеса. [1]
4. Учитель: Колебания по способу возбуждения и характеру физических процессов делятся на 4 вида. Мы познакомимся с двумя из них – свободными и вынужденными. Изучение колебаний мы начнем с рассмотрения свободных колебаний.
Свободные колебания– это колебания под действием внутренних сил системы благодаря начальному запасу энергии[2]. По ОК и по рисунку определяем, какие силы являются внутренними для математического и для пружинного маятника. (Приложение №2)
Ученик: Для математического маятника внутренними силами являются силы тяжести и натяжение нити, а для пружинного – силы тяжести и упругости пружины.
Учитель: Приведем маятник в колебательное движение, т.е. отклоним маятник от положения равновесия, по-другому говорят – совершим работу против силы тяжести.
Будет ли равнодействующая сил по-прежнему равна нулю?
Ученик: Теперь FR с.
Сообщение было отредактировано iskander (2012-08-21 12:07 GMT, назад)
Механические колебания
11 класс
• Механические колебания – это движения, которые точно или приблизительно повторяются через определенные интервалы времени
•По характеру физических процессов в системе, которые вызывают колебательные движения, различают три основных вида колебаний:
•Вынужденные колебания – это колебания, которые происходят под действием внешней, периодически изменяющейся силы.
•Свободные колебания – это колебания, которые возникли в системе под действием внутренних сил, после того, как система была выведена из положения устойчивого равновесия.
•Автоколебаниями называются незатухающие колебания, которые могут существовать в системе без воздействия на неё внешних периодических сил.
Колебательные системы
Колебательные системы
Условия возникновения колебаний
•Наличие положения устойчивого равновесия, при котором равнодействующая сила равна нулю.
•Хотя бы одна сила должна зависеть от координат.
•Наличие в колеблющейся материальной точке избыточной энергии.
•Если вывести тело из положения равновесия, то равнодействующая не равна нулю.
•Силы трения в системе малы.
Превращение энергии при колебательном движении
•В неустойчивом равновесии имеем
Еп –- Ек-- Еп-- Ек -- Еп
•За полное колебание (колебательное движение, которое вновь повторяется, называют полным колебанием)
•Выполняется закон сохранения энергии.
Параметры колебательного движения
• Смещение х –отклонение колеблющейся точки от положения равновесия в данный момент времени.
• Амплитуда хmax или А – наибольшее смещение от положения равновесия.
• Период Т – время одного полного колебания. Выражается в секундах.
• Частота - число полных колебаний за единицу времени. Выражается в герцах(Гц).
•Циклическая (круговая) частота колебаний – частота, равная числу колебаний, совершаемых материальной точкой за
Свободные колебания пружинного маятника
•Fx=-kx – закон Гука
•Fx=max – второй закон Ньютона
•max=-kx, ax= - kx/m, k/m=const
уравнение свободных колебаний
пружинного маятника.
•Ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело, но пропорционально смещению и направлено в сторону равновесия.
Домашнее задание
•Г.Я. Мякишев, А.З. Синяков
Физика 11 класс
Колебания и волны
Параграфы 1.1 – 1.2
“Какой общий признак у всех колебательных процессов?”
(привожу в колебание все колебательные системы).
Ученик: - периодичность, повторяемость.
- колебания – это движения или процессы, которые точно или приблизительно повторяются через определенные промежутки времени. (Приложение №1)
2. Учитель: При изучении теории колебаний используют простейшие колебательные системы, маятники, которые представлены в виде демонстраций.
Колебательная система – это система тел, способных совершать колебательные движения. (Приложение №1, рис.3)
Маятник – это твердое тело, подвешенное на нити или на пружине и совершающее колебания под действием силы тяжести. (Приложение №1)
Существуют два вида маятников:
Математический маятник – это материальная точка, подвешенная на невесомой и нерастяжимой нити, находящаяся в поле тяжести Земли. (Приложения №1, №3 (слайд 1), рис.1)
mнити <<mгр,lнити>> чгр
Пружинный маятник – тело, подвешенное на пружине и совершающее колебания вдоль вертикальной оси под действием силы упругости пружины.[1] (Приложения №1, №3 (слайд 3) рис.2)
Маятники – это колебательные системы. (Приложение №1).
3. Учитель: Каждая из колебательных систем приводится в колебательное движение, причем один из маятников приподнимается над его начальным положением, другой толчком приводится в колебание, колебание пружинного маятника достигается отклонением тела от начального положения. Но результат колебаний для всех колебательных систем будет одинаков. Маятники начнут колебаться. Почему?
Ученик: Все колебательные системы отклонили от положения равновесия.
Учитель: Основное свойство колебательных систем – наличие положения устойчивого равновесия (п.р.). (Приложения №1, №2)
В положении равновесия равнодействующая силы тяжести и силы упругости равна нулю. Центр тяжести должен быть ниже точки подвеса. [1]
4. Учитель: Колебания по способу возбуждения и характеру физических процессов делятся на 4 вида. Мы познакомимся с двумя из них – свободными и вынужденными. Изучение колебаний мы начнем с рассмотрения свободных колебаний.
Свободные колебания– это колебания под действием внутренних сил системы благодаря начальному запасу энергии[2]. По ОК и по рисунку определяем, какие силы являются внутренними для математического и для пружинного маятника. (Приложение №2)
Ученик: Для математического маятника внутренними силами являются силы тяжести и натяжение нити, а для пружинного – силы тяжести и упругости пружины.
Учитель: Приведем маятник в колебательное движение, т.е. отклоним маятник от положения равновесия, по-другому говорят – совершим работу против силы тяжести.
Будет ли равнодействующая сил по-прежнему равна нулю?
Ученик: Теперь FR  0, т.е. возникает равнодействующая сил, возвращающая маятник к положению равновесия. [1] (Приложения №2, №3 (слайд 6), рис.1, рис.4)
Учитель: Равнодействующая сил возникает при отклонении тела от положения равновесия.
Х м – смещение или отклонение тела от положения равновесия. (Приложение №2, рис.9)
Свободные колебания - … 0, т.е. возникает равнодействующая сил, возвращающая маятник к положению равновесия. [1] (Приложения №2, №3 (слайд 6), рис.1, рис.4)
Учитель: Равнодействующая сил возникает при отклонении тела от положения равновесия.
Х м – смещение или отклонение тела от положения равновесия. (Приложение №2, рис.9)
Свободные колебания - …
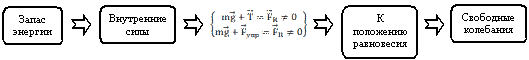 Мы можем привести в колебательное движение систему, задав начальные условия.
Причем можем задать начальные условия колебаний, т.е. начальные условия определяют максимальное отклонение маятника от положению равновесия т.е. амплитуду. [2] (Приложение №3 (слайд 6), рис10)
Мы можем привести в колебательное движение систему, задав начальные условия.
Причем можем задать начальные условия колебаний, т.е. начальные условия определяют максимальное отклонение маятника от положению равновесия т.е. амплитуду. [2] (Приложение №3 (слайд 6), рис10)
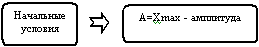 Амплитуда - максимальное отклонение тела от положения равновесия
Как долго маятник будет колебаться? Давайте проследим аналогично с качелями. Представим себе, как вы сели на качели, привели их в колебания, начали качаться.
- Как долго вы будете качаться?
Ученик: - Пока силы трения в системе не остановят качели.
Учитель: - Совершенно верно, то же будет и с маятником.
Чтобы колебания происходили долго, надо чтобы силы трения были малы, иначе колебания прекратятся. Говорят, что свободные колебания – это затухающие колебания.
ОК. Свободные колебания – затухающие колебания. (Приложение №2, рис.10) Одно из условий колебаний – отсутствие силы трения. Может ли быть абсолютное отсутствие силы трения?
Ученик: Нет, но силы трения дол
Амплитуда - максимальное отклонение тела от положения равновесия
Как долго маятник будет колебаться? Давайте проследим аналогично с качелями. Представим себе, как вы сели на качели, привели их в колебания, начали качаться.
- Как долго вы будете качаться?
Ученик: - Пока силы трения в системе не остановят качели.
Учитель: - Совершенно верно, то же будет и с маятником.
Чтобы колебания происходили долго, надо чтобы силы трения были малы, иначе колебания прекратятся. Говорят, что свободные колебания – это затухающие колебания.
ОК. Свободные колебания – затухающие колебания. (Приложение №2, рис.10) Одно из условий колебаний – отсутствие силы трения. Может ли быть абсолютное отсутствие силы трения?
Ученик: Нет, но силы трения дол
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

