Критерий равенства дисперсий ряда генеральных

Совокупностей

 

 

Нулевая гипотеза в этом случае заключается в том, что все m генеральных совокупностей, из которых взяты выборки, имеют равные дисперсии, т.е. σ²₁ = σ²₂ = … = σ²_m = σ².

Критерий Хартлея. Применяется при одинаковых объёмах выборки n ₁ = n ₂ = … n _m = n. Выдвигается нулевая гипотеза о равенстве (однородности) ряда дисперсий σ²₁ = σ²₂ = … = σ²_m = σ². Критерий предусматривает вычисление статистики

F _max = ≤ F _{max α}. (3.11)

При выполнении неравенства нулевую гипотезу не отвергают. В противном случае – отвергают и принимают альтернативную гипотезу.

Пример 3.5. Испытано на растяжение 5 серий по 20 образцов. Значения выборочных дисперсий составляют: s ²₁ = 154; s ²₂ = 208; s ²₃ = 186; s ²₄ = 197; s ²₄ = 153.

Требуется проверить гипотезу о равенстве генеральных дисперсий предела прочности материала при альтернативной гипотезе σ²₁ ≠ σ²₂.

По формуле (3.11)

F _max = = 1,36

По таблице 3.4 для α = 0,05; m = 5 и k = 20 – 1 = 19

F _{max 0.05} = 3,71

Условие (3.11) выполняется

Заключение: дисперсии равны друг другу.

Таблица 3.4 – Критические значения критерия Хартлея F _{max α}

k = n –1	m
	39,0	87,5					40,3
	15,4 47,5	27,8	39,2	50,7	62,0	72,9	83,5	93,9
	9,60 23,2	15,5 37,0	20,6	25,2	29,5	33,6	37,5	41,1	44,6	48,0	51,4
	7,15 14,9	10,8	13,7	16,3	18,7	20,8	22,9	24,7	26,5	28,2	29,9
	5,82 11,1	8,38 15,5	10,4 19,1	21,1	13,7	15,0	16,3	17,5	18,6	19,7	20,7
	4,99 8,89	6,94 12,1	8,44 14,5	9,70 16,5	10,8 18,4	11,8	12,7	13,5	14,3	15,1	15,8
	4,43 7,50	6,00 9,9	7,18 11,7	8,12 13,2	9,03 14,5	9,78 15,8	10,5 16,9	11,1 17,9	11,7 18,9	12,2 19,8	12,7
	4,03 6,54	5,34 8,5	6,31 9,9	7,11 11,1	7,80 12,1	8,41 3,1	8,95 13,9	9,45 14,7	9,91 15,3	10,3 16,0	10,7 16,6
	3,72 5,85	4,85 7,4	5,67 8,6	6,34 9,6	6,92 10,4	7,42 11,1	7,87 11,8	8,28 12,4	8,66 12,9	9,01 13,4	9,34 13,9
	3,28 4,91	4,16 6,1	4,79 6,9	5,30 7,6	5,72 8,2	6,09 8,7	6,42 9,1	6,72 9,5	7,00 9,9	7,25 10,2	7,48 10,6
	2,86 4,07	3,54 4,9	4,01 5,5	4,37 6,0	4,68 6,4	4,95 6,7	5,19 7,1	5,40 7,3	5,59 7,5	5,77 7,8	5,93 8,0
	2,46 3,32	2,95 3,8	3,29 4,3	3,54 4,6	3,76 4,9	3,94 5,1	4,10 5,3	4,24 5,5	4,37 5,6	4,49 5,8	4,59 5,9
	2,07 2,63	2,40 3,0	2,61 3,3	2,78 3,4	2,91 3,6	3,02 3,7	3,12 3,8	3,21 3,9	3,29 4,0	3,36 4,1	3,39 4,2
	1,67 1,96	1,85 2,2	1,96 2,3	2,04 2,4	2,11 2,4	2,17 2,5	2,22 2,5	2,26 2,6	2,30 2,6	2,33 2,7	2,36 2,7
Примечание. Верхняя строка в каждой графе для α = 0,05; нижняя – для α = 0,01

 

Критерий Кочрена. Используется также при равных объёмах отдельных выборок и является предпочтительным по сравнению с критерием Хартлея в случаях, когда одна из выборочных дисперсий значительно больше остальных, а также при m > 12.

Находят статистику

G _max = ≤ G _α. (3.12)

При выполнении неравенства нулевую гипотезу не отвергают. В противном случае – отвергают и принимают альтернативную гипотезу.

Пример 3.6. Проверить нулевую гипотезу Н ₀: σ²₁ = σ²₂ = … = σ² по условию примера 3.5

По формуле (3.12)

G _max = = 0,232

По таблице 3.5 для α = 0,05; m = 5 и k = 20 – 1 = 19

G _α = G _0,05 = 0,356

Условие (3.12) выполняется

Заключение: гипотеза принимается.

Таблица 3.5 – Критические значения критерия Кочрена G _α

m	k = n – 1
													∞
	0,9958 0,9990	0,9750 0,9950	0,9392 0,9794	0,9057 0,9586	0,8772 0,9373	0,8534 0,9172	0,5332 0,8988	0,8159 0,8823	0,8010 0,8674	0,7880 0,8539	0,7341 0,7949	0,6602 0,7067	0,5813 0,6062	0,5000 0,5000
	0,9669 0,9933	0,8709 0,9423	0,7977 0,8831	0,7457 0,8335	0,7071 0,7933	0,6771 0,7606	0,6530 0,7335	0,6333 0,7107	0,6167 0,6912	0,6025 0,6743	0,5466 0,6059	0,4748 0,5153	0,4031 0,4230	0,3333 0,3333
	0,9065 0,9676	0,7679 0,8643	0,6841 0,7814	0,6287 0,7212	0,5895 0,6761	0,5598 0,6410	0,5365 0,6129	0,5175 0,5897	0,5017 0,5702	0,4884 0,5536	0,4366 0,4884	0,3720 0,4057	0,3093 0,3251	0,2500 0,2500
	0,8412 0,9279	0,6838 0,7885	0,5981 0,6957	0,5441 0,6329	0,5065 0,5875	0,4783 0,5531	0,4564 0,5259	0,4387 0,5037	0,4241 0,4854	0,4118 0,4697	0,3645 0,4094	0,3066 0,3351	0,2513 0,2644	0,2000 0,2000
	0,7808 0,8828	0,6161 0,7218	0,5321 0,6258	0,4803 0,5635	0,4447 0,5195	0,4184 0,4866	0,3980 0,4608	0,3817 0,4401	0,3682 0,4229	0,3568 0,4084	0,3135 0,3529	0,2612 0,2858	0,2119 0,2229	0,1667 0,1667
	0,7271 0,8376	0,5612 0,6644	0,4800 0,5685	0,4307 0,5080	0,3974 0,4695	0,3726 0,4347	0,3535 0,4105	0,3384 0,3911	0,3259 0,3751	0,3154 0,3616	0,2756 0,3105	0,2278 0,2494	0,1833 0,1929	0,1429 0,1429
	0,6798 0,7945	0,5157 0,6152	0,4377 0,5209	0,3910 0,4627	0,3595 0,4226	0,3362 0,3932	0,3185 0,3704	0,3043 0,3522	0,2926 0,3373	0,2829 0,3248	0,2462 0,2779	0,2022 0,2214	0,1616 0,1700	0,1250 0,1250
	0,6385 0,7544	0,4775 0,5727	0,4027 0,4810	0,3584 0,4251	0,3286 0,3870	0,3067 0,3592	0,2901 0,3378	0,2768 0,3207	0,2659 0,3067	0,2568 0,2950	0,2226 0,2514	0,1820 0,1992	0,1446 0,1521	0,1111 0,1111
	0,6020 0,7175	0,4450 0,5358	0,3733 0,4469	0,3311 0,3934	0,3029 0,3572	0,2823 0,3308	0,2666 0,3106	0,2541 0,2945	0,2439 0,2813	0,2353 0,2704	0,2032 0,2297	0,1655 0,1811	0,1308 0,1376	0,1000 0,1000
	0,5410 0,6528	0,3924 0,4751	0,3264 0,3919	0,2880 0,3328	0,2624 0,3099	0,2439 0,2861	0,2299 0,2680	0,2187 0,2535	0,2098 0,2419	0,2020 0,2320	0,1737 0,1961	0,1403 0,1535	0,1100 0,1157	0,0833 0,0833
	0,4709 0,5747	0,3346 0,4069	0,2758 0,3317	0,2419 0,2882	0,2195 0,2593	0,2034 0,2386	0,1911 0,2228	0,1815 0,2104	0,1736 0,2002	0,1671 0,1918	0,1429 0,1612	0,1144 0,1251	0,0889 0,0934	0,0667 0,0667
	0,3894 0,4799	0,2705 0,3297	0,2205 0,2654	0,1921 0,2288	0,1735 0,2048	0,1602 0,1877	0,1501 0,1748	0,1422 0,1646	0,1357 0,1567	0,1303 0,1501	0,1108 0,1248	0,0879 0,0960	0,0675 0,0709	0,0500 0,0500
	0,3434 0,4247	0,2354 0,2871	0,1907 0,2295	0,1656 0,1970	0,1493 0,1759	0,1374 0,1608	0,1286 0,1495	0,1216 0,1406	0,1160 0,1338	0,1113 0,1283	0,0942 0,1060	0,0743 0,0810	0,0567 0,0595	0,0417 0,0417
	0,2929 0,3632	0,1980 0,2412	0,1593 0,1913	0,1377 0,1635	0,1237 0,1454	0,1137 0,1327	0,1061 0,1232	0,1002 0,1157	0,0958 0,1100	0,0921 0,1054	0,0771 0,0867	0,0604 0,0658	0,0457 0,0480	0,0333 0,0333
	0,2370 0,2940	0,1576 0,1915	0,1259 0,1508	0,1082 0,1281	0,0968 0,1135	0,0887 0,1033	0,0827 0,0957	0,0780 0,0898	0,0745 0,0853	0,0713 0,0816	0,0595 0,0668	0,0462 0,0503	0,0347 0,0363	0,0250 0,0250
	0,1737 0,2151	0,1131 0,1371	0,0895 0,1069	0,0765 0,0902	0,0682 0,0796	0,0623 0,0722	0,0583 0,0668	0,0552 0,0625	0,0520 0,0594	0,0497 0,0567	0,0411 0,0461	0,0316 0,0344	0,0234 0,0245	0,0167 0,0167
	0,0998 0,1225	0,0632 0,0759	0,0495 0,0585	0,0419 0,0489	0,0371 0,0429	0,0337 0,0387	0,0312 0,0357	0,0292 0,0334	0,0279 0,0316	0,0266 0,0302	0,0218 0,0242	0,0165 0,0178	0,0120 0,0125	0,0083 0,0083
Примечание. Верхняя строка в каждой графе для α = 0,05; нижняя – для α = 0,01

Критерий Бартлета. При неодинаковом числе образцов в отдельных партиях n _i ≥ 5 однородность дисперсий может быть проверена с помощью критерия Бартлета.

χ² = 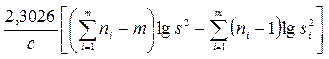, (3.13)

где

с = 1 + , (3.14)

s ² = , (3.15)

Если выполняется условие

χ² ≤ χ²_α (3.16)

для выбранного уровня значимости α и числа степеней свободы k = m – 1, то нулевую гипотезу о равенстве генеральных дисперсий совокупностей, из которых взяты выборки, не отвергают. В противном случае – отвергают и принимают альтернативную гипотезу.

В случае подтверждения нулевой гипотезы, на основании выражения (3.15) производят новую оценку генеральной дисперсии σ².

 

 

Критерий равенства средних значений двух нормально распределённых совокупностей

 

 

Если дисперсии генеральных совокупностей равны, т.е. σ²₁ = σ²₂ = σ², то для проверки нулевой гипотезы а ₁ = а ₁ = а вычисляют оценку дисперсии σ²

s ² = . (3.17)

и статистику

t = , (3.18)

которую сопоставляют с критическим значением t _α,k (таблица 2.9), найденным для выборочного уровня значимости α и числа степеней свободы k = n ₁ + n ₂ –2. Если справедливо неравенство

| t | ≤ t _α,k, (3.19)

то нулевую гипотезу не отвергают.

Если σ²₁ ≠ σ²₂, то для проверки нулевой гипотезы а ₁ = а ₁ = а вычисляют оценку статистику

t = , (3.20)

Число степеней свободы определяют из выражения

= +

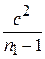где

с = ,

если выполняется неравенство (3.19) то нулевую гипотезу не отвергают.

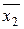Пример 3.7. Для условий примера 3.4 проверить гипотезу о равенстве средних значений. (n ₁ = 30, = 401, s ²₁ = 82; n ₂ = 20, = 409, s ²₂ = 71).

При решении примера 3.4 было показано, что гипотеза о равенстве генеральных дисперсий (σ²₁ = σ²₂ = σ²) не противоречит опытным данным. В связи с этим по формуле (3.17) находим оценку генеральной дисперсии и среднего квадратического отклонения:

s ² = 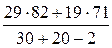= 77,6;

s = = 8,81.

По формуле (3.18) вычисляем статистику

t = = –3,15.

Задавшись α = 0,05 (для k = 30 + 20 – 2 = 48 > 30 t _α ≈ z _1–α/2), по таблице 2.8 находим критическое значение t _0,05 ≈ z _0,975 = 1,96.

В связи с тем, что условие (3.19) не выполняется, нулевую гипотезу о равенстве средних значений отвергаем.

 

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: