 |
Однофакторный дисперсионный анализ
|
|
|
|
Равенство (однородность) ряда средних значений, т.е. не значимость влияния различных технологических факторов производства полуфабрикатов и деталей, конструктивных особенностей испытуемых элементов, влияния условий испытаний и т.д. на средние значения исследуемых характеристик оценивают с помощью дисперсионного анализа результатов испытаний.
Первоначально для каждой партии вычисляют оценки среднего значения и дисперсии, после чего проверяют гипотезу об однородности ряда дисперсий. В случае подтверждения гипотезы определяют оценку общего среднего
= 
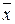, (3.21)
где m – общее число партий; 
– оценка среднего значения характеристик свойства i -й партии; n i – число образцов i -й партии.
Определяют дисперсию s 21 (межпартийная компонента) характеризующую рассеяние по факторам (число степеней свободы k 1 = m – 1)
s 21 =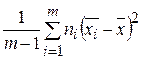 
. (3.22)
Определяют дисперсию s 22 (внутрипартийная (остаточная) компонента) характеризующую внутреннее рассеяние, связанное с неоднородностью конструкционных материалов, случайными условиями испытаний и т. д. (число степеней свободы k 2 = 
– m)
s 22 = 
. (3.23)
Проверку нулевой гипотезы о равенстве (однородности) средних проверяют с помощью критерия F.
Если дисперсионное отношение F = s 21 / s 22 окажется меньше табличного значения F 1–α, найденного для числа степеней свободы k 1 = m – 1; k 2 = – m и уровня значимости α (таблица 3.3), то исследуемые факторы не оказывают значимого влияния на исследуемые свойства, т.е. нулевая гипотеза не отклоняется. В этом случае все рассматриваемые результаты испытаний принадлежат одной генеральной совокупности, распределённой нормально с параметрами σ2 и a.
Оценкой σ2 служит выборочная полная (общая) дисперсия s 2, а оценкой а – выборочное общее среднее .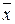
|
|
|
s 2 = 
. (3.24)
Доверительные интервалы для а и s 2 для k = – 1 степеней свободы могут быть найдены из выражений (32) и (34)
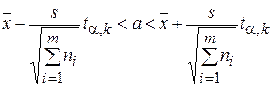, (3.25)
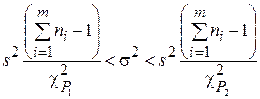. (3.26)
Если справедливо неравенство F = s 21 / s 22 > F 1–α, то нулевую гипотезу о равенстве средних значений характеристик рассматриваемых свойств отвергают.
В общем случае здесь имеется m нормально распределённых генеральных совокупностей с общей дисперсией σ2 и разными средними значениями а i. Оценкой генеральной дисперсии σ2 является величина s 22, оценками генеральных средних а i – выборочные средние . Доверительные интервалы для σ2 и а i для k = – m степеней свободы определяют на основании выражений, аналогичных формулам (3.25) и (3.26):
, (3.25)
. (3.26)
Степень вариации генеральных средних характеристик рассматриваемых свойств отдельных совокупностей, вызванная влиянием уровня исследуемого фактора, оценивается с помощью статистики
σ2 a = 
, (3.27)
называемой дисперсией значений. Это название является условным, так как генеральные средние а 1, а 2,…, а i,…, аm представляют собой детерминированные величины, а не случайные.
Дисперсия σ2 a является количественной характеристикой стабильности технологического процесса по исследуемым свойствам.
Выборочную дисперсию средних значений (оценку σ2 a) для разных объёмов отдельных партий вычисляют по формуле
s 2 a = 
(3.28)
и при n 1 = n 2 = … = n i = … = n m = n по формуле
s 2 a = (s 21 – s 22)/ n. (3.29)
Пример 3.8. По результатам испытаний провести дисперсионный анализ с целью проверки равенства средних значений
| Результаты испытаний | Объём выборки |
| s2i |
| 403; 404; 411; 403; 405; 408; 410; 407; 405; 410 413; 408; 415; 415; 416; 408 400; 400; 405; 410; 407; 403 420; 412; 406; 412; 408; 418; 416 400; 410; 415; 416; 403 421; 418; 416; 415; 410 405; 406; 405; 415; 401 425; 421; 415; 420; 419; 416 408; 410; 419; 400; 403 428; 421; 409; 418; 413 408; 418; 416; 416; 415; 410 420; 418; 425; 406; 413 403; 405; 418; 410; 407; 405; 410 412; 406; 412; 408; 418 412; 416; 402; 408; 408 | 406,6 412,5 404,2 414,6 408,8 416,0 406,4 419,3 408,0 417,8 413,8 416,4 408,3 411,2 409,2 | 9,16 13,10 15,77 16,95 50,70 16,50 26,80 13,07 53,50 53,70 15,37 52,30 25,24 21,20 27,20 |
|
|
|
Учитывая, что в каждой партии число образцов n i ≥ 5 и объёмы выборокнеодинаковые, проверку однородности дисперсий производим по критерию Бартлета
По формуле (3.13) вычисляем статистику
χ2 =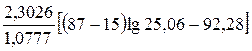 
= 11,6337,
где с = 1 +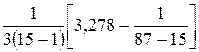 
= 1,0777;
s 2 = 
= 25,06.
В таблице 2.10 для α = 0,01 и числа степеней свободы k = m – 1 = 14
χ20,01 = 29,1
Условие (3.16) выполняется
χ2 = 25,06 < χ20,01 = 29,1
Следовательно дисперсии можно считать однородными.
Оценку генерального среднего производим по формуле (3.21)
= 
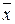= 411,33.
Межпартийная компонента дисперсии (3.22) (число степеней свободы k 1 = m – 1 = 14)
s 21 = 
= 126,39.
Внутрипартийная (остаточная) компонента дисперсии (3.23) (число степеней свободы k 2 = – m = 87 – 15 = 72)
s 22 = 
= 25,4
Дисперсионное отношение
F = s 21 / s 22 = 4,974.
Меньше табличного (таблице 3.3)
В этом случае все рассматриваемые результаты испытаний принадлежат одной генеральной совокупности, распределённой нормально с параметрами
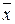= 411,33.
s 2 = 25,06.
|
|
|
