 |
Критерии согласия. Проверка гипотез о виде функции
|
|
|
|
Распределения
В одних случаях закон распределения может быть установлен теоретически на основании выбранной модели рассматриваемого процесса. В других случаях функцию распределения выбирают априорно. Однако для получения надёжных решений вероятностных задач в каждом отдельном случае необходима проверка соответствия опытных данных используемому закону распределения.
Наиболее простым, но весьма приближённым методом оценки согласия результатов эксперимента с тем или иным законом распределения является графический метод. Опытные данные сравнивают с графиком принятой функции распределения. Если экспериментальные точки ложатся вблизи кривой со случайными отклонениями влево и вправо, то опытные данные соответствуют рассматриваемому закону. Данный способ является субъективным и используется на практике лишь в качестве первого приближения.
Критерий согласия Пирсона (χ2) применяют для проверки гипотезу о соответствии эмпирического распределения предполагаемому теоретическому распределению при большом объёме выборки (n ≥ 100). Критерий применим для любых видов функций, даже при неизвестных значениях их параметров.
Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) n j для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.
Число интервалов зависит от объёма выборки. Обычно принимают: при n = 100 e = 10 … 15, при n = 200 e = 15 … 20, при n = 400 e = 25 … 30, при n = 1000 e = 35 … 40.
Интервалы, содержащие менее пяти наблюдений объединяют с соседними.
Статистикой критерия Пирсона служит величина
|
|
|
χ2 =  , (3.30)
, (3.30)
где p j – вероятность попадания изучаемой случайной величины в j -й интервал, вычисляемая в соответствии с гипотетическим законом распределения. При вычислении вероятности p j нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. Например, при нормальном распределении первый интервал простирается до –∞, а последний – до +∞.
Если выполняется неравенство
χ2 ≤ χ2α, (3.31)
при уровне значимости α и числе степеней свободы k = e – m – 1, (m – число параметров, оцениваемых по рассматриваемой выборке, для нормального закона распределения m = 2), то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.
Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы. В связи с этим рекомендуется дополнять проверку соответствия распределения по критерию χ2 другими критериями. Особенно это необходимо при сравнительно малом объёме выборки (n ≈ 100).
Пример 3.9. Проверить с помощью критерия согласия χ2 гипотезу о нормальном распределении данных в примере 2.2. Принять уровень значимости α = 0,05.
Оценка вероятности попадания значения характеристики в интервал (6-ой столбец) представляет собой разность значений функций Лапласа на правой и левой границе интервала. Если интервалы объединяются, вычисляют разность значений функции на границах объединённого интервала. Сумма чисел p j в 6 столбце всегда будет равна единице. Сумма в 7 столбце должна равняться сумме в 3-м столбце.
Таблица 3.6
| j | Границы интервала x j | Число наблюдений n j | Координаты границ интервалов
 = = 
| Значение функции Лапласа на границе интервала
Ф( ) )
| Оценка вероятности попадания в интервал p j | np j | 
|
| 5,825; 5,975 | –∞; –1,24 | 0,000; 0,1075 | 0,1075 | 10,75 | 0,984 | ||
| 5,975; 6,125 | |||||||
| 6,125; 6,275 | –1,24; –0,76 | 0,1075; 0,2236 | 0,1161 | 11,61 | 0,223 | ||
| 6,275; 6,425 | –0,76; –0,29 | 0,2236; 0,3859 | 0,1623 | 16,23 | 0,643 | ||
| 6,425; 6,575 | –0,29; 0,19 | 0,3859; 0,5753 | 0,1894 | 18,94 | 0,224 | ||
| 6,575; 6,725 | 0,19; 0,67 | 0,5753; 0,7486 | 0,1733 | 17,33 | 0,006 | ||
| 6,725; 6,875 | 0,67; 1,14 | 0,7486; 0,8729 | 0,1243 | 12,43 | 0,198 | ||
| 6,875; 7,025 | 1,14; 1,61 | 0,8729; 0,9463 | 0,0734 | 7,34 | 0,244 | ||
| 7,025; 7,175 | 1,61; ∞ | 0,9463; 1,0000 | 0,0537 | 5,37 | 0,025 | ||
| 7,175; 7,325 | |||||||
| 7,325; 7,475 | |||||||
| Сумма | – | – | 1,0000 | χ2 = 2,547 |
|
|
|
Для α=0,05 и k = 8 – 2 –1 = 5(8 – число интервалов после объединения, 2 – число параметров, оцениваемых по выборке (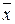 , s))
, s))
χ2 = 2,547 < χ20,05 =11,1
Заключение: опытные данные не противоречат нормальному закону распределения.
Таблица 3.7 – Значение нормированной функции нормального распределения (функции Лапласа)
| z | Сотые доли z | |||||||||
| 0,0 | 0,50000* | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | ||||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | ||||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | ||||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 | ||||||||||
| 4,0 | – | – | – | – | – | |||||
| Примечание. Ф(– z) = 1 – Ф(z) * У всех остальных значений функции Лапласа разряд целых также равен нулю, и поэтому в таблице приведены только десятичные знаки |
Приложение А
|
|
|
|
|
|


