Главная | Обратная связь | Поможем написать вашу работу!

Общие задачи по курсу лекций за 1-7недели

1. С некоторой высоты над поверхностью земли вертикально вниз брошено тело с начальной скоростью 5 м/с. Какой вид имеет уравнение зависимости скорости тела от времени?

2. Пассажирский катер проходит расстояние 150 км по течению реки за 2 часа, а против течения за 3 часа. Скорость катера в стоячей воде равна?

3. Вы растягиваете пружину, прикладывая механическое усилие: сначала двумя руками за противоположные концы, а затем, прикрепив один конец к стене, тянете за другой двумя руками. Одинаково ли растянется пружина?

4. Вычислите количество теплоты, выделившейся в результате абсолютно неупругого, центрального соударения двух шаров массами 1 кг и 2 кг, двигавшихся со скоростью 2 м/с и 1 м/с соответственно. Шары движутся навстречу друг другу.

5. Чему равна молярная масса воды (в системе СИ)?

6. Какой температуре по шкале Цельсия соответствует температура Т=267 К?

7. Чему равна сила тока при коротком замыкании с ЭДС 12 В и внутренним сопротивлением 0,1 Ом?

8. Чему равна индуктивность контура, если при силе тока 2 А в нем Существует магнитный поток 8 Вб?

9. Заряженная частица с зарядом q движется перпендикулярно однородному магнитному полю со скоростью v. Как изменится радиус траектории движения частицы с зарядом в 2 раза больше, при сохранении всех других параметров?

10. Уравнение гармонических колебаний материальной точки имеет вид: . Какая из физических величин определяет начальную фазу колебательного движения?

11. На сколько изменяется фаза колебаний за время одного полного колебания?

12. Дайте характеристику изображения, полученного собирающей тонкой линзой, если предмет находится между главным фокусом и оптическим центром.

13. Можно ли с помощью рассеивающей линзы получить увеличенное изображение предмета? Если да, то где его можно расположить?

14. Каков состав атома?

15. Общая формула, выражающая правило смещения при а-распаде?

Неделя 8-15

Задание 3

I_C

I_LR

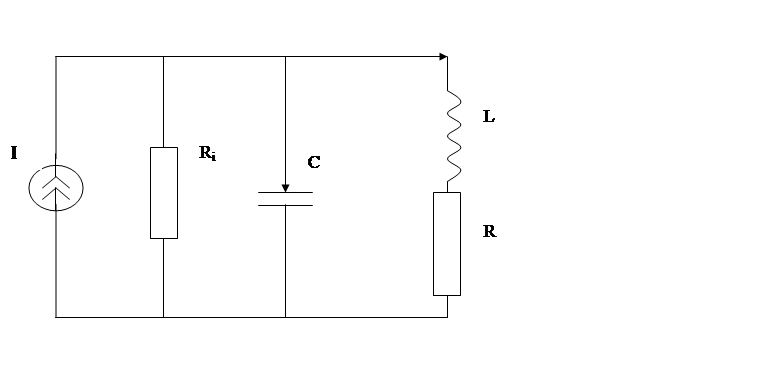
Параметры электрической цепи:

L = 1.25·10^-4Гн

С = 0,5·10^-9Ф

R = 45 Ом Rn = R₀

R₀ = 5,556·10³ – 7,133j R_i = 27780 – 49,665j

1. определить резонансную частоту, резонансное сопротивление, характеристическое сопротивление, добротность и полосу пропускания контура.

Резонансная частота ω₀ = 3,984·10⁶ (вычисления произведены в MATCAD 5.0)

Резонансное сопротивление:

Характеристическое сопротивление ρ в Омах

Добротность контура

Полоса пропускания контура

Резонансная частота цепи

ω₀ = 3,984·10⁶

Резонансное сопротивление цепи

Добротность цепи: Qцепи = 0,09.Полоса пропускания цепи

Рассчитать и построить в функции круговой частоты модуль полного сопротивления:

3. Рассчитать и построить в функции круговой частоты активную составляющую полного сопротивления цепи:

4. Рассчитать и построить в функции круговой частоты реактивную составляющую полного сопротивления цепи:

5. Рассчитать и построить в функции круговой частоты АЧХ комплексного коэффициента передачи по току в индуктивности:

6. Рассчитать и построить в функции круговой частоты ФЧХ комплексного коэффициента передачи по току в индуктивности:

7. Рассчитать мгновенное значение напряжение на контуре:

Ucont = 229179·cos(ω₀t + 90˚)

8. Рассчитать мгновенное значение полного тока на контуре:

Icont = 57,81cos(ω₀t + 90˚)

9. Рассчитать мгновенное значение токов ветвей контура:

I_LR = 646cos(ω₀t + 5˚)

I_C= 456,5cos(ω₀t - 0,07˚)

Определить коэффициент включения Rn в индуктивную ветвь контура нагрузки с сопротивлением Rn = Ro, при котором полоса пропускания цепи увеличивается на 5%.

Данную схему заменяем на эквивалентную в которой параллельно включенное сопротивление Rn заменяется сопротивлением Rэ включенное последовательно:

Выполняя математические операции используя программу MATCAD 5.0 находим значение коэффициента включения K_L:

Задание 4

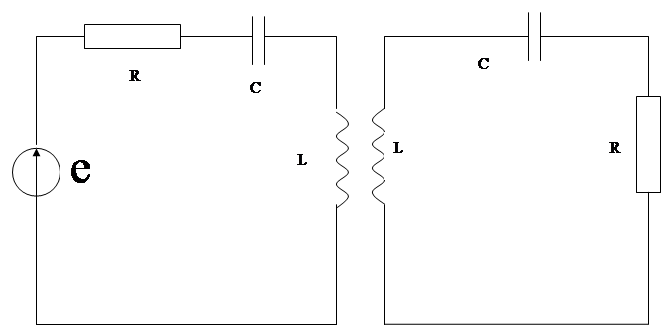
Параметры цепи:

e(t) = 90sinωt = 90cos(ωt - π_/2)

Q = 85

L = 3.02 · 10^-3Гн

С = 1,76 • 10^-9 Ф

Рассчитать параметры и частотные характеристики двух одинаковых связанных колебательных контуров с трансформаторной связью, первый из которых подключен к источнику гармонического напряжения.

1. определить резонансную частоту и сопротивление потерь R связанных контуров:

2. Рассчитать и построить в функции круговой частоты АЧХ И ФЧХ нормированного тока вторичного контура при трех значениях коэффициента связи Ксв = 0.5Ккр (зеленая кривая на графике), Ксв = Ккр (красная кривая на графике), Ксв = 2Ккр (синяя кривая на графике), где Ккр – критический коэффициент связи.

ФЧХ нормированного тока вторичного контура при трех значениях коэффициента связи Ксв = 0.5Ккр (зеленая кривая на графике), Ксв = Ккр (красная кривая на графике), Ксв = 2Ккр (синяя кривая на графике), где Ккр – критический коэффициент связи.

Графически определить полосу пропускания связанных контуров при коэффициенте связи Ксв = 0,5Ккр

Графически определить полосу пропускания связанных контуров при коэффициенте связи Ксв = Ккр

Графически определить полосу пропускания связанных контуров при коэффициенте связи Ксв = 2Ккр, а так же частоты связи.

Задание5

Рассчитать переходный процесс в электрической цепи при включении в нее источника напряжения e(t) амплитуда которого равна E = 37 и временной параметр Т = 0,46 мс, сопротивление цепи R = 0.9 кОм, постоянная времени τ = 0.69.

Определить индуктивность цепи, а так же ток и напряжение на элементах цепи

Гн

Так как данная цепь представляет собой последовательное соединение элементов, ток в сопротивлении и индуктивности будет одинаковым следовательно для выражения тока цепи имеем:

Исходное уравнение составленное для баланса напряжений имеет вид:

Заменяя тригонометрическую форму записи напряжения е(t) комплексной формой

Имеем:

Используя преобразования Лапласа заменяем уравнение оригинал его изображением имеем:

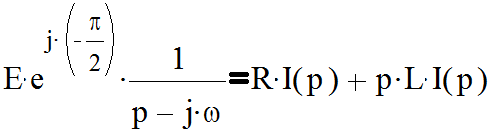Откуда

Используя обратное преобразование Лапласа находим оригинал I(t):

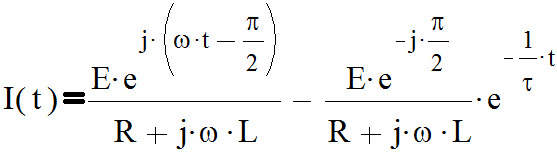Переходя от комплексной формы записи к тригонометрической имеем

Определяем напряжение на элементах цепи

Задание 6

Параметры четырехполюсника

С = 1.4 ·10^-8Ф

L = 0.001 Гн

R = 3.286 Ом

ω = 1000 рад/с

Рассчитать на частоте источника напряжения А параметры четырехполюсника:

Параметры А11 и А21 рассчитываются в режиме İ 2 = 0

Параметры А12 и А22 рассчитываются в режиме Ŭ 2 = 0

Ů2

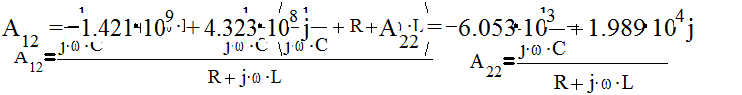
Исходная матрица А параметров четырехполюсника:

ЭЛЕКТРОСТАТИКА

1. Отрицательно заряженное тело притягивает подвешенный на нити легкий шарик, а положительно заряженное тело отталкивает. Можно ли утверждать, что шарик заряжен? Каков знак заряда?

2. Почему легкая станиолевая гильза притягивается и к положительно заряженной стеклянной палочке, и к отрицательно заряженной эбонитовой?

3. К стержню электроскопа, стоящего на изолирующей подставке, поднесли, не касаясь его, положительно заряженную стеклянную палочку. Листочки электроскопа разошлись. Затем к стержню прикоснулись пальцем другой руки. Что произойдет? Можно ли утверждать, что стержень электроскопа приобрел заряд? Какого знака? Что произойдет, если палочку теперь удалить?

4. К стержню электроскопа, стоящего на изолирующей подставке, поднесли, не касаясь его, положительно заряженную стеклянную палочку. Листочки электроскопа разошлись. Затем к стержню прикоснулись пальцем другой руки и удалили стеклянную палочку. После этого убрали палец со стержня электроскопа. Что произойдет?

5. Положительно заряженное тело притягивает подвешенный на шелковой нити легкий шарик. Можно ли утверждать, что шарик заряжен отрицательно?

6. На тонких шелковых нитях подвешены две одинаковые легкие бумажные гильзы. Одна из них заряжена, а другая — нет. Как определить, какая из них заряжена?

7. Каков знак заряда земной поверхности непосредственно под облаком, если последнее заряжено положительно?

8. Зачем верхние концы молниеотводов заостряют?

9. Увеличивает или уменьшает молниеотвод вероятность удара молнии в здание? Ответ объясните.

10. А) Положительно заряженный шар А (рис. 11О) поместили вблизи металлического шара В. Измерения показали, что сила электрического взаимодействия шаров равна нулю. Заряжен ли шар В?

С) Докажите, что если заряд шара В будет положительным и очень небольшим, то шары А и В будут не отталкиваться, а притягиваться.

11. Найдите силу взаимодействия между положительным и отрицательным точечными зарядами 1мкКл, находящимися на расстоянии 10 см.

12. С какой силой взаимодействуют два точечных заряда 10 нКл и 15 нКл, находящиеся на расстоянии 5 см друг от друга?

Рис 1. 13. На каком расстоянии находятся друг от друга точечные заряды 2нКл и 5 нКл, если они взаимодействуют друг с другом с силой 9 мН?

14. Два точечных одинаковых заряда взаимодействуют друг с другом с силой 0,4 мН, находясь на расстоянии 5 см друг от друга. Чему равен каждый заряд?

15. Найдите силу взаимодействия двух точечных электрических зарядов 1 нКл и 4 нКл в пустоте и керосине, если расстояние между ними 2 см.

16. Два одинаковых шарика, заряженные один отрицательным зарядом—1,5 мкКл, другой положительным 25 мк К,л, приводят в соприкосновение и вновь раздвигают на расстояние 5 см. Определите заряд каждого шарика после соприкосновения и силу их взаимодействия.

17. Два одинаковых металлических маленьких шарика заряжены так, что заряд одного из них в 5 раз больше заряда другого. Шарики привели в соприкосновение и раздвинули на прежнее расстояние. Во сколько раз изменилась по модулю сила их взаимодействия, если: А) шарики заряжены одноименно; С) шарики заряжены разноименно?

18. Одинаковые металлические шарики, заряженные одноименно зарядами q и 4q, находятся на расстоянии х друг от друга. Шарики привели в соприкосновение. На какое расстояние надо их раздвинуть, чтобы сила взаимодействия осталась прежней?

19. Докажите, что если два одинаковых металлических шарика, заряженные одноименно неравными зарядами, привести в соприкосновение и раздвинуть на прежнее расстояние, сила взаимодействия обязательно увеличится, причем тем значительнее, чем больше различие в значении зарядов.

20. Шарик массой 150 мг, подвешенный на топкой непроводящей нити, имеет заряд 10 нК.л. На расстоянии 32 см. Снизу под ним располагают второй заряженный шарик. Каким должен быть заряд этого шарика, чтобы сила натяжения нити: А). уменьшилась вдвое; С). увеличилась вдвое.

Постоянный ток

Определите общее сопротивление цепи, изображенной на рисунках 137, 138, 139.
Определите сопротивление однородного проволочного каркаса в форме правильного шестиугольника с двумя диагоналями, соединенными в центре (рис. 140). Сопротивление

каждой стороны шестиугольника принять равным R.

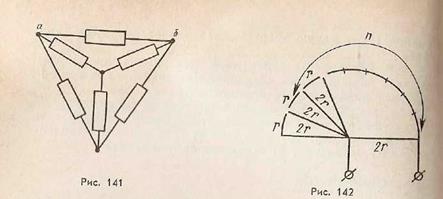
3. Провода соединены по схеме, изображенной на рисунке 141. Сопротивление каждого из проводов равно 1 Ом. Чему равно сопротивление Raв между точками а и в?

4. Определите сопротивление цепи, изображенной на рисунке 142.

5. На рисунке 143 показаны два разных способа включения в цепь реостата. Перечислите особенности работы реостата в каждом случае. Каково максимальное сопротивление каждого участка цепи, если сопротивление каждого резистора равно Ю

6. На рисунке 144 показан способ включения реостата в цепь, как потенциометра. С какой целью прибегают к такому включению?

7. На рисунке 145 изображены схемы устройств, называемых ламповыми реостатами. Объясните принцип действия этих реостатов. Есть ли преимущества у какого-либо из приведенных реостатов перед другим? Какие?

8. Удлинитель длиной 30 м сделан из медного провода диаметром 1,3 мм. Каково сопротивление удлинителя? Каково падение напряжения на нем, если по нему течет ток 10 А?

9. Определите сопротивление нити лампы (рис. 146). если вольтметр показывает 50 В, амперметр показывает 0,5 А и внутреннее сопротивление вольтметра равно 40 кОм.

10. Две дуговые лампы и добавочный резистор соединены последовательно и включены в сеть напряжением ПО В. Зайдите сопротивление добавочного резистора, если падение напряжения на каждой лампочке 40 В, а сила тока в цепи 12 А.

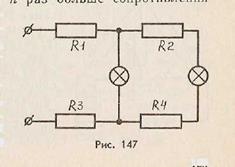
11. К источнику тока напряжением 12 В присоединена линия, питающая две лампы. Схема включения ламп показана на рисунке 147. Сопротивление участков линии Rx = = R2 — R3 — R4, = R " 1,5 Ом. Сопротивление каждой лампы 36 Ом. Определите падение напряжения па каждой лампе.

12. Сопротивление одного из двух последовательно включенных проводников в

другого. Во сколько раз изменится сила тока на участке (напряжение постоянно), если эти проводники включить параллельно?

13. Три одинаковые лампочки соединены по схеме, приведенной на рисунке 148. Как будет изменяться накал каждой из ламп, если эти

16. Как движется точка, если кинематическое уравнение движения: х=5t+20?

17. Как изменится потенциальная энергия упруго деформированного тела при уменьшении его деформации в 2 раза?

18. Тело плотностью плавает в жидкости плотностью . На какую часть своего объема погружено тело?

19. Температура газа была 300 К и возросла на 8 %. Какова стала температура газа?

20. Как изменится температура газа при адиабатном сжатии?

21. Спирт испаряется при постоянной температуре С. Поглащается или выделяется при этом энергия?

22. Физическая величина, являющаяся энергетической характеристикой электростатического поля?

23. Как следует изменить расстояние между точечными зарядами, чтобы сила взаимодействия между ними уменьшилась в 3 раза?

24. При переходе луча света из первой среды во вторую, угол падения равен , а угол преломления . Чему равен относительный показатель преломления второй среды относительно первой?

25. Груз массой m поднимают из состояния покоя на высоту h с постоянным ускорением а. Чему равна работа силы, вызывающей перемещение?

26. При какой температуре находился газ в закрытом сосуде, если при нагревании его на 140 К давление возросло в 1,5 раза?

27. Лампочки, сопротивление которых 3 и 12 Ом, поочередно подключенные к некоторому источнику тока, потребляют одинаковую энергию. Найдите внутреннее сопротивление источника тока.

28. Какова энергия магнитного поля катушки, индуктивностью 200 мГн, при силе тока в ней, равной 2 А?

29. Уравнение гармонических колебаний материальной точки имеет вид: 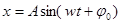. Используя это уравнение, найдите выражение, определяющее ускорение точки в начальный момент времени.

30. Энергетический выход реакции – это…

Тестовые задания

001. Какому закону надежности (P(t)=?) соответствует постоянное значение интенсивности отказов (λ(t)=const).

А) Экспоненциальному

С) Степенному

С) Логарифмическому

D) Линейному

E) Синусоидальному

002. Может ли работоспособный объект быть неисправным.

A) Нет

B) Да

C) Вопрос не имеет смысла

D) Однозначный ответ невозможен

E) В период капитального ремонта

003. Назовите свойство объекта, которое в зависимости от назначения объекта и условий его применения состоит из сочетаний свойств: безотказности, долговечности, ремонтопригодности и сохраняемости.

A) Надежность

B) Наработка

C) Предельное состояние

D) Исправность

E) Ресурс

004. Назовите свойство объекта непрерывно сохранять работоспособность в течение некоторой наработки или в течение некоторого времени.

A) Безотказность

B) Долговечность

C) Ремонтопригодность

D) Сохраняемость

E) Дублирование

005. Назовите свойство объекта сохранять работоспособность до наступления предельного состояния с необходимыми перерывами для технического обслуживания и ремонта.

A) Долговечность

B) Ремонтопригодность

C) Безотказность

D) Сохраняемость

E) Резервирование

006. Назовите свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению отказов и повреждений, к восстановлению работоспособности и исправности в процессе технического обслуживания и ремонта.

A) Ремонтопригодность

B) Долговечность

C) Безотказность

D) Сохраняемость

E) Резервирование

007. Назовите свойство объекта непрерывно сохранять исправное и работоспособное состояние в течение (и после) хранения и (или) транспортирования.

A) Сохраняемость

B) Долговечность

C) Ремонтопригодность

D) Резервирование

E) Безотказность

008. Можно ли один и тот же объект в зависимости от условий его эксплуатации в одних случаях считать восстанавливаемым, в других – невосстанавливаемым.

A) Вопрос не имеет смысла

B) Однозначный ответ невозможен

C) Да

D) Нет

E) При достижении предельного состояния

009. В каких случаях ЭВМ можно рассматривать как невосстанавливаемый объект.

A) ЭВМ в бухгалтерии при расчете заработной платы

B) Бортовая ЭВМ метеоспутника на заводском стапеле

C) ЭВМ для домашних компьютерных игр

D) Управляющая ЭВМ АСУ ТП

E) Бортовая ЭВМ метеоспутника во время космического полета

010. Релеевскому закону распределения времени наработки на отказ соответствует….

A) Постоянная интенсивность отказов

B) Степенная интенсивность отказов

C) Логарифмическая интенсивность отказов

D) Линейно возрастающая интенсивность отказов

E) Синусоидальная интенсивность отказов

011. Классическая кривая λ(t) имеет несколько характерных участков. Укажите их число.

A) 2

B) 3

C) 4

D) 5

E) 6

012. Вероятность безотказной работы системы с последовательным соединением элементов (в смысле надежности) и независимыми их отказами определяется…..

A) Произведением вероятностей безотказной работы всех элементов системы

B) Суммой вероятностей безотказной работы всех элементов системы

C) Вероятностью отказа наименее надежного элемента

D) Вероятностью безотказной работы наименее надежного элемента

E) Вероятностью безотказной работы наиболее надежного элемента

013. Вероятность отказа системы с параллельным соединением элементов (в смысле надежности) и независимыми их отказами определяется…..

A) Произведением вероятностей безотказной работы отдельных элементов

B) Произведением вероятностей отказов отдельных элементов

C) Вероятностью отказа наименее надежного элемента

D) Вероятностью отказа наиболее надежного элемента

E) Вероятностью безотказной работы наиболее надежного элемента

014. В теории надежности переход системы из одного состояния в другое представляется марковским случайным процессом. Чье имя носит система дифференциальных уравнений для определения вероятностей нахождения системы в том или ином состоянии.

A) Эйнштейна

B) Максвелла

C) Ома

D) Колмогорова

E) Релея

015. Площадь, ограниченная кривой вероятности безотказной работы невосстанавливаемого объекта и осями координат, численно равна.….

A) Средней наработке до отказа

B) Средней интенсивности отказов

C) Вероятности отказа

D) Плотности распределения наработки до отказа

E) Вероятности безотказной работы

016. Приемник к началу наблюдения за отказами проработал 100 часов. К концу наблюдения наработка составила 700 часов. Всего зарегистрировано 6 отказов. Среднее время ремонта составило 10 часов. Определить наработку на отказ и коэффициент готовности.

A) 50 часов и 0,25

B) 100 часов и 0,91

C) 100 часов и 1,1

D) 150 часов и 15

E) 4800 часов и 1,5

017. Один из основных показателей надежности восстанавливаемых объектов определяется следующим образом: удельное число отказов в единицу времени на один образец аппаратуры (на один объект). Назовите этот показатель.

A) Вероятность безотказной работы

B) Частота отказов

C) Интенсивность отказов

D) Параметр потока отказов

E) Средняя наработка на отказ

018. Назовите параметр надежности, характеризующий надежность элемента в каждый данный момент, т.е. его локальную надежность: число отказов в единицу времени, отнесенное к среднему числу элементов, безотказно работающих в данный промежуток времени (при этом отказавшие элементы не заменяются.

A) Интенсивность отказов

B) Частота отказов

C) Вероятность безотказной работы

D) Вероятность отказа

E) Средняя наработка до отказа

019. Размеченный граф дублированной системы состоит из трех узлов-состояний 1, 2, 3 расположенных горизонтально слева направо (схема «гибели и размножения»), двух верхних ветвей-стрелок перехода из первого состояния (обе системы работоспособны) во второе состояние (одна система отказалА) и из второго состояния в третье состояние (обе системы отказали), двух нижних ветвей-стрелок перехода из третьего состояния во второе состояние и из второго состояния в первое состояние. Верхние стрелки характеризуют деградацию дублированной системы, а нижние – ее восстановление. Интенсивность отказа одной системы – λ. Интенсивность восстановления одной системы одним ремонтником – μ.

Какой режим работы и какая стратегия обслуживания реализована в данном графе:

2λ λ

μ μ

A) Дублированная система с горячим резервом и одним ремонтником

B) Дублированная система с горячим резервом и двумя ремонтниками, каждый из которых обслуживает свой элемент

C) Дублированная система с холодным резервом и одним ремонтником

D) Дублированная система с холодным резервом и двумя ремонтниками, каждый из которых обслуживает свой элемент

E) Дублированная система с холодным резервом и двумя ремонтниками, которые в случае отказа двух элементов восстанавливают каждый свой элемент, а при отказе одного элемента оба восстанавливают отказавший.

020. Размеченный граф дублированной системы состоит из трех узлов-состояний 1, 2, 3 расположенных горизонтально слева направо (схема «гибели и размножения»), двух верхних ветвей-стрелок перехода из первого состояния (обе системы работоспособны) во второе состояние (одна система отказалА) и из второго состояния в третье состояние (обе системы отказали), двух нижних ветвей-стрелок перехода из третьего состояния во второе и из второго состояния в первое состояние. Верхние стрелки характеризуют деградацию дублированной системы, а нижние – ее восстановление. Интенсивность отказа одной системы – λ. Интенсивность восстановления одной системы одним ремонтником – μ.

Какой режим работы и какая стратегия обслуживания реализована в данном графе:

2λ λ

μ 2μ

A) Дублированная система с горячим резервом и одним ремонтником

B) Дублированная система с горячим резервом и двумя ремонтниками, каждый из которых обслуживает свой элемент

C) Дублированная система с холодным резервом и одним ремонтником

021. Размеченный граф дублированной системы состоит из трех узлов-состояний 1, 2, 3 расположенных горизонтально слева направо (схема «гибели и размножения»), двух верхних ветвей-стрелок перехода из первого состояния (обе системы работоспособны) во второе состояние (одна система отказалА) и из второго состояния в третье состояние (обе системы отказали), двух нижних ветвей-стрелок перехода из третьего состояния во второе и из второго состояния в первое состояние. Верхние стрелки характеризуют деградацию дублированной системы, а нижние – ее восстановление. Интенсивность отказа одной системы – λ. Интенсивность восстановления одной системы одним ремонтником – μ.

Какой режим работы и какая стратегия обслуживания реализована в данном графе:

λ λ

μ μ

A) Дублированная система с горячим резервом и одним ремонтником

B) Дублированная система с горячим резервом и двумя ремонтниками, каждый из которых обслуживает свой элемент

C) Дублированная система с холодным резервом и одним ремонтником

022. Размеченный граф дублированной системы состоит из трех узлов-состояний 1, 2, 3 расположенных горизонтально слева направо (схема «гибели и размножения»), двух верхних ветвей-стрелок перехода из первого состояния (обе системы работоспособны) во второе состояние (одна система отказалА) и из второго состояния в третье состояние (обе системы отказали), двух нижних ветвей-стрелок перехода из третьего состояния во второе и из второго состояния в первое состояние. Верхние стрелки характеризуют деградацию дублированной системы, а нижние – ее восстановление. Интенсивность отказа одной системы – λ. Интенсивность восстановления одной системы одним ремонтником – μ.

Какой режим работы и какая стратегия обслуживания реализована в данном графе:

λ λ

μ 2μ

A) Дублированная система с горячим резервом и одним ремонтником

B) Дублированная система с горячим резервом и двумя ремонтниками, каждый из которых обслуживает свой элемент

C) Дублированная система с холодным резервом и одним ремонтником

023. Размеченный граф дублированной системы состоит из трех узлов-состояний 1, 2, 3 расположенных горизонтально слева направо (схема «гибели и размножения»), двух верхних ветвей-стрелок перехода из первого состояния (обе системы работоспособны) во второе состояние (одна система отказалА) и из второго состояния в третье состояние (обе системы отказали), двух нижних ветвей-стрелок перехода из третьего состояния во второе и из второго состояния в первое состояние. Верхние стрелки характеризуют деградацию дублированной системы, а нижние – ее восстановление. Интенсивность отказа одной системы – λ. Интенсивность восстановления одной системы одним ремонтником – μ.

Какой режим работы и какая стратегия обслуживания реализована в данном графе:

λ λ

2μ 2μ

A) Дублированная система с горячим резервом и одним ремонтником

B) Дублированная система с горячим резервом и двумя ремонтниками, каждый из которых обслуживает свой элемент

C) Дублированная система с холодным резервом и одним ремонтником

024. Система S может находиться в одном из трех возможных состояний S1, S2, S3. Предельные вероятности этих состояний равны 0,2; 0,3 и 0,5 соответственно. Сколько часов в среднем система S будет находиться в состояниях S1, S2, S3 после перехода к установившемуся режиму (t → ∞) за время наблюдения в 200 часов.

A) 40, 60 и 100 часов соответственно

B) 20, 120 и 60 часов соответственно

C) 50, 70 и 80 часов соответственно

D) 60, 50 и 90 часов соответственно

E) 10, 30 и 160 часов соответственно

025. Для какого закона надежности имеет место следующее утверждение: вероятность безотказной работы объекта в течение заданного промежутка времени не зависит от того, сколько времени он проработал до этого промежутка, т.е. приработка, старение и изнашивание в этом законе не учитываются.

A) Логарифмический

B) Экспоненциальный

C) Релеевский

D) Синусоидальный

E) Гиперболический

026. Как называется случайный процесс, протекающий в системе, если он обладает следующими свойствами: для каждого момента времени t0 вероятность любого состояния системы в будущем, т.е. при t > t0, зависит только от ее состояния в настоящем, т.е. при t = t0, и не зависит от того, когда и каким образом система пришла в это состояние, т.е. как развивался процесс в прошлом.

A) Колмогоровский

B) Ньютоновский

C) Марковский

D) Максвелловский

E) Гауссовский

027. Какого типа случайные процессы в основном рассматриваются в теории надежности.

A) С непрерывными состояниями и непрерывным временем

B) С непрерывными состояниями и дискретным временем

C) С дискрет

⇐ Предыдущая 6 7 8 9 10 11 12 13 1415

Воспользуйтесь поиском по сайту: