 |
Средняя медиана и мода для объединенных групп
|
|
|
|
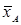- среднее для каждого класса, 
- количество учащихся
Среднее общее группы:
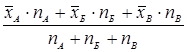
Для определения моды и медианы объединенной группы необходимы конкретные значения измерений.
Мода – это такое число в группе, с которым совпадает наибольшее количество значений в группе.
Медиана – это такая точка на числовой оси, для которой сумма абсолютных значений разности всех значений меньше суммы разностей для любой другой точки. Если именно так определять понятие ошибки, то медиана дает минимальную ошибку. Если же ошибка определяется как сумма квадратов разностей, то минимальную ошибку дает среднее.
Выбор меры центральной тенденции
· В малых группах мода очень нестабильна;
· На медиану не влияет величины очень больших и очень малых значений;
· На величину среднего влияет каждое значение;
· Некоторые множества данных не имеют меры центральной тенденции. Такая ситуация близка к бимодальной гистограмме или U -образной;
· Центральная тенденция групп, содержащая крайние значения наилучшим образом представляется в том случае, если гистограмма унимодальна;
· Если гистограмма симметрична и унимодальна, то средняя мода и медиана совпадают.
Другие меры центральной тенденции
Среднее геометрическое: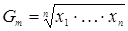 
; Среднегармоническое: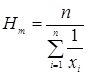 
Меры изменчивости – второй момент характеризующий данные
Для оценки меры неоднородности (разброса, изменчивости), в группе вводят специальные меры, с помощью которых после их исследования можно уменьшить изменчивость данных. Первая из мер изменчивости называется размахом.
Размах – это разность максимального и минимального значений в группе.
Включающий размах – это разность между естественной верхней границей интервала, включая наибольшее значение, и естественной нижней границей, включая наименьшее значение интервала. 
. Включающий размах отличается от исключающего на единицу.
|
|
|
Размах от 90-го до 10-го процентеля: D = P 90 – P 10. Эта мера более стабильна, чем предыдущая, так как на нее влияет множество значений.
Полу-междуквантильный размах: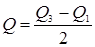 
, Q используется в распределениях, которые симметричны относительно медианы и среднего, для корректировки границ.
Дисперсия. Каждая из предыдущих мер возрастает с ростом рассеяния и уменьшается однородностей. Дисперсию, в отличие от предыдущих мер, используют при вычислении каждого из полученных измерений. Вычисляются значения отклонений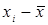 
и чтобы при суммировании 
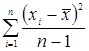не потерять величины этих отклонений, разница возводится в квадрат, поскольку мы оцениваем отклонение каждого измерения, делим на количество измерений. Обозначается дисперсия как 
.
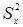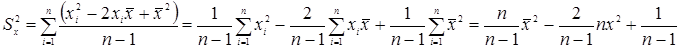
Для вычисления дисперсии не нужно вычислять среднее.
Дисперсия при сгруппированных данных вычисляется по такой же формуле, но 
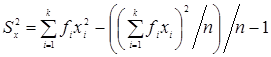
i изменяется от 1 до k, где k – количество разных значений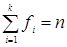 
.
Стандартное отклонение: 
Для унимодальных симметричных распределений почти 70% значений лежит в интервале 
.
Свойства дисперсии:
1. Влияние на дисперсию увеличения каждого значения на какую либо константу:
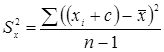, после выполнения математических операций убеждаемся, что дисперсия не изменяется.
2. Изменение дисперсии при умножении каждого исходного значения на константу:
, то есть дисперсия увеличивается на квадрат константы.
3. Дисперсия объединенной группы:
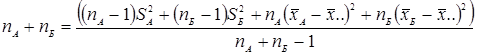
где:
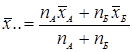
- количество значений группы А, для Б аналогично
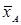- среднее группы А, для Б аналогично
Среднее отклонение – это совокупность отклонений каждого значения от среднего, взятого по модулю:
|
|
|
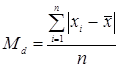
Очень проста в вычислениях, но редко используется, ввиду того, что нет теоретического обоснования.
Стандартизованные данные
Часто появляется потребность оценить положение какого-либо конкретного значения по отношению к среднему в единицах стандартного отклонения
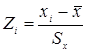
Любое множество данных можно преобразовать в такое множество, у которого среднее равно нулю, а стандартное отклонение равно единице.
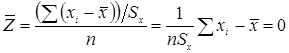
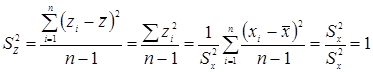
Значение стандартизованных данных Z позволяют преобразовать множество x в произвольную шкалу с удобными характеристиками среднего и стандартизованного отклонения. Сами оценки Z могут быть отрицательными или содержать дроби. Мы избавимся от этих шероховатостей, умножая стандартизованные данные на константу и прибавляем к ним константу.
с z – будет иметь стандартное отклонение
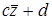, где с, d – константы – будут иметь среднее равное d.
Третий момент
Асимметрия – это свойство распределения частот. На практике симметричные полигоны и гистограммы не встречаются и чтобы выявить и оценить степень асимметрии, вводят следующую меру:
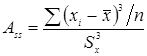
В единицах стандартного отклонения асимметрия равна:
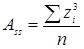
Асимметрия бывает положительной и отрицательной. Положительная сдвигается влево, а отрицательная – вправо.
Чтобы упростить вычисление Ass можно использовать следующую формулу:
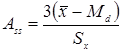
Асимметрия в этом уравнении принимает значения от –3 до +3
Четвертый момент
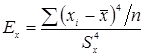
Эксцесс – это мера крутости кривой распределения. Унимодальная кривая распределения может быть островершинной, плосковершинной, средне вершинной.
Эксцесс для стандартных данных:
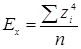
| Характер распределения | Величина эксцесса |
| Нормальное Островершинное Плосковершинное | 3 больше 3 и может быть очень большим больше нуля, но меньше 3 |
Эти четыре момента составляют набор особенностей распределения при анализе данных.
Нормальное распределение
Нормальное распределение лучше всего описывается кривой созданной ДеМуавром по следующей формуле:
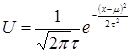
где U – высота кривой над осью x, t и μ – числа, которые определяют положение кривой относительно числовой оси и регулируют ее размах. Для μ=0, t =1 график принимает вид:
|
|
|
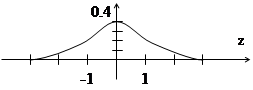Эта кривая при μ=0, t =1 получила статус стандарта, ее называют единичной нормальной кривой, то есть любые собранные данные стремятся преобразовать так, чтобы кривая их распределения была максимально близка к этой стандартной кривой. Созданы статистические таблицы со значениями площади под единичной нормальной кривой влево от любой точки на оси z в (-3; 3). Общая площадь под кривой равна 1. И все остальные площади рассматривают как процент от целого.
Свойства нормальных кривых:
Семейство нормальных кривых включают в себе все кривые, которые можно получить по данной формуле, отличающиеся друг от друга только парой значений t и μ.
1. 68% площади лежит в интервале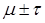 
2. 95% площади лежит в интервале 
3. 99,7% площади лежит в интервале 
Если x имеет нормальное распределение со средним μ и стандартным отклонение t, то z равное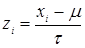 
характеризуется распределением со средним равным нулю и стандартным отклонением равным 1. Площадь между двумя значениями x в нормальном распределении равна площади между ux стандартизованными величинами в единичном нормальном распределении. Нормализованную кривую изобрели для решения задач теории вероятности, но оказалось на практике, что она отлично аппроксимирует распределение черт при большом числе наблюдений для множества переменных. Можно предположить, сто не имея материальных ограничений на количество объектов и время проведения эксперимента, статистическое исследование приводило к нормально кривой.
|
|
|
