 |
Двумерное нормальное распределение
|
|
|
|
Если при исследовании появляется вопрос о связи между двумя переменными для одного и того же объекта (например, рост и интеллект) мы говорим о двумерных связях и результаты эксперимента находят свое отражение в двумерном распределении частот.
Уравнение поверхности называется двумерным нормальным распределением (гладкая непрерывная колоколообразная поверхность)
Характеристики нормального распределения
· Распределение значений x без учета значений y есть нормальное распределение;
· Распределение значений y без учета значений x, тоже нормальное распределение;
· Для каждого фиксированного значения x значение y дают нормальное распределение с дисперсией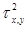 
;
· Для каждого фиксированного значения y значение x распределяется нормально с дисперсией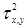 
;
· Среднее значения y для каждого отдельного значения x ложатся на переменную.
Меры изменчивости
При решении вопроса о наличии взаимосвязи (корреляции) между двумя переменными, руководствуются несколькими коэффициентами. Связь, выраженная графически, называется диаграммной рассеивания, где x – оценка IQ, y – оценка теста по математике.
Положение каждого объекта на диаграмме распределения определяется парой значений xi, yi и выражаются по отношению к мере центральной тенденции величинами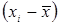 
, 
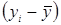. Если объект имеет высокие показатели по обеим переменным, то эти величины получаются большими и положительными, в противном случае, если xi, yi малы, то разность большой и отрицательной.
В дальнейшем будем говорить о произведении этих разностей и в том случае когда наблюдается прямая связь между этими переменными, произведение будет большим и положительным, следовательно такой же будет и сумма этих произведений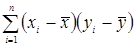 
.
|
|
|
В случае обратной связи, когда большим значениям yi соответствуют малые значения xi и наоборот, в этом случае произведение разностей будет большим и отрицательным и сумма разностей также будет большой и отрицательной.
Если между переменными не наблюдается какой-либо связи, количество положительных и отрицательных произведений примерно рано и сумма их близка к нулю. Таким образом большая положительная сумма – жесткая прямая зависимость; большая отрицательная сумма – сильная обратная зависимость; близость к нулю – отсутствие зависимости.
Недостатком этой меры является то, что ее величина зависит от числа пар переменных x участвующих в расчетах.
Чтобы избежать связь независимого состояния V групп, мы усредняем эти значения:
- ковариация
Частный случай, ковариация переменной с самой сабой – дисперсия
Чтобы избавить меру связи от отклонений двух групп значений:
- коэффициент кореляции Пирсона или произведение моментов.
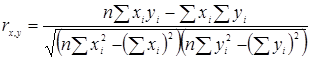
Значение коэффициента Пирсона не может выйти за границы интервала (-1; 1).
Влияние линейного преобразования переменных на коэффициент кореляции
Вместо xi вводим в формулу bx + a, где a, b – коэффициенты, для yi вводим в формулу dy + c, где c, d – коэффициенты.
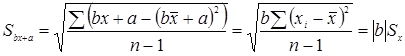
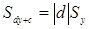
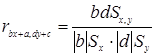
Вопрос о кореляции между переменными будучи решен положительно не означает наличия более общего вида связи (заработная плата учителям и количество поступивших в ВУЗы после окончания школы). Если мы проводим идентификацию групп с различным средним, наличие кореляции не исключено, но возможно другое объяснение взаимосвязи, чем вытекающее их эксперимента. Отсутствие связи при нулевом коэффициента Пирсона означает всего лишь отсутствие линейной связи.
Дисперсия суммы и разности переменных
|
|
|
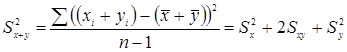
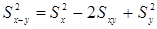
Предсказание и оценивание
Переменная, которую мы хотим оценить называется зависимой переменной или откликом, обозначим ее через y.
Переменная которую мы используем для оценки называется независимой переменной или фактором, ее обозначим через x.
Конкретная характеристика (переменная x) имеющаяся в нашем распоряжении, позволяет получить до проведения эксперимента значение y, зависимой переменной. Мы получаем 
используя xi и коэффициенты b 1 и b 0.
Даже при наилучшем линейном предсказании, предсказание 
будет отличаться от реального yi на какую-то величину, которую мы назовем ошибкой оценки и обозначим ei:
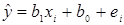
Точность предсказания зависит от того, насколько удачно подобраны коэффициента b 1 и b 0. Критерием успешности подбора коэффициентов является минимальная величина суммы квадратов всех ошибок оценки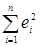 
– критерий наименьших квадратов
Другой критерий: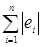 
. Этот критерий приводит к медианой линии регрессии. Из уравнения 
следует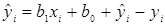 
Исходя из минимизации формулы наименьших квадратов найдем формулы:
; 
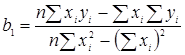Наше исследование получается наиболее результативным, если мы предполагаем, что фактор и отклик имеют двумерные нормальные распределения.
С войства двумерного нормального распределени я
1. Выборочные средние отклика (y) для каждого значения x лежат на прямой;
2. Для любого значения x, соответствующие значения y нормально распределены;
3. Для любого значения x, y – имеют одинаковую дисперсию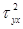 
.
При прогнозировании является ли среднее ошибок оценки подходящей мерой для прогнозирования.
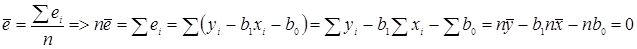
Средняя ошибка оценки всегда равна нулю. Один из способов доказать этот факт, это выбрать в качестве меры прогнозирования дисперсию ошибки оценки.
Стандартная ошибка оценки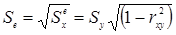 
Стандартную ошибку оценки применяют для определения пределов, в окрестности предсказанного 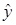попадает фактическое значение yi.
В приделах Se – расположено 69% фактических значений объекта, в приделах 2 Se – 95%, в приделах 3 Se – 97,5%.
Связь b 1 и b 0 с другими описательными статистиками
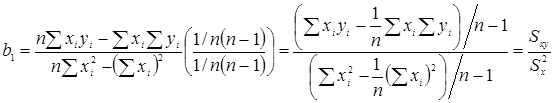
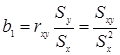
Если x и y распределены по нормальному закону и имеют одинаковую дисперсию, то 
.
|
|
|
Поскольку rxy не зависит от Sx и Sy, b 1 - принимает максимальное значение при rxy =1 и минимальное значение при rxy = -1, следовательно b 1 никогда не может быть больше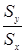 
, при rxy =1 и не может быть меньше 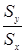при rxy = -1.
Если между переменными отсутствует линейная связь, b 1 =0 уравнение регрессии сводится к прямой без наклона, то есть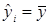 
.
|
|
|
