 |
Формулы равноускоренного вращения.
|
|
|
|
Если угловое ускорение  постоянно, то
постоянно, то



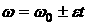
и угол поворота




 и
и  – угловая скорость и угол поворота тела в начальный момент
– угловая скорость и угол поворота тела в начальный момент 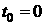 ,
,
 и
и  – в момент времени
– в момент времени  . При ускоренном вращении в уравнениях - выбирается знак «+», а при замедленном – знак «-».
. При ускоренном вращении в уравнениях - выбирается знак «+», а при замедленном – знак «-».
Вопрос 12. Момент инерции тел.Теорема Штейнера.
Момент инерции - величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Момент инерции (I или J) – зависит от массы, и размеров тела, от выбора оси вращения.
Момент инерции материальной точки относительно оси вращения - произведение массы этой точки на квадрат расстояния от оси.

Момент инерции твердого тела - это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.
Формула момента инерции:

Единица измерения СИ: кг·м².
Обозначение: I или J.
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиуса R | Ось цилиндра | mR2 |
| Сплошной цилиндр (диск) радиуса R | Ось цилиндра | 1/2mR2 |
| Шар радиуса R | Ось проходит через центр шара | 2/5mR2 |
| Прямой тонкий стержень длины L | Ось перпендикулярна к стержню и проходит через его середину | 1/12mL2 |
| Прямой тонкий стержень длины L | Ось параллельна стержню | mR2 |
Теорема Штейнера
Формулировка. Момент инерции относительно произвольной оси определяется как момент инерции относительно параллельной оси, проходящей через центр масс + произведение массы тела на квадрат расстояния между данной осью и осью, проходящей через центр масс.


Вопрос 13. Момент силы. Момент импульса.
Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
|
|
|
Размерность - [Н⋅м] (Ньютон на метр) либо кратные значения [кН⋅м]


Если:
M — момент силы (Ньютон · метр),
F — Приложенная сила (Ньютон),
r — расстояние от центра вращения до места приложения силы (метр),
l — длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр),
α — угол, между вектором силы F и вектором положения r,
То
| 2. | M = F·l = F·r·sin (α) |
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количествовращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Материальная точка
Момент импульса  материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора иимпульса:
материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора иимпульса:

где  — радиус-вектор, проведенный из точки O,
— радиус-вектор, проведенный из точки O,  — импульс материальной точки.
— импульс материальной точки.
Твердое тело (ТТ)
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:

где  — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как 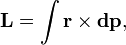 где
где  — импульс бесконечно малого точечного элемента системы).
— импульс бесконечно малого точечного элемента системы).
Частная формула для ТТ, если ось вращения неподвижна
 , J – момент инерции, w – угловая скорость
, J – момент инерции, w – угловая скорость
Вопрос 14.Основной закон динамики вращательного движения.
Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела
|
|
|
 ,
,
где F – сила, приложенная к телу массой m; а – линейное ускорение тела.
Если к твердому телу массой m в точке А (рис. 5) приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение  и соответственные линейные ускорения, как если бы на каждую точку действовала сила
и соответственные линейные ускорения, как если бы на каждую точку действовала сила  . Для каждой материальной точки можно записать:
. Для каждой материальной точки можно записать:
 ,
,
где  , поэтому
, поэтому
 , (1.7)
, (1.7)
где mi – масса i- й точки;  – угловое ускорение; ri – ее расстояние до оси вращения.
– угловое ускорение; ri – ее расстояние до оси вращения.
Умножая левую и правую части уравнения (1.7) на ri, получают
 , (1.8)
, (1.8)
где 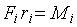 – момент силы – это произведение силы
– момент силы – это произведение силы  на ее плечо
на ее плечо  .
.
Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы  .
.

Рис. 5. Твердое тело, вращающееся под
действием силы F около оси “ОО”
 – момент инерции i -й материальной точки.
– момент инерции i -й материальной точки.
Выражение (1.8) можно записать так:
 . (1.9)
. (1.9)
Просуммируем левую и правую части (1.9) по всем точкам тела:
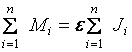 .
.
Обозначим  через М, а
через М, а  через J, тогда
через J, тогда
 (1.10)
(1.10)
Уравнение (1.10) – основной закон динамики вращательного движения твердого тела. Величина  – геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение
– геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение  .
.  – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».
– алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».
Мгновенное значение углового ускорения  , есть первая производная угловой скорости
, есть первая производная угловой скорости  по времени
по времени 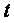 , то есть
, то есть
 , (1.11)
, (1.11)
где  – элементарное изменение угловой скорости тела за элементарный промежуток времени
– элементарное изменение угловой скорости тела за элементарный промежуток времени  .
.
Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то
 или
или  , (1.12)
, (1.12)
где  – импульс момента силы – это произведение момента силы
– импульс момента силы – это произведение момента силы  на промежуток времени
на промежуток времени  .
.
 – изменение момента импульса тела,
– изменение момента импульса тела,  – момент импульса тела есть произведение момента инерции J на угловую скорость
– момент импульса тела есть произведение момента инерции J на угловую скорость  , а
, а  есть
есть  .
.
Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы  , действующий на вращательное тело, равен изменению его момента импульса
, действующий на вращательное тело, равен изменению его момента импульса  ”:
”:
 или
или 
Вопрос 15.Энергетические характеристики при вращательном движении.
|
|
|
1) Работа.
Рассмотрим работу, совершаемую внешней силой при вращении твердого тела. Пусть сила направлена по касательной к окружности, по которой движется точка приложения силы. Тогда сила параллельна перемещению. Элементарная работа равна:
 , (10.95)
, (10.95)
где  - угловое перемещение, соответствующее движению по окружности радиуса
- угловое перемещение, соответствующее движению по окружности радиуса  ;
;  - момент силы относительно оси
- момент силы относительно оси  . Так как направлении оси
. Так как направлении оси  и угловой скорости
и угловой скорости  совпадают, то
совпадают, то
 .
.
2) Энергия.
Если рассматриваем движение относительно мгновенной оси.

Выделяем движение центра масс и вращения относительно центра масс.
Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс (центра инерции) и кинетической энергии вращательного движения тела относительно мгновенной оси)*, т.е

Вопрос 16.Момент импульса. Закон сохранения момента импульса. Закон сохранения механической энергии.
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
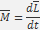
Если M=0,то  = 0 => L = const.
= 0 => L = const.
M=0 – т.к условие сохранение момента импульсов (сумма моментов внешних сил равна = 0, моментов импульсов отдельных тел (частей тела)

В проекции на ось:


Вопрос 17.Описание движения в неинерциальной системе отсчета.Силы инерции. Запись 2-го закона Ньютона для материальной точки в НИСО.
Чтобы описать движение тел в неинерциальной системе отсчета, необходимо указать способ определения сил инерции. В инерциальной системе отсчета уравнение движения тела имеет вид  . С учетом сил инерции в неинерциальной системе отсчета это уравнение примет вид
. С учетом сил инерции в неинерциальной системе отсчета это уравнение примет вид  . Отсюда
. Отсюда 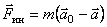 . Разность ускорений
. Разность ускорений  равна ускорению, с которым неинерциальная система отсчета движется относительно инерциальной. Это ускорение иногда называют переносным. Таким образом, выражение для сил инерции в движущейся прямолинейно неинерциальной системе отсчета имеет вид
равна ускорению, с которым неинерциальная система отсчета движется относительно инерциальной. Это ускорение иногда называют переносным. Таким образом, выражение для сил инерции в движущейся прямолинейно неинерциальной системе отсчета имеет вид  , то есть сила инерции направлена противоположно переносному ускорению.
, то есть сила инерции направлена противоположно переносному ускорению.
|
|
|
Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО). Основной закон динамики для неинерциальных систем отсчета:  , где
, где
 — сила, действующая на тело со стороны других тел;
— сила, действующая на тело со стороны других тел;
 — сила инерции, действующая на тело относительно поступательно движущейся НСО.
— сила инерции, действующая на тело относительно поступательно движущейся НСО.  — ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;
— ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;
 — центробежная сила инерции, действующая на тело относительно вращающейся НСО.
— центробежная сила инерции, действующая на тело относительно вращающейся НСО. 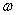 — угловая скорость НСО относительно ИСО,
— угловая скорость НСО относительно ИСО,  — расстояние от тела до центра вращения;
— расстояние от тела до центра вращения;
 — кориолисова сила инерции, действующая на тело, движущееся со скоростью
— кориолисова сила инерции, действующая на тело, движущееся со скоростью  относительно вращающейся НСО.
относительно вращающейся НСО.  — угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).
— угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).
Второй закон Ньютона будет выглядеть так: 
где aI – ускорение тела относительно неинерциальной системы отсчёта.
где 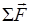 - сумма реальных сил, действующих на тело
- сумма реальных сил, действующих на тело
ПРИМЕР: Лифт  . a относительно лифта = 0
. a относительно лифта = 0
Fин + N – mg = 0
N = mg – ma
N = m(g - a)
Вопрос 22.Основные положения молекулярно-кинетической теории газа. Основное уравнение МКТ.Давление газа с точки зрения МКТ.Молекулярно-кинетичекий смысл температуры.
Основные положения МКТ:
1. Все тела состоят из молекул и атомов
2. Молекулы и атомы участвуют в хаотическом движении
3. Молекулы и атомы взаимодействуют между собой
Понятия:
1. Количество вещества – отношение числа молекул (атомов) в данном теле к числу молекул Na содержащихся в 0,012 кг углерода.
υ=N/Na
1 моль – это количество вещества, в котором число молекул (атомов)= Na
2. Молярная масса – масса одного моля данного вещества
M=Na*m0
m0 – масса одной структурной единицы вещества (молекулы, атома)
Na=6,02 *1023 моль-1 – число Авагадро.
|
|
|


