 |
Термодинамические параметры.
|
|
|
|
1) МакроПараметры
Параметры которые характеризуют термодинамическую систему на уровне наших ощущений (P, T, V)
2) Микропараметры. Параметры характеризующие однотипные свойства групп молекул. (-m0, n, Uср – средняя скорость теплового движения)
Давление – характеризует суммарное действие на окружающие тела.

 [Па]- Паскаль
[Па]- Паскаль
Запишем 2-ой закон Ньютона для потока молекул взаимодействующих со стенкой за время dt.


Где  – сила с которой молекула действует на стенку,
– сила с которой молекула действует на стенку,

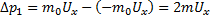

Где  учитывая хаотичный характер движения молекул (то, что в среднем половина молекул движется по направлению оси x и половина в противоположном направлении).
учитывая хаотичный характер движения молекул (то, что в среднем половина молекул движется по направлению оси x и половина в противоположном направлении).


 ,
, 
По скольку направления x,y, z равносильны и движения молекул хаотично, то можно заключить, что 




Температура.
Температура - физическая величина, характеризующая состояние теплового равновесия системы тел: все тела системы, находящиеся друг с другом в тепловом равновесии, имеют одну и ту же температуру.

Связь абсолютной шкалы и шкалы Цельсия:
T = t + 273
где t - температура в градусах Цельсия.
Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре:

Средняя квадратичная скорость молекул

Учитывая равенство (1), основное уравнение молекулярно-кинетической теории можно записать так:
p=nkT
По температуре можно судить о направлении передачи теплового движения
Вопрос 23.Статистический и термодинамический методы исследования.Термодинамическая система.Тепловое движение.Идеальный газ.Изопроцессы с идеальным газом.Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона).
Идеальный газ – модель газа, представленная следующими идеализациями:
|
|
|
1. Молекулы представляют собой маленькие упругие шарики
2. Которые не взаимодействуют друг с другом на расстоянии, а взаимодействуют только при непосредственных ударах
3. Собственным объемом молекулы принебрегают
Газ можно рассматривать, как идеальный вплоть до давления 106 Па
На основе экспериментов, проведенных учеными в 17-18 в. Были получены газовые законы. Эти законы применяются к изопроцессам
Изопроцесс – это процесс, в котором поддерживается постоянным один из макропараметров
ИЗОБАРНЫЙ ПРОЦЕСС (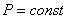 )
)
Для изобарного процесса в идеальном газе справедлив закон Гей-Люссака:
при постоянном давлении объем данной массы газа прямо пропорционален его термодинамической температуре:
 или
или  .
.
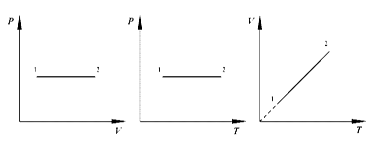
ИЗОХОРНЫЙ ПРОЦЕСС ( )
)
Изохорный процесс в идеальном газе описывается законом Шарля:
при постоянном объеме давление данной массы газа прямо пропорционально его термодинамической температуре:
 или
или  .
.

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС ( )
)
Изотермический процесс в идеальном газе подчиняется закону Бойля - Мариотта:
для данной массы газа при неизменной температуре произведение значений давления и объема есть величина постоянная:
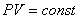 или
или  .
.

Уравнение состояния идеального газа — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа.
 , т.к
, т.к 

Так же 





Закон дальтона.
В случае смеси газов, если газы химически не взаимодействуют между собой, то каждый газ ведет себя независимо занимая весь предоставленный объем.
Уравнение состояния для смеси газов

Вопрос 24.Внутренняя энергия идеального газа.
Внутренняя энергия — это кинетическая энергия хаотического (теплового) движения частиц системы (молекул, атомов, ядер, электронов) и потенциальная энергия взаимодействия этих частиц.
В случае идеального газа взаимодействием между молекулами пренебрегаем
Wпот<<Wкин
|
|
|
U=Wкин=  (сред. Кинетическая энергия одной молекулы, зависит от структуры молекулы)
(сред. Кинетическая энергия одной молекулы, зависит от структуры молекулы)
| Идеальный газ | Число степеней свободы i | 
|
| Одноатомный газ | i=3 поступательные степени свободы | 
|
| Двухатомный газ Молекула с жесткой связью | i=3(пост)+2(вращ)=5 | 
|
| Двухатомный газ Молекула с нежесткой связью | I=3(пост)+2(вращ)+2(колеб)=7 | 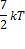
|
| Многоатомный газ | I=3(пост)+3(вращ)=6 | 
|
U=N*Wкин1= 
Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
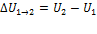
[U] – функция состояния, характеризует состояние газовой системы.
Вопрос 25.Работа и теплота. Первое начало термодинамики.
Работа газа – изменение энергии системы. Является функцией процесса
Газ оказывает давление на любую стенку сосуда. Если стенка подвижна, то сила давления F совершит работу A, переместив поршень на расстояние dl.
Если dl невелико, то давление газа останется примерно постоянным. Тогда работа будет равна:  , т.к
, т.к  .
.
Мы знаем что 

Или
Тогда A = P·(V2 - V1) = P·DV. В изобарном процессе расширения газа P = const. Следовательно, при любом сколь угодно большом увеличении объема сила давления газа на поршень будет постоянной, и формула работы сохранит свой вид
A = P·(V2 - V1).
В общем случае интеграл не посчитать, поэтому работа является функцией процесса.


Теплота – способ изменения энергии системы в результате передачи теплового движения
Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплотыδ Q, полученного телом, к соответствующему приращению его температуры δ T:

Единица измерения теплоёмкости в системе СИ — Дж/К.
Характеризует теплоемкость системы накапливать тепловую энергию.
 - функция процесса зависит от процесса перехода 1->2
- функция процесса зависит от процесса перехода 1->2
Различные теплоемкости
 (молярная)
(молярная)
С=сm=cµυ(ню)
Первое начало термодинамики
|
|
|
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил
Q = ΔU + A – Энергетический баланс
Дифференциальная формула:

 =>
=>  Работа положительна если газ расширяется
Работа положительна если газ расширяется


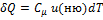

Вопрос 26.Первое начало термодинамики применительно к изопроцессам с идеальным газом.
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил
Q = ΔU + A

| Процесс | U12 | A12 | Q12 |
| Изотермический | 

|  P=
P= 
| 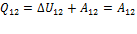
|
| Изобарный | 
| 
| 

|
| Изохорный | 
| 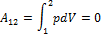
| 

|
 формула Майера
формула Майера
Вопрос 27.Адиабатный процесс. Уравнение Пуассона. Работа при адиабатном процессе.
Процесс, протекающий без теплообмена с окружающей средой.
Пример – звук.
Рассмотрим процесс быстро протекающий равновесный для выделенной газовой системы т.е процесс протекает одинаково по всему объему газа.


pV= 
dpV+pdV= 





 показатель адиабаты
показатель адиабаты





Из первого начала термодинамики следует, что работа газа при адиабатном процессе совершается за счет его внутренней энергии:

Вопрос 28.Распределение Максвелла молекул по скоростям и кинетическим энергиям.Наиболее вероятная средняя арифметическая и средняя кваратичная скорости газовых молекул.
В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был выведен теоретически Дж. Максвеллом. Максвелл предполагал, что вещество состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.
В 1860г Максвелл опираясь на законы теорий вероятности, получил функцию распределения молекул по скоростям

Максимум функции соответствует более вероятным скоростям.


 квадратичная =
квадратичная = 
Из функции распределения молекул по модулям скоростей  можно получить функцию распределения молекул по кинетическим энергиям теплового движения:
можно получить функцию распределения молекул по кинетическим энергиям теплового движения:
|
|
|
 (34)
(34)
Найдем среднюю кинетическую энергию <ε> молекулы идеального газа:

Найдем среднюю кинетическую энергию <ε> молекулы идеального газа:

Вопрос 29.Барометрическая формула. Распределение Больцмана и его смысл.
Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести
Рассмотрим на примере гравитационного поля.
Рассмотрим случай изотермический атмосферы (t=const)
Если атмосферное давление на высоте h равно р (рис. 1), то на высоте h+dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой уменьшается). Разность давлений р и p+dp равна весу газа.
Условие равновесия выделенного слоя по 2-му закону Ньютона


T=const



Выражение (1) называется барометрической формулой. Она позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту: Так как высоты считаются относительно уровня моря, где давление считается нормальным, то выражение (2) может быть представлено в виде



Выражение (2) называется распределением Больцмана для внешнего потенциального поля. Из него видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.
Если частицы находятся в состоянии хаотического теплового движения и имеют одинаковую массу и, то распределение Больцмана (2) применимо в любом внешнем потенциальном поле, а не только в поле сил тяжести
Вопрос 30.Число столкновений и средняя длина свободного пробега молекул. Эффективный диаметр молекул.
Средняя длина свободного пробега молекулы(<λ>)- это среднее расстояние, которое проходит молекула между двумя последовательными ударами с другими молекулами.

где –  средняя скорость теплового движения ,< τ > – среднее время между двумя столкновениями.
средняя скорость теплового движения ,< τ > – среднее время между двумя столкновениями.

Модель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между собой только при столкновении. Обозначим <σ >– эффективное сечение молекулы, характеризующее столкновение между двумя молекулами.

 – площадь, в которую не может проникнуть центр любой другой молекулы. Здесь
– площадь, в которую не может проникнуть центр любой другой молекулы. Здесь  – диаметр молекулы. За одну секунду молекула проходит путь, равный средней арифметической скорости
– диаметр молекулы. За одну секунду молекула проходит путь, равный средней арифметической скорости 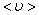 . За ту же секунду молекула претерпевает ν столкновений. Следовательно,
. За ту же секунду молекула претерпевает ν столкновений. Следовательно,

Эффективный диаметр молекулы- минимальное расстояние, на которое сближаются при столкновении центры двух молекул. При столкновении молекулы сближаются до некоторого наименьшего расстояния, которое условно считается суммой радиусов взаимодействующих молекул. Столкновение между одинаковыми молекулами может произойти только в том случае, если их центры сблизятся на расстояние, меньшее или равное диаметру d - эффективному диаметру молекулы.
|
|
|

Число столкновений(<ν>)
Вероятность столкновения трех и более молекул бесконечно мала.
Предположим, что все молекулы застыли, кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d
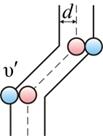
Путь, который пройдет молекула за одну секунду, равен длине цилиндра  . Умножим объём цилиндра
. Умножим объём цилиндра  на число молекул в единице объёма n, получим среднее число столкновений в одну секунду:
на число молекул в единице объёма n, получим среднее число столкновений в одну секунду:
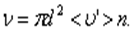
На самом деле, все молекулы движутся (и в сторону, и навстречу друг другу), поэтому число соударений определяется средней скоростью движения молекул относительно друг друга.
По закону сложения случайных величин:

А так как средняя длина свободного пробега  , то получим:
, то получим:

Уравнение состояния идеального газа позволяет нам выразить n через давление P и термодинамическую температуру Т.
Так как  , то есть
, то есть  ,то
,то

Таким образом, при заданной температуре средняя длина свободного пробега обратно пропорциональна давлению Р:

Вопрос 31. Явление переноса:диффузия, вязкость, теплопроводность.
1)Диффузия- явление переноса вещества.
Уравнение стационарной диффузии:
Рассматриваем явление выравнивания плоскости
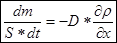
 -масса, переносимая между слоями, в единицу времени, через площадь S.
-масса, переносимая между слоями, в единицу времени, через площадь S.
 -градиент плотности в направлении оси X(изменение плотности по направлению оси Х).
-градиент плотности в направлении оси X(изменение плотности по направлению оси Х).
 -коэффициент диффузии.
-коэффициент диффузии.
 -средняя длина свободного пробега.
-средняя длина свободного пробега.
 -средняя тепловая скорость.
-средняя тепловая скорость.


 «-» - в уравнении означает, что вещество переносится в сторону убыли плотности.
«-» - в уравнении означает, что вещество переносится в сторону убыли плотности.
 |
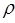 1 <
1 < 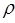 2<
2< 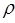 3
3
2)Вязкость(Внутреннее трение) - явление переноса упорядоченного движения между слоями.

 - ко эффициент вязкости(«эта»)
- ко эффициент вязкости(«эта»)

 -плотность
-плотность
 -градиент скорости(показывает, как изменяется скорость от одного слоя к другому)
-градиент скорости(показывает, как изменяется скорость от одного слоя к другому)






 «-» -означает, что сила трения направлена противоположно направлению возрастания скорости.
«-» -означает, что сила трения направлена противоположно направлению возрастания скорости.




|
 |

3)Теплопроводность -явление переноса теплового движения.

 -время
-время

 -коэффициент теплопроводности
-коэффициент теплопроводности
 -удельная теплоемкость при постоянном объеме
-удельная теплоемкость при постоянном объеме
Тепловой поток направлен в сторону, противоположную возрастанию температуры.
Вопрос 32.Макроскопческие процессы(хаотические и упорядоченные).Термодинамические процессы(обратимые и необратимые).
|
|
|



