Свойства и параметры полупроводниковых p-n-переходов

 

Полупроводниковые (ПП) материалы на основе p-n переходов из кремния (Si=30%) или германия (Ge), либо арсенид галлия (GaAs) применяют при производстве диодов, транзисторов, аналоговых и цифровых интегральных МС. (О=47%).

p-n переход – это контакт 2-х ПП, обладающих разным типом проводимости, где катодная n -областьлегирована донорной примесью(Li ^– ), создающей высокую концентрацию электронов (доноров N_D), а анодная p -областьлегирована акцепторной примесью(In⁺), создающей высокую концентрацию акцепторов (N_А).

p-n- переход служит основой ПП элементов, обладающих односторонней проводимостью тока. *Примечание. См. табл. Менделеева: (Li^– №3), (In⁺ №49).

Электропроводность (s) p-n -перехода зависит от направления приложенного тока: высокая – для прямого движения тока и низкая – для обратного движ. тока.

Удельная электропроводность ПП: σ = (1/ρ) = 10 ^–8 ÷10 ⁵ [1 / (Ом ∙ мм² / м)] = [1 / Ом ∙ м].

В равновесном состоянии высота потенциального барьера (контактная разность потенциалов φ_К [1]) между p и n – областями ПП определяется выражением:

 

φ_К = (k·T/e)·ln( n_n · p_p /n_i²) [В]; либо φ_К = φ_Т·ln(N_A·N_D/n_i²) [В]; (1.9)

где n_n и p_p – концентрации основных носителей (электронов и дырок) n и p –области.

 

φ_Т = (k·T/e) = Т/11600 – тепловой потенциал в ПП [В]; (1.10)

k –пост. Больцмана (0,86 · 10 ^–4 эВ/К); Т –температура (К); e –заряд (1,602 · 10^–19 кл).

 

Номинальная величина: j_{К(Ge)(300К)} = 0,3÷0,45 (В); j_К(Si)(300) = 0,7÷0,8 (В).

 

Мах. контактная разность потенциалов: j_К(Ge) = 0,6÷0,7 (В), j_К(Si) = 0,9÷1,2 (В).

 

При комнатной температуре (Т = 300К) в ПП материале вся примесь ионизирована, а концентрация собственных носителей очень мала; поэтому, концентрация основных носителей равна концентрации примесей: n_n = N_D; p_p = N_A;

 

Собственная концентрация ионизированных атомов n_i в данном объеме составит:

 

n_i = N∙ e_хр^{(–DEэ/2kT)}, либо, n_i = n·p = √ N_C∙N_V ∙e_хр^(–DW/2kT), [см^-3] (1.11)

 

ΔЕ_Э = ΔW = (Eс–Еv) – ширина запрещенной зоны в полупроводнике [эВ];

ΔЕ_Э(Ge) = 0,75 (эВ); ΔЕ_Э(Si) = 1,12 (эВ);

N = √ N_C∙N_V – эффективная плотность состояний, [см^–3];

N_C – в зоне проводимости; N_V – в валентной зоне [см^–3];

 

N = 2[2p× m_o ×kT/h²]^3/2; N_С = 2[2p× m_n ^*×kT/h²]^3/2; N_V = 2[2p× m_p ×kT/h²]^3/2. (1.12)

 

Концентрация электронов (n) в зоне проводимости и дырок (р) в валентной зоне, с учетом энергии уровня Ферми (E_F), энергии верхней валентной зоны (E_V) и энергии нижней границы зоны проводимости (Е_С), составят:

 

n =N_С∙e_хр^{–(Eс–Еf)/kT}; р =N_V∙e_хр^{–(Ef–Еv)/kT}; [ n·p = N_C∙N_V∙e_хр^(–DE/kT) ]; (1.13)

 

Уровень Ферми W_F в собственном полупроводнике, соответствующий середине ширины запрещенной зоны ΔЕ_Э, составляет, например, для Si и Ge:

 

W_F1 = W_E = –ΔЕ_Э(Si)/2 = –0,56 эВ; W_E = –ΔЕ_Э(Ge)/2 = –0,37 эВ. (1.14)

Уровни Ферми в электронном (n) ПП и в дырочном (p) ПП составят:

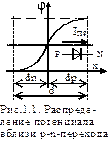W_Fn = W_E + k∙T∙ ln(N_D/ n_i ); W_Fр = W_E – k∙T∙ ln(N_A/ n_i ) (1.15)

 

Ширина p-n-перехода в равновесии (при отсутствии внешнего напряжения), составит, например, для Si:

d = (d_n + d_p) = √[(2ε_(Si)∙ε_o∙φ_k)/e]∙[(1/N_A)+(1/N_D) ], [нм]. (1.16)

 

При подаче внешнего U ширина запрещен. зоны составит:

 

Δl = d = √[(2ε_(Si)∙ε_o∙(φ_k-U)/e]∙[(1/N_A)+(1/N_D)], [нм]. (1.17)

 

где ε_(Si), ε_o – проницаемости материала и вакуума [Ф/м].

Поскольку внутри p-n-перехода общий отрицательный заряд ионизированных акцепторов равен общему положительному заряду ионизированных доноров, которые распределены на площади S поперечного сечения p-n-перехода, то d_n ∙N_D∙S = d_p ∙N_A∙S.

 

Отсюда следует: ( d_n/d_p ) = (N_A/N_D) = ( p_p/n_n ). где d_n – ширина n области (1.18)

 

Напряженность эл. поля в p-n-перех. мах-на. на границе Е_М = (2φ_К/d) [B/м] (1.19)

 

При приложении к p-n-переходу внешнего напряжения U высота потенциального барьера изменяется на величину этого напряжения:

Δφ = (φ_K – U) – разность потенциалов.

При прямых (U_ПР) напряжениях p-n-переход сужается, и при обратных (U_ОБР) напряжениях p-n-переход расширяется. (γ – коэф. свойств матер.: γ_Ge= 1,5; γ_Si = 2).

Вольтамперная характеристика (ВАХ) p-n-перехода выражает зависимость между током (I) (или плотностью тока j) через p-n-переход и приложенным напряжением U (уравнение Эберса-Молла) [1]: I =I₀(e_xp^{(U/ γ φ T)} –1); [ j = σ∙E =(1/ρ) ∙E ].

j = j_S(exp^(U/γφT)–1); j = (е∙D_n∙ n_p /L_n)+(е∙D_p∙ p_n /L_p)∙(exp^(U/γφT)–1) [A/м²]. (1.20)

j_n = е∙ n ∙μ_n∙Е; j_p = е∙ p ∙μ_p∙Е;

где j_S – плотность обратного тока насыщения [A/м²]; (γ_Ge= 1,5; γ_Si = 2);

D_n и D_р – коэф. диффузии для эл. и дырки; D_n = φ_Т∙μ_n. D_p = φ_Т∙μ_p. [cм²/c].

 

L_n и L_р – дифф-онная длины пробега эл. и дырки: L_n = √ D_nτ_n; L_p = √D_pτ_p. [cм].

n_n и р_p – концентрации основных носителей, [см ^{– 3}];

n_p и р_n – концентрации неосновных носителей, [см ^{– 3}];

τ – время жизни основных носителей [с], [nc].

 

Для невырожденных ПП концентрации неосновных носителей зарядов p_n и n_p

( дырок в электронном слое) и (электронов в дырочном слое) определяют из выражения:

 

При N_D = n_n и N_А = р_р → р_n = ( n_i ²/N_D) =( n_i ²/ n_n ), n_p = (n_i ²/N_A) = (n_i ²/ р_p) [см ^-3]. (1.21)

 

Выражение (1.20) выводится из предположения, что всё внешнее напряжение U приложено только к области p-n-перехода с проводимостью [ σ = σ_n + σ_p ].

Проводимости квазинейтральной p-области и n-области:

 

σ_p = e∙ p_p ∙μ_p, [1/Ом · м]; [ ρ_p = 1/σ_p =1/(N_A·e·μ_p) ] [Ом · м], p_p = σ_p/(e·μ_p), [см^–3], (1.22)

 

σ_n = e∙ n_n ∙μ_n, [1/Ом · м]; [ ρ_n = 1/σ_n =1/(N_Д·e·μ_n) ] [Ом · м], n_n = σ_n/(e·μ_n), [см^–3], (1.23)

 

намного больше проводимости обедненной области p-n-перехода.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: