 |
Цепь с резистивным элементом
|
|
|
|
 Резистором называется элемент электрической цепи, предназначенный для ограничения величины тока, и параметром которого является электрическое сопротивление
Резистором называется элемент электрической цепи, предназначенный для ограничения величины тока, и параметром которого является электрическое сопротивление  (l – длина проводника, S – площадь его поперечного сечения, γ – удельная электропроводность материала [2], из которого выполнен резистор). В резисторе (резистивном элементе) происходит необратимый процесс преобразования электрической энергии в тепловую.
(l – длина проводника, S – площадь его поперечного сечения, γ – удельная электропроводность материала [2], из которого выполнен резистор). В резисторе (резистивном элементе) происходит необратимый процесс преобразования электрической энергии в тепловую.
На электрических схемах резистивные элементы показываются в виде прямоугольников (рис. 13).
В цепях постоянного тока электрическое сопротивление обычно обозначают большой буквой R и иногда называют омическим в отличие от цепей переменного тока, где сопротивление резистора r называют активным. Это объясняется тем, что с увеличением частоты тока ƒ активное сопротивление r становится больше омического R из-за поверхностного эффекта, причины появления которого будут рассмотрены в следующем разделе.
На рисунке 13 показана простейшая замкнутая цепь однофазного синусоидального тока, состоящая из идеального источника э.д.с. e и резистивного элемента с активным сопротивлением r. Идеальным называется такой источник, у которого отсутствует внутреннее сопротивление [2], а, следовательно, и внутреннее падение напряжения, что позволяет считать справедливым равенство e = u, где u – выходное напряжение источника, подаваемое на вход рассматриваемой цепи. Поэтому при формулировании второго закона Кирхгофа напряжение u, подаваемое на входные зажимы цепи, должно рассматриваться в качестве э.д.с.
В дальнейшем, показанная пунктиром на рисунке 13 замыкающая часть схемы с идеальным источником э.д.с., как правило, будет опускаться, но всегда должна предполагаться существующей.
|
|
|
Предположим, что напряжение u на входе цепи изменяться по закону
|
 ,
,
то есть начальная фаза синусоиды напряжения равна нулю (ψU = 0), и на векторной диаграмме (рис. 14а) вектор амплитуды напряжения Um расположен так, что при его вращении синусоида напряжения (9) в момент времени t = 0 проходит через нулевое значение в область положительных значений (рис. 14б). Поскольку закон Ома, сформулированный для цепей постоянного тока [2], справедлив для мгновенных значений, то можно с учетом равенства (9) записать
|
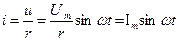 ,
,
где  – амплитуда синусоиды тока.
– амплитуда синусоиды тока.
Сравнивая правые части равенств (9) и (10) можно утверждать, что напряжение и ток в рассматриваемой цепи совпадают по фазе, поскольку их синусоиды одновременно проходят фазы положительных и отрицательных амплитуд, нулевых значений и т.п.

Рис. 14
На рисунке 14а показана векторная диаграмма амплитудных значений напряжения Um и тока Im для момента времени t = 0, а на рисунке 14б – развертка соответствующих синусоид в зависимости от времени t и фазового угла ωt. Равенство
|

представляет собой закон Ома для амплитудных значений. Разделив обе части этого равенства на  , получим выражение закона Ома для действующих (среднеквадратичных за период Т) значений тока и напряжения
, получим выражение закона Ома для действующих (среднеквадратичных за период Т) значений тока и напряжения
|
 .
.
Введем понятие о мгновенной и средней за период (активной) мощности.
|

Из выражения (13) следует, что мгновенная мощность пульсирует с двойной (по отношению к частоте сети) ч астотой 2 ω относительно среднего значения UI, оставаясь все время положительной, как это следует из графика (рис. 14в).
Средней за период (активной) мощностью называется выражение
|
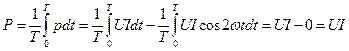 ,
,
то есть средняя (активная) мощность равна произведению действующих значений напряжения U и тока I.
|
|
|
Таким образом, в цепи с резистивным элементом r:
1. Напряжение и ток совпадают по фазе.
2. Закон Ома справедлив для мгновенных, амплитудных и действующих значений напряжения и тока.
3. Мгновенная мощность пульсирует с двойной частотой относительно среднего значения P = UI, оставаясь положительной. Это означает, что электрическая энергия все время поступает из питающей сети и необратимо преобразуется в тепловую в резисторе с сопротивлением r. Активная мощность  .
.
|
|
|


