 |
Коэффициент мощности и способы его повышения
|
|
|
|
Коэффициентом мощности называется отношение активной (средней за период) мощности Р к полной (кажущейся) мощности S.
|
Полная мощность, как это следует из треугольника мощности (рис. 29):
где Q – реактивная мощность. Кроме того, справедливы следующие соотношения: S = UI, P = UIcosφ, Q = UIsinφ, где U, I, φ – соответственно действующие значения напряжения и тока и угол сдвига по фазе между напряжением и током на входе потребителя переменного тока. В общем случае результирующая реактивная мощность определяется как разность индуктивной QL и емкостной QC мощностей
|
Нетрудно видеть (рис. 29), что коэффициент мощности может быть представлен как косинус угла сдвига φ между напряжением и током
|
Коэффициент мощности можно также получить как отношение активной составляющей к полной величине: сопротивления или проводимости, напряжения или тока эквивалентной последовательной и параллельной цепей, то есть
|
как это следует из соответствующих подобных треугольников.
Как известно [2], площадь поперечного сечения проводов линий электропередач и электрических сетей, обмоток электрических машин и трансформаторов выбирается из условий нагрева, то есть по величине тока I, который при заданном напряжении пропорционален полной мощности S = UI. Энергия, преобразуемая из электрической необратимо в другие виды (механическую, тепловую, химическую и др.), то есть используемая человеком для практических целей, пропорциональна активной энергии и соответствующей ей активной мощности Р, которая, как следует из выражения (58), может быть представлена в виде:
|
Поскольку U = const (стандартная величина напряжения, подаваемого на зажимы приемника), то одна и та же величина активной мощности Р может передаваться приемнику при большем токе и низком cosφ, или меньшем токе и более высоком значении коэффициента мощности cosφ.
|
|
|
Поэтому выгодно повышать cosφ на входе приемника, поскольку при этом снижается ток I в питающей линии, что позволяет увеличить ее пропускную способность, то есть передать дополнительную активную мощность, а также снизить потери напряжения на входе приемника и потери энергии на нагревание проводов линии электропередачи.
Большинство приемников электрической энергии переменного тока имеет индуктивный характер, то есть они потребляют индуктивную мощность QL (асинхронные двигатели, трансформаторы, электромагниты, выпрямители, магнитные пускатели и т.д.). Для уменьшения индуктивной мощности, передаваемой по линии, и повышения тем самым cosφ существует ряд мероприятий, в том числе искусственное повышение cosφ с помощью батареи конденсаторов, которое рассмотрим в этом разделе применительно к однофазному активно-индуктивному приемнику или одной фазе симметричного трехфазного приемника.
На рисунке 30а показана эквивалентная схема приемника, который представлен в виде двух параллельно включенных ветвей: активной r и катушки индуктивности L. Согласно первому закону Кирхгофа вектор действующее значение тока приемника 
равен геометрической сумме активного 
и индуктивного 
токов:
|
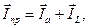
где величина тока 
.
Векторная диаграмма напряжения U питающей линии и токов эквивалентной схемы показана на рисунке 30б. Если стороны заштрихованного векторного треугольника токов умножить на напряжение U, то получится подобный исходному треугольник мощностей приемника со сторонами P, Q и S (рис. 30б)
Рис. 30
На рисунке 31а показана схема, на которой параллельно приемнику с помощью ключа K можно включить компенсирующий конденсатор с емкостью С.
|
|
|
Если ключ K разомкнут, то по питающей линии течет ток I = Iпр, чему соответствует векторная диаграмма на рисунке 30б.
Рис. 31
Чтобы уменьшить ток I линии, необходимо замкнуть ключ K (рис. 31а). При этом в цепи конденсатора потечет ток 
, опережая напряжение U на угол π /2, причем 
– емкостное сопротивление конденсатора при частоте питающей сети f = 50 Гц (ω = 2 πf – угловая частота).
Согласно первому закону Кирхгофа при замкнутом ключе K (рис. 31а)
|
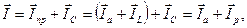
где Ip = IL – IC – реактивный ток, поступающий из сети. Соответствующая равенству (62) векторная диаграмма показана на рисунке 31б. Из диаграммы видно, что при включенном конденсаторе ток линии изменяется до величины I < Iпр, угол φ ¢ между током I в линии и напряжением U уменьшается (φ ¢ < φ), а, следовательно, коэффициент мощности увеличится (cosφ ¢ > cosφ).
Оказывается, что экономически целесообразно повышать cosφ до величины cosφ ¢ = 0,85¸0,9 при отстающем токе I, так как при достижении резонанса cosφ ¢ = 1,0 или перекомпенсации, то есть опережающем токе (φ < 0) чрезмерно повышается стоимость устанавливаемых конденсаторов.
Задача повышения cosφ обычно формулируется следующим образом: задан активно-индуктивный приемник, получающий питание от сети с напряжением U и имеющий при заданной активной мощности P = const невысокий cosφ. Необходимо рассчитать емкость компенсирующей батареи конденсаторов такой величины, чтобы коэффициент мощности установки повысился до значения cosφ ¢ > cosφ.
Можно показать, что величина емкости С при этом должна рассчитываться по формуле
|
Вывод этой зависимости приведен в [7].
Необходимо помнить, что при включении компенсирующего конденсатора (рис. 31а) сам приемник продолжает работать с тем же самым током Iпр и низким cosφ, а коэффициент мощности cosφ¢ повышается на входе всей установки, включающей сам приемник и компенсирующий конденсатор.
сть результатов расчета аналитического метода.
|
|
|
