 |
Цепь с индуктивным элементом
|
|
|
|
Индуктивность L – это параметр устройства, характеризующий способность данного устройства создавать магнитное поле, если по устройству пропустить электрический ток i.
Более строгое определение индуктивности (коэффициента самоиндукции) L можно получить из соотношения
|
где ψ – потокосцепление в веберах [Вб = В∙с];
L – индуктивность в генри [Гн = Вб/А] = [В∙с/А]= [Ом∙с];
i – сила тока в амперах [А].
Из равенства (15) следует, что индуктивность L = ψ/i – это коэффициент пропорциональности между потокосцеплением ψ и током i, который это потокосцепление создал (в соответствии с законом Ома для магнитной цепи [2]).
Индуктивностью обладают в основном катушки и обмотки, расположенные в различного вида магнитопроводах [2].
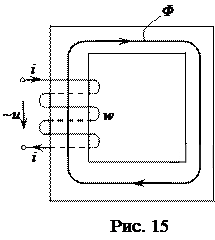
Рассмотрим идеальную катушку индуктивности с числом витков w, расположенную на замкнутом ферромагнитном магнитопроводе (сердечнике), по которой течет ток i (рис. 15). Идеальной будем считать катушку, у которой отсутствуют электрическое сопротивление обмотки (r = 0) и магнитные поля рассеяния (то есть все силовые линии магнитного потока Φ замыкаются по сердечнику, пронизывая все витки катушки). Поэтому потокосцепление идеальной катушки индуктивности можно представить в виде
|
Приравняв правые части равенств (15) и (16), получим:
|
.
В соответствии с законом Ома для магнитной цепи [2] магнитный поток 
. Сделав соответствующую подстановку в правую часть равенства (17), получим
|
где Rмагн – магнитное сопротивление ферромагнитного сердечника, зависящее от геометрических размеров сердечника и магнитной проницаемости материала, из которого он выполнен.
Как следует из равенства (18), индуктивность L идеальной катушки зависит от квадрата числа витков и магнитного сопротивления сердечника.
|
|
|
Рассмотрим схему включения идеальной катушки индуктивности в цепь синусоидального тока (рис. 16). На электрических схемах индуктивность L изображается тремя или четырьмя полуокружностями. Согласно второму закону Кирхгофа для этой цепи можно записать:
|
где u = e – мгновенное значение синусоидального напряжения u на входе цепи,
е – мгновенное значение э.д.с. идеального источника (рис. 13), который
на рисунке 16 не показан;
i – мгновенное значение тока, создающего потокосцепление ψ = Li;
ri = 0 – равное нулю падение напряжения в катушке, поскольку она
идеальна (r = 0);
– мгновенное значение э.д.с. самоиндукции.
С учетом того, что ri = 0 равенство (19) принимает вид u + eL = 0, откуда
|
то есть в каждый момент времени приложенное к цепи катушки напряжение должно быть уравновешено э.д.с. самоиндукции.
Предположим, что синусоида тока не содержит начальной фазы (ψI = 0)
|
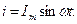
Очевидно потокосцепление в соответствии с (15)
|
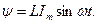
Согласно закону электромагнитной индукции [2] (в формулировке Максвелла) э.д.с. самоиндукции
|
где EmL = ωLIm – амплитуда э.д.с. самоиндукции;
sin (ωt – π/ 2) = – cosωt.
В соответствии со вторым законом Кирхгофа (20)
|
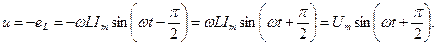
Сравнивая равенства (21) и (24), можно убедиться, что в цепи с индуктивным элементом напряжение опережает ток на четверть периода (π/ 2) или (то же самое): ток отстает от напряжения на четверть периода.
В правой части равенства (24) амплитуда напряжения Um = ωLIm, откуда
|
где xL = ωL = 2 πfL – индуктивное сопротивление, а сама зависимость (25)
представляет собой закон Ома для амплитудных значений
напряжения и тока.
Разделив обе части равенства (25) на 
, перейдем от амплитудных значений к действующим:
|
Равенство (26) представляет собой закон Ома для действующих значений.
|
|
|
Следует отметить, что правильнее считать индуктивное сопротивление xL коэффициентом пропорциональности между э.д.с. самоиндукции и током: EmL = xLIm, так как xL = ωL не является параметром (в отличие от активного сопротивления 
), поскольку зависит от частоты ω = 2 πf. Параметром является только индуктивность 
. С учетом того, что размерность xL должна быть в омах, принято называть xL индуктивным сопротивлением. Действительно: размерность угловой частоты [ ω ] = [c-1], а размерность индуктивности [ L ] = [Гн] = [Ом∙с], поэтому размерность [ xL ] = [ ω ][ L ] = [c-1] [Ом∙с+1] = [Ом].
Мгновенная мощность «р» рассматриваемой цепи – это произведение мгновенных значений напряжения и тока:
|
Средняя за период (активная) мощность
|
поскольку определенный интеграл в правой части равенства (28) дважды за период обращается в ноль.
Рис. 17
На рисунке 17а показана векторная диаграмма амплитудных значений напряжения, тока и э.д.с. самоиндукции для момента времени t = 0 с разверткой (рис. 17б) в графики соответствующих синусоид, из которых видно, например, что положительная амплитуда синусоиды тока + Im наступает позже на время Т /4по сравнению с положительной амплитудой синусоиды напряжения + Um.
На этом же рисунке видно, что согласно второму закону Кирхгофа, синусоиды напряжения и э.д.с. еL расположены в противофазе, то есть в каждый момент времени в сумме дают ноль. Здесь же можно объяснить знак «минус» в формулировке закона электромагнитной индукции по Максвеллу 
. В соответствии с принципом Ленца [2] направление индуктированной э.д.с. еL должно быть таким, чтобы препятствовать изменению тока (потокосцепления), которое вызвало эту э.д.с. Действительно, как видно из рисунка 17б, в первую четверть периода Т/4при нарастании тока i э.д.с. еL действует навстречу току, препятствуя его увеличению, а во вторую четверть периода, когда ток i начинает уменьшаться по величине, э.д.с. еL действует с током i согласно, препятствуя его уменьшению. То есть индуктивность L является инерционным звеном по аналогии с массой тела в механическом движении при ускорении и торможении.
На рисунке 17в приведен в соответствии с выражением (27) график мгновенной мощности р, которая пульсирует с двойной частотой относительно нулевого среднего значения Р = 0. Это означает, что процесс преобразования энергии в цепи с индуктивностью имеет обратимый характер (в отличие от цепи с резистивным элементом).
|
|
|
Действительно, в первую четверть периода Т/4 (рис. 17в) мгновенная мощность положительна, то есть электрическая энергия поступает из питающей сети и превращается в энергию магнитного поля Wм внутри катушки. Можно показать [1], что величина этой энергии, запасенной за четверть периода, равна
|
Во вторую четверть периода (рис. 17в) мгновенная мощность отрицательна, то есть катушка становится источником энергии, превращая энергию магнитного поля в энергию электрическую с отдачей в том же количестве обратно в питающую сеть.
Таким образом, в цепи с индуктивным элементом:
1. Ток отстает от напряжения на четверть периода (π /2).
2. Закон Ома справедлив только для амплитудных и действующих значений напряжения и тока, причем вводится понятие об индуктивном сопротивлении xL = ωL = 2 πfL.
3. Мгновенная мощность пульсирует с двойной частотой относительно нулевого значения P = 0. Это означает, что в цепи отсутствует необратимый процесс преобразования энергии, а имеет место обмен энергией между катушкой индуктивности и питающей сетью.
|
|
|
