 |
Цепь с емкостным элементом
|
|
|
|
Емкость С – это такой параметр, который характеризует способность устройства накапливать электрические заряды q, если к этому устройству приложено напряжение u.
Емкостной элемент – это идеальный конденсатор, представляющий собой две проводящие пластины площадью S, разделенные слоем диэлектрика толщиной d. Идеальным считается конденсатор, у которого проводимость слоя диэлектрика равна нулю (отсутствует ток утечки) и диэлектрическая проницаемость ε является постоянной величиной. Из школьного курса физики известна формула величины емкости идеального плоского конденсатора  .
.
Можно более строго определить емкость С как коэффициент пропорциональности между зарядом q и напряжением u, создавшим этот заряд:
|
 На электрических схемах емкостной элемент изображается двумя параллельными отрезками прямой одинаковой длины (рис. 19).
На электрических схемах емкостной элемент изображается двумя параллельными отрезками прямой одинаковой длины (рис. 19).
Если конденсатор подключить к источнику постоянного тока, то произойдет процесс его заряда, в результате чего на проводящих пластинах появится напряжение U источника, а ток зарядки прекратится, поскольку слой изоляции между пластинами постоянный ток не пропустит.
Иначе ведет себя конденсатор, когда он включен в цепь переменного тока, так как полярность напряжения на его пластинах меняется с двойной частотой питающей сети (при частоте ƒ = 50 Гц – сто раз в секунду). То есть происходит перезаряд пластин, и по проводам питающей линии протекает переменный ток, обусловленный направленным движением электронов в металлических проводниках.
Что касается слоя диэлектрика, то в нем протекает ток электрического смещения, связанный с направленной ориентацией зарядов внутри молекул диэлектрика (диполей).
|
|
|
Рассмотрим цепь синусоидального тока с идеальным емкостным элементом (рис. 19).
Предположим, что напряжение на входных зажимах цепи не содержит начальной фазы (ψU = 0),
|
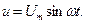
Сделаем подстановку (31) в правую часть равенства (30)
|

Как известно, электрический ток (направленное движение зарядов) в общем случае может быть представлен математически как скорость (производная) изменения заряда во времени  . С учетом зависимости (32) получим
. С учетом зависимости (32) получим
|
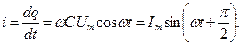
Сравнивая равенства (31) и (33), можно убедиться, что в цепи с емкостным элементом ток опережает напряжение на четверть периода (π/ 2, 90°).
В правой части равенства (33) введем обозначение Im амплитуды тока
|

где  – емкостное сопротивление. Само равенство
– емкостное сопротивление. Само равенство  представляет закон Ома для амплитудных значений тока и напряжения. Разделив обе части этого равенства на
представляет закон Ома для амплитудных значений тока и напряжения. Разделив обе части этого равенства на  , получим закон Ома для действующих значений:
, получим закон Ома для действующих значений:
|

Мгновенная мощность цепи с емкостью С:
|

Средняя за период (активная) мощность Р:
|

Таким образом, как и в цепи с идеальным индуктивным элементом, в цепи с конденсатором отсутствует необратимый процесс преобразования электрической энергии, а имеет место обмен энергией между конденсатором и питающей сетью.
На рисунке 20а приведена векторная диаграмма амплитудных значений тока Im и напряжения Um для момента времени t = 0 с разверткой в графики соответствующих синусоид (рис. 20б), а также с построением графической зависимости мгновенной мощности p= UIsin 2 ωt.
Рассмотрим подробнее обратимый процесс преобразования энергии в рассматриваемой цепи. В первую четверть периода Т/ 4(рис. 20б) мгновенная мощность положительна, то есть электрическая энергия поступает из сети, и происходит процесс зарядки конденсатора: напряжение на обкладках конденсатора возрастает от 0 до положительной амплитуды + Um, электрическая энергия превращается в энергию электрического поля [1].
|
|
|
|

Во вторую четверть периода мгновенная мощность отрицательна (p < 0), и происходит разряд конденсатора: ток меняет полярность, напряжение снижается до нуля, энергия электрического поля (38) превращается в электрическую и возвращается обратно в питающую сеть. Далее происходит аналогичный процесс со сменой полярности пластин конденсатора на противоположную и т.д

Рис. 20
Таким образом, в цепи с емкостным элементом:
1. Ток опережает напряжения на четверть периода (π /2).
2. Закон Ома справедлив только для амплитудных и действующих значений напряжения и тока. При этом вводится понятие о емкостном сопротивлении  .
.
3. Мгновенная мощность пульсирует с двойной частотой относительно среднего значения P = 0. Это означает, что процесс преобразования энергии в рассматриваемой цепи имеет обратимый характер, то есть происходит обмен энергией между конденсатором и питающей сетью.
1.4. Цепь с последовательным соединением r, L и C
На рисунке 21 показана однофазная электрическая цепь с последовательным включением резистивного r, индуктивного L и емкостного C элементов. Цепь замкнута на источник Е бесконечной мощности [2], то есть выполняется условие  (U – действующее значение синусоидального напряжения на входе цепи).
(U – действующее значение синусоидального напряжения на входе цепи).

Рис. 21
Запишем в векторной форме второй закон Кирхгофа для действующих значений напряжений применительно к рассматриваемой цепи (рис. 21):
|

Равенство (39) как второй закон Кирхгофа читается следующим образом.
В замкнутом электрическом контуре геометрическая сумма векторов действующих значений э.д.с. (в данном случае это только напряжение 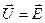 ) равна геометрической сумме векторов действующих значений падений напряжения на элементах, образующих этот контур (здесь эта сумма
) равна геометрической сумме векторов действующих значений падений напряжения на элементах, образующих этот контур (здесь эта сумма  ).
).
Поскольку в последовательной цепи (рис. 21) ток I во всех трех элементах r, L и C один и тот же, то в соответствии с законом Ома для участка цепи можно записать выражения для модулей слагаемых векторов: Ua = Ir, UL = IxL, UC = IxC. В предыдущих разделах (1.5, 1.6, 1.7) были установлены углы сдвига по фазе между вектором тока I и соответствующими падениями напряжения φa = 0, φL = + π /2, φC = – π /2, что позволяет соответствующим образом сориентировать векторы  и
и  относительно общего вектора тока
относительно общего вектора тока  и найти суммарный вектор
и найти суммарный вектор  на входе цепи (рис. 21).
на входе цепи (рис. 21).
|
|
|
Рассмотрим порядок построения векторной диаграммы последовательной цепи (рис. 21) в соответствии с равенством (39).
Ранее (рис. 14, 17 и 20) векторные диаграммы строились для амплитудных значений синусоид тока (или напряжения) применительно к моменту времени t = 0, когда исходная синусоида имела нулевую начальную фазу (ψI = 0 или ψU = 0), что позволяло эту синусоиду представлять вектором амплитудного значения в виде горизонтального вектора со стрелкой вправо (рис. 14, 17, 20).
Сохраним этот прием и для рассматриваемой цепи, задавшись синусоидой тока с нулевой начальной фазой ψI = 0:
|

где  – амплитуда тока.
– амплитуда тока.
Тогда вектор действующего значения тока I для момента времени t = 0 будет направлен, как показано на рисунке 22 а,б.
Выбрав масштаб для напряжений, изобразим векторы  с учетом углов сдвига φa = 0, φL = + π /2и φC = – π /2, совместив их начала с началом вектора
с учетом углов сдвига φa = 0, φL = + π /2и φC = – π /2, совместив их начала с началом вектора  (рис. 22а). При вращении всех четырех векторов против часовой стрелки с угловой частотой ω можно убедиться, что проходящую через центр вращения 0 «финишную ленточку», показанную на рисунке пунктиром, вначале пересекает вектор
(рис. 22а). При вращении всех четырех векторов против часовой стрелки с угловой частотой ω можно убедиться, что проходящую через центр вращения 0 «финишную ленточку», показанную на рисунке пунктиром, вначале пересекает вектор  , через четверть периода – соответствующие векторы
, через четверть периода – соответствующие векторы 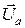 и
и  , а еще через четверть периода – вектор
, а еще через четверть периода – вектор  (соответственно φL = + π /2, φa = 0, φC = – π /2).
(соответственно φL = + π /2, φa = 0, φC = – π /2).
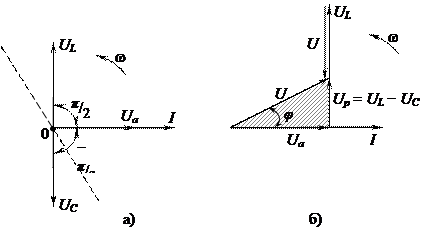
Рис. 22
Рассмотрим подробно порядок построения векторной диаграммы последовательной цепи в соответствии с равенством (39), используя известный способ сложения нескольких векторов по правилу многоугольника. Согласно этому правилу, выбрав в качестве первого слагаемого один из векторов, остальные слагаемые векторы посредством параллельного переноса совмещают началами с концами предыдущих слагаемых векторов. Соединив начало первого слагаемого вектора с концом последнего, получают суммарный вектор.
Задавшись направлением вектора  , в качестве первого слагаемого принимаем вектор
, в качестве первого слагаемого принимаем вектор 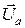 (рис. 22б). В качестве второго слагаемого строим вектор
(рис. 22б). В качестве второго слагаемого строим вектор  параллельным переносом из рисунка 22а, совместив его начало с концом вектора
параллельным переносом из рисунка 22а, совместив его начало с концом вектора 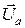 . Проделав аналогичную операцию с третьим слагаемым
. Проделав аналогичную операцию с третьим слагаемым  , получим результирующий вектор напряжения на входе цепи
, получим результирующий вектор напряжения на входе цепи  , соединив начало первого слагаемого вектора
, соединив начало первого слагаемого вектора 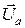 с концом третьего
с концом третьего  (рис. 22б).
(рис. 22б).
|
|
|
Очевидно полученная векторная диаграмма представляет собой графическое решение второго закона Кирхгофа, поскольку удовлетворяет уравнению (39). Как видно из векторной диаграммы на рисунке 22б, в заштрихованном векторном прямоугольном треугольнике противолежащий углу φ катет представляет собой вектор, длина которого Up равна алгебраической разности Up = UL – UC, поскольку векторы  и
и  находятся в противофазе, то есть сдвинуты на угол 180°. Результирующий вектор
находятся в противофазе, то есть сдвинуты на угол 180°. Результирующий вектор  получил название «реактивное напряжение». Поскольку UL = IxL, UC = IxC., то
получил название «реактивное напряжение». Поскольку UL = IxL, UC = IxC., то
|


где  – реактивное сопротивление.
– реактивное сопротивление.
Применив к треугольнику напряжений (рис. 22б) теорему Пифагора, получим
|

где  – полное или кажущееся сопротивление.
– полное или кажущееся сопротивление.
Перепишем равенство (42) в виде
|

которое представляет собой закон Ома для последовательной цепи, читающийся так: ток прямо пропорционален напряжению на входе цепи. Коэффициентом пропорциональности для последовательной цепи является множитель 1 /z.
Как видно из векторной диаграммы (рис. 22б) вектор напряжения  опережает вектор тока
опережает вектор тока  на угол φ (с учетом направления вращения векторов против часовой стрелки). Это объясняется тем, что в рассматриваемом случае цепь носит индуктивный характер, то есть xL > xC и UL > UC. Знак такого угла φ принято считать положительным. Очевидно для рассматриваемого случая можно записать выражение для мгновенного значения синусоиды напряжения
на угол φ (с учетом направления вращения векторов против часовой стрелки). Это объясняется тем, что в рассматриваемом случае цепь носит индуктивный характер, то есть xL > xC и UL > UC. Знак такого угла φ принято считать положительным. Очевидно для рассматриваемого случая можно записать выражение для мгновенного значения синусоиды напряжения
|

Разделив все стороны векторного треугольника напряжений (рис. 23а) на одну и ту же величину тока I, получим подобный исходному скалярный треугольник сопротивлений (рис. 23б) со сторонами
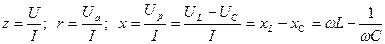 .
.
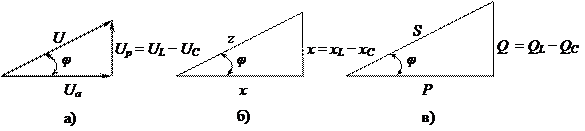
Рис. 23
Если умножить стороны треугольника напряжений на величину тока I, или стороны треугольника сопротивлений на квадрат тока I 2, то получим еще один подобный треугольник мощностей (рис. 23в) со сторонами:
Р = Ua I = I 2 r – активная мощность [Вт];
Q = Up I = I 2 x – реактивная мощность [вар];
S = U I = I 2 z – полная или кажущаяся мощность [ВА].
Как известно размерностью единицы мощности является ватт (Вт), который представляет собой произведение размерностей напряжения и тока [Вт[ = [В]×[А]. Применительно к цепям переменного тока принято различать три типа единицы мощности, хотя их размерность одна и та же:
− Вт (ватт) – единица активной (средней за период) мощности;
− вар (вольт-ампер реактивный) – единица реактивной мощности;
|
|
|
− ВА (вольт-ампер) – единица измерения полной (кажущейся) мощности.
Таким образом понятие мощности в электрической цепи синусоидального тока значительно шире, чем в цепях постоянного тока, хотя единица измерения одна и та же, а именно «ватт».
Очевидно мгновенная мощность р на входе рассматриваемой последовательной цепи равна произведению синусоиды напряжения на синусоиду тока, то есть необходимо перемножить правые части равенств (44) и (40):
|

После ряда преобразований правой части равенства (45), подробно рассмотренных в [1], можно получить выражение для мгновенной мощности в виде:
|

где P = Scosφ – активная (средняя за период) мощность;
S = UI – полная (кажущаяся) мощность (рис. 23в).
Как видно из равенства (46), мгновенная мощность р пульсирует с двойной частотой 2 ω относительно средней (активной) мощности Р, причем амплитуда косинусоиды двойной частоты  при φ ¹ 0 больше среднего значения (S > P), то есть график мгновенной мощности будет иметь отрицательные участки в пределах угла φ ¹ 0 (рис. 27б).
при φ ¹ 0 больше среднего значения (S > P), то есть график мгновенной мощности будет иметь отрицательные участки в пределах угла φ ¹ 0 (рис. 27б).
Резонанс напряжений
На стадии рассмотрения цепей с идеальными реактивными элементами: индуктивности L и емкости C − можно было предположить, что при совместном включении они будут компенсировать друг друга. Действительно, будучи включенными в последовательную цепь идеальная катушка и конденсатор создают падения напряжения UL = IxL и UC = IxC, находящиеся в противофазе и дающие результирующий вектор реактивного напряжения Up = UL – UC. Очевидно возможен случай полной взаимной компенсации реактивных элементов внутри последовательной цепи, который получил название «резонанс напряжений».
Резонансом напряжений называется такой режим работы цепи с последовательным соединением r, L и С, при котором оказываются равными друг другу индуктивное и емкостное сопротивления, то есть xL = xC.
В результате при резонансе напряжений становится справедливым следующие равенства: x = xL – xC = 0; UL = UC Þ Up = UL – UC = 0; 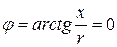 ; Þ
; Þ  Q = QL – QC = 0;
Q = QL – QC = 0; 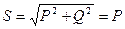 ;
;  ;
;  – ток в цепи принимает наибольшее значение. Цепь на входе ведет себя как содержащая только резистивный элемент r.
– ток в цепи принимает наибольшее значение. Цепь на входе ведет себя как содержащая только резистивный элемент r.
Сделав в правую часть равенства (46) соответствующие подстановки, а именно cosφ = 1, S = UI, φ = 0, получим выражение
|

идентичное равенству (13) для мгновенной мощности цепи с резистивным элементом.
Векторная диаграмма напряжений (UL = UC) представлена на рисунке 24. Она соответствует случаю, когда r» xL = xC. Если выполняется условие xL = xс >> r, то напряжения UL и UC будут значительно больше, чем напряжения на выходе UL = UC >> U = Ua. Это может привести к электрическому пробою изоляции реактивных элементов, а также представлять опасность для обслуживающего персонала, что необходимо учитывать при эксплуатации таких цепей.
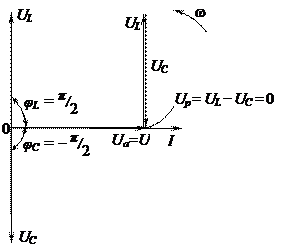
Рис. 24
1.5. Цепь с параллельным соединением r, L и C
На рисунке 25а показана разветвленная цепь с параллельным включением активного r, индуктивного L и емкостного С элементов. Особенностью такой цепи является то, что все параллельные ветви находятся под одним и тем же напряжением U, то есть работают независимо друг от друга (изменение тока одной из ветвей не влияет на токи остальных).

Рис. 25
Применим закон Ома для каждой ветви рассматриваемой схемы и введем новые обозначения:
Ток в резисторе r
 , где
, где  [Ом-1] – активная проводимость (Ом-1 = См – сименс – единица измерения проводимости [2]).
[Ом-1] – активная проводимость (Ом-1 = См – сименс – единица измерения проводимости [2]).
Ток в индуктивном элементе
 , где
, где 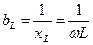 [См] – индуктивная проводимость.
[См] – индуктивная проводимость.
Ток в емкостном элементе
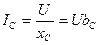 , где
, где  [См] – емкостная проводимость.
[См] – емкостная проводимость.
Составим уравнение согласно первому закону Кирхгофа в векторной форме применительно к рассматриваемой схеме (рис.25а)
|

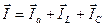 .
.
Равенство (48) читается следующим образом:
Вектор тока  , входящего в верхний узел, равен геометрической сумме векторов токов
, входящего в верхний узел, равен геометрической сумме векторов токов 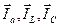 , вытекающих из этого узла.
, вытекающих из этого узла.
Задавшись масштабом тока, решим это уравнение графически в предположении, что цепь имеет емкостной характер (bC > bL Þ IC > IL).
Предположим, что синусоида напряжения имеет нулевую начальную фазу
|
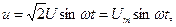
То есть вектор действующего значения напряжения  на входе цепи (рис. 25а) будет направлен аналогично вектору тока при графических построениях для последовательной цепи (рис. 22а, б).
на входе цепи (рис. 25а) будет направлен аналогично вектору тока при графических построениях для последовательной цепи (рис. 22а, б).
На рисунке 25б показано положение всех векторов при совмещении их начал в центре вращения 0, а также построена векторная диаграмма как результат сложения векторов тока в соответствии с равенством (48). Порядок построения векторной диаграммы аналогичен рассмотренному в предыдущем разделе (применительно к последовательной цепи).
Полученная векторная диаграмма (рис. 25б) представляет собой графическое решение первого закона Кирхгофа, так как удовлетворяет уравнению (48). Как видно из рисунка 25б в заштрихованном векторном треугольнике токов противолежащий углу φ катет представляет собой вектор, длина которого Ip равна алгебраической разности Ip = IC – IL, поскольку векторы 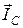 и
и 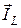 сдвинуты на 180°. Результирующий вектор
сдвинуты на 180°. Результирующий вектор  получил название «реактивный ток». Поскольку IC = UbC, IL = UbL, то
получил название «реактивный ток». Поскольку IC = UbC, IL = UbL, то
|
 ,
,
где 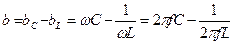 – реактивная проводимость.
– реактивная проводимость.
Применив к треугольнику токов теорему Пифагора, получим
|

где  – полная или кажущаяся проводимость.
– полная или кажущаяся проводимость.
Равенство I = Uy (51) представляет собой закон Ома для разветвленной (параллельной) цепи, читающийся так: ток в неразветвленной части цепи прямо пропорционален напряжению. Коэффициентом пропорциональности для разветвленной цепи является полная проводимость y.

Рис. 26
Разделив векторы треугольника токов (рис. 26а) на напряжение U, получим подобный исходному скалярный треугольник проводимостей (рис. 26б). Умножив стороны треугольника токов на напряжение U или стороны треугольника проводимостей на квадрат напряжения U 2, получим еще один подобный треугольник мощностей (рис. 26в) со сторонами:
P = UIa = U 2 g – активная мощность [Вт];
Q = UIp = U 2 b – реактивная мощность [вар];
S = UI = U 2 y – полная (кажущаяся) мощность [ВА].
Как видно из векторной диаграммы (рис. 25б) вектор тока  в неразветвленной части цепи опережает вектор напряжения
в неразветвленной части цепи опережает вектор напряжения  на угол φ < 0 (цепь имеет емкостной характер). С учетом заданной синусоиды напряжения (49), у которой отсутствует начальная фаза (ψU = 0), синусоида тока на входе цепи будет иметь вид
на угол φ < 0 (цепь имеет емкостной характер). С учетом заданной синусоиды напряжения (49), у которой отсутствует начальная фаза (ψU = 0), синусоида тока на входе цепи будет иметь вид
|

где  – амплитуда синусоиды.
– амплитуда синусоиды.
Мгновенная мощность на входе цепи представляет собой произведение мгновенных значений напряжения на входе цепи и суммарного тока, то есть произведение соответствующих синусоид (49) и (52)
|

Выражение (53) идентично аналогичной зависимости (46) для последовательной цепи.

Рис. 27
На рисунке 27а показана векторная диаграмма амплитудных значений напряжения  и тока
и тока 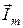 на входе цепи для момента времени t = 0 с разверткой в функции времени t и фазового угла (рис. 27б). На этом же рисунке показано построение графика мгновенной мощности в соответствии с равенством (53).
на входе цепи для момента времени t = 0 с разверткой в функции времени t и фазового угла (рис. 27б). На этом же рисунке показано построение графика мгновенной мощности в соответствии с равенством (53).
Сравнивая одинаковые фазы напряжения и тока на графиках синусоид напряжения и тока (рис. 27б), можно убедиться, что ток i на угол φ опережает напряжение u (емкостный характер нагрузки).
Для сравнения стоит обратить внимание на аналогичный рисунок (рис. 10), на котором синусоида напряжения u опережает на угол φ синусоиду тока i, что соответствует индуктивному характеру такой цепи.
Резонанс токов
Резонанс токов – это такой режим работы разветвленной цепи с параллельным включением активного, индуктивного и емкостного элементов, при котором индуктивная и емкостная проводимости равны друг другу (bL = bC).
То есть резонанс токов наступает при условии  , как и резонанс напряжений при условии
, как и резонанс напряжений при условии  . По аналогии с механическими колебательными системами резонанс токов (или напряжений) в электрической цепи синусоидального тока наступает, когда частота вынужденных колебаний f совпадает с частотой собственных колебаний f0 цепи. Частота собственных колебаний f0 цепи зависит от соотношения реактивных параметров: индуктивности L и емкости C.
. По аналогии с механическими колебательными системами резонанс токов (или напряжений) в электрической цепи синусоидального тока наступает, когда частота вынужденных колебаний f совпадает с частотой собственных колебаний f0 цепи. Частота собственных колебаний f0 цепи зависит от соотношения реактивных параметров: индуктивности L и емкости C.
Выражение для f 0 можно получить из приведенных выше равенств
|

или для собственной угловой частоты ω 0 = 2 πf 0
|

Таким образом, если требуется достичь резонанса при заданной частоте f вынужденных колебаний, в частности, при f = 50 Гц, то можно получить величину f 0 = 50 Гц посредством раздельного или совместного воздействия на индуктивность L и емкость C.
Явление резонанса в электрических цепях широко используется в технике (например, известный из школьного курса физики колебательный L – C контур).
Рассмотрим основные соотношения, характеризующие разветвленную цепь в режиме резонанса, вытекающие из соотношения bL = bC.
Полная проводимость 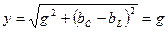 равна активной g и становится наименьшей, то есть цепь на входе ведет себя как содержащая только резистивный элемент.
равна активной g и становится наименьшей, то есть цепь на входе ведет себя как содержащая только резистивный элемент.
В соответствии с законом Ома (51) суммарный ток (на входе цепи) примет наименьшее значение

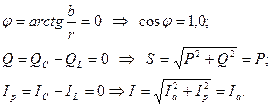
На рисунке 28 показаны векторы слагаемых токов Ia, IL, IC с учетом их сдвига относительно вектора напряжения U для случая резонанса тока (IL = IC) и построение векторная диаграмма в соответствии с первым законом Кирхгофа (48).
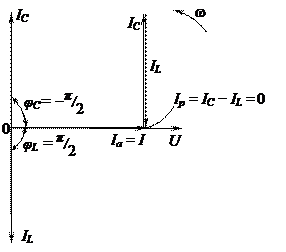
Рис. 28
По аналогии с резонансом напряжений в реактивных элементах токи IL и IC могут значительно превосходить суммарный ток I = Ia, когда будет выполнено условие bL = bC >> g.
|
|
|


