 |
Погрешности измерений: статические и динамические; основные и дополнительные; случайные и систематические. Классы точности средств измерений.
|
|
|
|
Измерение – процесс приема и преобразования информации об измеряемой величине для получения количественного результата, его сравнение с единицей измерения в форме, наиболее удобной для использования. Основная цель измерения – получить максимально приближенный результат к истинному значению измеряемой величины. Степень близости результата измерения к истинному значению называют точностью измерения. Для оценки точности используют понятие погрешность. Погрешность – разность между результатом измерения и истинным значением величины. Классификация погрешностей:
1. по характеру проявления и повторяемости при многократных измерениях погрешности бывают систематическими (остаются неизменными или закономерно изменяются, систематически встречается) и случайными (изменяются случайным образом, не описывается опред.законами и присутствует случайным образом).
2. от характера связи между значением погрешности и уровнем измеряемого сигнала систематические погрешности подразделяются на постоянные – аддитивные (не зависят от уровня сигнала, например-сбой настройки, стрелка отошла на 0,1...) и неаддитивные (зависят от уровня сигнала). При этом характер зависимости неаддитивных погрешностей от уровня сигнала делит их на мультипликативные – прогрессивные (линейная зависимость, увеличиваются или уменьшаются), степенные (резкое возрастание), периодические (гармонический закон-во вращающихся механических элементах) и изменяющиеся по сложному закону.
3. в зависимости от режима работы средства измерения и характера изменения измеряемой величины погрешности бывают статическими (погрешность в статическом режиме (Статический режим определяют как режим, при котором скорость изменения измеряемой (генерируемой) величины значительно меньше (примерно на порядок) скорости собственных движений устройства.), когда измеряемую величину принимают за неизменную) и динамическими (разница между погрешностью измерительного устройства в динамическом режим (динамическим называют режим, при котором скорость изменения измеряемой (генерируемой) величины сравнима со скоростью собственных движений устройства) и его статической погрешностью);
|
|
|
4. в зависимости от условий определения погрешности подразделяют на основные (имеют место при нормальных условиях эксплуатации объекта-20+-5 градусов, 60+-15%, 220+-22В, 50+-5Гц)) и дополнительные (возникают вследствие отклонения каких-либо влияющих величин от нормальных значений, у электронных СИ в зависимости от температуры);
5. в зависимости от представления числового значения: абсолютные (разница между значением измеряемой величины и истинным значением, значение представляется в единицах измеряемой величины, Нормируется при измерении температуры (+-1 градус); относительные (отношение абсолютной погрешности к значению измеряемой величины, определяемые из выражения: 
, где 
- действительное значение измеряемой величины (нужны, чтобы понимать значимость погрешности для диапазона измерения); приведенные (отношение относительной погрешности к нормирующему значению (максимальному из диапазона) определяемые из выражения: 
, где 
- принимаемое по определенным правилам нормирующее значение величины, постоянное во всем диапазоне, Например, для формирования комплекса из различных устройств, но с одинаковой точностью.
Каждый из указанных классов погрешностей имеет свои составляющие. Так например, статическую погрешность составляют: погрешность приближения (погрешность схемы), погрешности от несоответствия размеров и параметров номинальным значениям, производственно-технологические погрешности. А динамические погрешности включают в себя вынужденные (внутренние шумы, наводки) и собственные (их источник: инерционные и демпфирующие элементы).
|
|
|
Для обеспечения единства измерений необходимо знать, с какой точностью измерение выполнено, для этого необходимо нормировать погрешности средств измерения. Поэтому для средств измерений принято деление по точности на классы. Класс точности – обобщенная характеристика средства измерения, определяемая пределами допускаемых погрешностей, а так же другими свойствами средства измерения, влияющими на его точность. Класс точности задают путем нормирования предела допускаемой погрешности. При задании класса точности нормируется предел как абсолютной, так и относительной, так и приведенной погрешностей. Для прибора со шкалами класс точности указывается непосредственно на шкале прибора.
1. Если нормируется предел абсолютной погрешности: 
, то это означает, что нигде в пределах диапазона погрешность средства измерения не превышает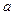 
. При таком нормировании класс точности обозначается римскими цифрами или заглавными буквами латинского алфавита (например, М, С и т.д.). При этом непосредственно из обозначения класса точности невозможно определить чему равняется 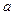(информацию можно узнать в паспорте прибора).
2. Если нормируется предел допускаемой относительной погрешности, то это означает, что нигде в пределах диапазона относительная погрешность не превышает %: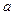 
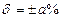. При таком нормировании класс точности обозначается арабскими цифрами из ряда: 1; 1,5; 2; 2,5; 4; 5; 6. Допускается, но не рекомендуется 1,6; 3. Причем цифры могут быть умножены на 10р, где р – целые числа: 1; 0; -1; -2;…На приборе обозначается данная цифра в кружочке. При нормировании относительной погрешности иногда используется другое обозначение: 0,01/0,02. В этом случае предел допускаемой погрешности оказывается зависимым от значения измеряемой величины.
3. Если нормируется приведенная погрешность ( 
.), то класс точности обозначается теми же цифрами, что и в случае относительной погрешности, но только без кружочка.
Обозначения классов точности наносятся на циферблаты, щитки, корпуса средств измерений, приводятся в нормативно-технических документах.
|
|
|
Необходимо еще раз заметить, что класс точности является обобщенной характеристикой средств измерений. Знание его позволяет определить не точность конкретного измерения, а лишь указать пределы, в которых находятся значения измеряемой величины.
Представление результатов измерений. Точечные и интервальные оценки результата измерения: среднеарифметическое значение, среднеквадратическое значение результатов измерений, среднеквадратическое отклонение среднего арифметического, доверительная вероятность, доверительный интервал. Сущность этих оценок, основные формулы для расчета.
Для описания результата измерения наиболее приемлемым подходом является задание закона его вероятности. Однако, определить параметры закона является сложной задачей, поэтому обычно ограничиваются оценками этого закона. Оценки бывают точечные и интервальные.
Рассмотрим точечные оценки. Само название предполагает, что оно определяется одним числом. Пусть имеется n-результатов одной величины
Q: i 
. Предположим, что поправки внесены и, следовательно, закономерно составляющей погрешности нет. Тогда: где Q-истинное значение; 
- значение случайной погрешности; 
следовательно 
.
т.к 
-среднее арифметическое результатов, а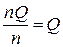 
, то 
а 
Таким образом, средне арифметическое равно истинному, если n= 
, но так как, n 
, то средне арифметическое считается истинным условно.
Точечные оценки:
1. Среднее арифметическое является точечной оценкой истинного значения измеряемой величины и при n 
, точность этой оценки возрастает.
2. Среднеквадратическое отклонение результатов измерений: 
, характеризует степень рассеянности отдельных результатов относительно среднего арифметического. Является мерой случайной погрешности данных измерений.
3. Среднее арифметическое будучи оценкой истинного значения само является величиной случайной. Степень рассеяния среднего арифметического относительно истинного значения характеризует среднеквадратическое отклонение среднего.
|
|
|
Является мерой случайной погрешности многократного измерения.
Результат измерения записывается в виде: 
При возможности переходят к интервальным оценкам.
Интервальные оценки являются более наглядными и удобными для применения. Результат представляется в виде некоторого интервала (доверительного), в пределах которого лежит значение измеряемой величины с определенной доверительной вероятностью.
Доверительный интервал – мера точности результата, чем он шире, тем точность меньше. При нахождении доверительного интервала необходимо знать доверительную вероятность, которая является мерой достоверности и надежности полученного результата.
Чем больше вероятность (больше достоверность полученного результата), тем интервал должен быть шире.
Доверительной вероятностью задаются в зависимости от ответственности этих измерений. Обычно в метрологии 0,9; 0,95, хотя в особо ответственных случаях 0,98; 0,99. Доверительный интервал рассчитывают исходя из полученных точечных оценок и с заданной вероятностью. Обязательным условием нахождения доверительного интервала является знание вида закона распределения вероятности результата.
Здесь имеет место доверительный интервал. Обычно его определяют из выражений: 
-для многократного измерения и 
-для однократного измерения, где 
-квантиль распределения, который определяют исходя из выбранной вероятности и вида закона распределения. Результат измерения записывается в виде 
α - вероятность, n – количество измерений.
В случае нормального закона распределения и числа измерения около25 рекомендуется использовать распределения Стьюдента, если более 25 – критерий Пирсона.
Если закон распределения неизвестен, то в общем случае нельзя рассчитать доверительный интервал.
Очень часто закон распределения результатов измерения является нормальным. Сам по себе нормальный закон имеет место, когда величина зависит от большого числа факторов, среди которых нет доминирующего. Или когда много факторов, а доминирующий распределен по нормальному закону, поэтому прежде всего пытаются проверить является ли закон распределения нормальным.
|
|
|
