 |
Основные составляющие погрешностей измерительных цепей: погрешности приближения.....
|
|
|
|
Точность СИ оценивается величиной погрешности, под которой понимается разность между его индивидуальной и заданной характеристиками (междуд показаниями прибора и значением измеряемой величины): ∆у(х) = уи(х) – у0(х). Погрешность измерит. устр-ва возникает - не удается обеспечить равенство заданной и индивид. хар-к.
Погрешность приближения (погрешность схемы) возникает на этапе структурного синтеза, когда с целью упрощения вместо заданной характеристики реализуется приближенная к ней характеристика. Введение погрешности приближения приводит к упрощению конструкции и технологии изготовления измерительного устройства: повышается точность изготовления и сборки деталей и элементов, а суммарная погрешность оказывается меньше, в связи с упрощением схемы повышается надежность и снижается себестоимость проектируемого устройства. Погрешность приближения - это систематическая погрешность. Примерами приборов с погрешностью приближения нелинейные рычажно-зубчатые индикаторы с равномерной шкалой, электрические приборы для измерения неэлектрических величин, построенные на базе неуравновешенного моста с нелинейной характеристикой, цифровые приборы (дискретизация или квантование сигнала приводят к несоответствию заданной и расчетной характеристик). Определения погрешности приближения:
аналитический метод – погрешность находят как разность м/д номинальной расчетной и заданной хар-ки. 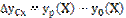
алгоритм: 1) выделяются элементарные преобраз-ные звенья и устанавл-ся связи м/д ними, составляется функц. схема; 2) на основании априорной инф-ции и справочных данных составляются ф-ции преобраз-я элементарных звеньев и записываются ур-я связей; 3) решается с-ма ур-ний, включающая хар-ки элементарных преобраз-х звеньев и ур-я связей, составляется искомая расчетная хар-ка.
|
|
|
экспериментальный метод при испытании опытных образцов: берут N экземпляров однотипных объектов, каждый из к-х п раз поверяют в т точках в пределах всего диапазона. Алгоритм: 1) каждое измерит. устр-во многократно поверяют в выбранных точках и находят средние значения погрешностей в каждой точке; 2) по средним значениям погрешностей определяют в тех же точках средние значения погрешностей для всей группы объектов; 3) экспериментально полученные значения математ. обрабатывают для получения аналитической зависимости ф-ции погрешности схемы на основании ее экспериментального значения.
Погрешности от несоответствия размеров и параметров номинальным – производственно-технологические погрешности, обусловленные проблемами изготовления объекта, реальная характеристик каждого устройства сугубо индивидуальна и всегда отличается от номинальной расчетной. Технологические погрешности носят случайный характер. Источниками технологических погрешностей являются: – несоответствие первичных компонентов и неидентичность техпроцессов при изготовлении материалов для деталей; – несовершенство техпроцессов и оборудования, применяемых при изготовлении деталей и элементов; – несовершенство сборочных, регулировочных и контрольных приспособлений и операций.
Процесс изм-я парам-ра qn хар-ся з-ном распр-я вероят-ти погр-ти f(Δ qn), который оцен-ся мат ожиданием и СКО (М(Δ qn) и S(Δ qn)). При этом в констр-й док-ции задано поле допуска, характер-е нижним EI(Δ qn) и верхним ES(Δ qn) предел-ми отклонениями. На основании инф-ции о поле допуска и др. априорной информации найти мат ожидание и СКО погр-ти для того, чтобы применить рассматриваемый матем-й аппарат для анализа влияющих факторов.К рассмотрению принимаются след-е хар-ки: 1) Середина поля допуска отн-но ном-го значения пар-ра: Е0=(EI+ES)/2.
|
|
|
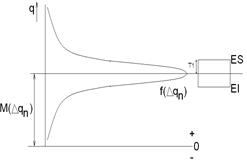 2)Половина поля допуска Т1=(ES-EI)/2 3)Коэффициент относит-й асимметрии, который оценивает величину удаления центра группирования от середины поля допуска:
2)Половина поля допуска Т1=(ES-EI)/2 3)Коэффициент относит-й асимметрии, который оценивает величину удаления центра группирования от середины поля допуска: 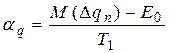 . 4) Коэффициент рассеяния (Относит-е СКО), хар-щий. Какую долю составляет СКО от величины половины поля допуска:
. 4) Коэффициент рассеяния (Относит-е СКО), хар-щий. Какую долю составляет СКО от величины половины поля допуска: 
M(Δqn)=E0 aq=0; 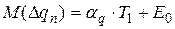 ;
; 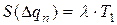
Значения Е0 и Т1 определ-ся из докум-ции, а для нах-я точечных оченок необх-мо знать коэф-т отн-й асимметрии aq и коэф-т рассеяния l, к-рый опр-ся из распр-я самих технологич-х погр-й. Существуют 3 подхода к опр-ю этих хар-к: 1) Определение кривых распр-я по производственнымным наблюдениям путём экспирим-го иссл-я. Применяется в том случае, если рассчитываемый объект уже изг-ся, тогда опр-ся гистограмма по к-рой опр-ся М(Δ qn) и S(Δ qn) по к-рым опр-ся aq и l. 2) Изучение техпроцесса окончат-й обработки. Типовые техпроцессы хар-ся опр-ми видами з-на распр-я погр-й, которые приводятся в соотв-й справочной лит-ре. 3) Выбор кривых распр-я из схематизир-х таблиц. Где указано для разл-х типовых процессов з-ны распр-я и значения aq и l. В этом случае частная погр-ть нах-ся из след-х завис-й:
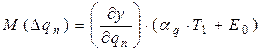 ;
; 
К числу погрешностей от несоответствия параметров номинальным значениям относятся также погрешности из-за износа деталей и старения материалов, а также погрешности от внешних возмущающих воздействий (помех).
Влияющими факторами в последнем случае являются:
– климатические (температура, влажность, давление);
– механические (наклоны, переносные линейные и угловые ускорения, удары, вибрация);
– параметры режимов питания (напряжения, частота, давление, расход);
– параметры внешних полей (магнитных, электрических, радиационных, гравитационных) и т.п. воздействия.
Исключить влияние внешних воздействий невозможно, поэтому погрешность данного типа всегда имеет место. Она является случайной, хотя может иметь существенную систематическую составляющую, например температурная погрешность.
Каждую отдельную неточность внутр. параметра, приводящую к погрешности измерит. цепи, наз. первичной погрешностью (имеет размерность внутр. параметра) у = f(x, q1, q2,…qn); q1→∆q1; q2→∆q2; qn→∆qn – это первичные погрешности. Часть суммарной погрешности проектир. устр-ва, обусловленная первичной погрешностью, называется частной или частичной (имеет размерность выходного сигнала). q1→∆уq1; q2→∆уq2; qn→∆уqn. ∆уq1→∆yΣ; ∆уq2→∆yΣ; ∆уqn →∆yΣ– это суммарные погрешности. Алгоритм опред-я первич. погрешностей:1)Составление перечня первичн. погрешностей,2) Составление описания первичн. погрешностей с учетом их вида (скаляр и вектор, детерминирован и случайн).
|
|
|
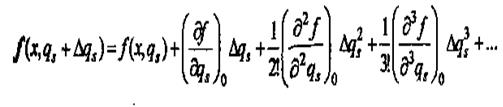
Методы определ-я частных погрешностей.
1 Аналитич. метод для детерминир. скалярных первич. погрешностей. Номин. расчетн. хар-ка: унр=f(x, qn). qn – совок-ть внутр. параметров устр-ва и имеет первичную погрешность ∆qn. В р-те ф-ция преобраз-я: ур=f(x;qn+ ∆qn).Разница между 2мя ф-циями составит частн. погрешность от влияния совокупности внутр. параметров: ∆у∆qn= ур- унр. Пусть ∆qn<<qn, поэтому выражение для расчетной ф-ции можно разложить в ряд Тейлора по степени ∆qn.
Символ ()0 означает, что при взятии частных производных значения всех параметров принимаются без учета первичных погрешностей. Пренебрегая величинами 2го и больших порядков малости, выражение для расчетной ф-ции преобраз-я:
С учетом этого выражение для частной погрешности можно записать в следующем виде:

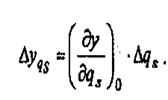
Это выражение наз. осн. формулой линейной теории точности, а значение dy/dqnназ. Коэф-м влияния. Т.о. для нахождения частной погрешности необходимо детерминир. скалярную первичную погрешность умножить на коэф-т влияния. Аналитич. метод опред-я частных погрешностей явл-ся наиболее эффектным, удобным и рекомендуется к применению. Использование не всегда возможно. Ограничение 1: первич погрешность д/б много меньше номинальн. знамения параметра. Ограничение 2: метод не м/б применен в случае нулевых номинальн. значений параметра, поскольку тогда значение параметра отсутствует в расчетной хар-ке, и частную производную взять нельзя. Ограничение 3: при сложных ф-циях преобраз-я м/б затруднительным взятие частных производных. Ограничение 4: метод м/б использован в рассмотренном виде только для независимых первич. погрешностей.
|
|
|
2 Метод преобразованных схем. первич. погрешность моделируют с помощью дополнит. генераторов в электрич. цепи. При этом искомое значение частной погрешности определяют как ф-цию вых. сигнала при неизменном вх. сигнале и при применении моделирования к первичной погрешности.
3 Геометрический метод применяется при расчете точности механизмов, при этом механизм строят в 2х положениях, наложенных одно на другое. Одно из них без погрешности, другое – с погрешностью. Искомое значение погрешности определяют из геометрических соотношений, используя для этого правила и законы геометрии.
Погрешности от действия внутренних дестабилизирующих факторов (материально-структурные погрешности) возникают под влиянием дополнит. (вредных) возд-й, не предусмотренных принципом действия прибора. Для механизмов приборов это, прежде всего, силовые погрешности: - силы и моменты трения в опорах, направляющих и шарнирных соединениях; - силы и моменты от неуравновешенности подвижной системы; - силы и моменты от взаимодействия подвижной системы с внутренними магнитными и электрическими полями; - аэродинамические, гидродинамические силы и моменты, возникающие при обтекании подвижной системы воздушными или газовыми потоками; - гидростатические силы (при расположении подвижной системы жидкости) и т.п. Для электронных и электромеханических цепей источниками таких воздействий являются: - паразитные термо-ЭДС в соединениях разнородных проводников; - сопротивления утечек; - паразитные индуктивные и емкостные связи;
- внутренние шумы радиоэлектронных элементов и т.п. Погрешности рассматриваемого типа носят случайный характер.
Механизм влияния указанных факторов на погрешность проектируемого устройства заключается, как правило, в их воздействии на значения внутренних параметров. Так, например, повышение температуры вызывает изменение линейных размеров деталей, упругих свойств материалов, электрического сопротивления проводников и т.п., что в свою очередь приводит к изменению функции преобразования измерительного устройства и к появлению указанной составляющей погрешности. Если влияющие факторы изменяются в пределах, оговоренных нормальными условиями, то учет этих факторов производится на этапе расчета основной погрешности. Если изменения выходят за указанные пределы, то их учитывают при определении дополнительных погрешностей.
36 Погрешность приближения измерительных цепей......
Точность СИ оценивается величиной погрешности, под к-й понимается разность м/д его индивидуальной и заданной хар-ми (между показаниями прибора и значением измеряемой величины): ∆у(х) = уи(х) – у0(х). Погрешность измерит. устр-ва возникает вследствие того, что не удается обеспечить равенство заданной хар-ки и хар-ки индивидуальной. Т.о. погрешность измерит. устр-ва может возникать на различных этапах его жизненного цикла, при этом на этапе проектирования необходимо уметь выявлять и оценивать отдельные составляющие погрешности, а также определять полную погрешность при проведении анализа точности.
|
|
|
Погрешность приближения (погрешность схемы) ОНА СИСТЕМАТИЧЕСКАЯ ИНСТРУМЕНТАЛЬНАЯ когда невозможно или нецелесообразно точно реализовать заданную характеристику. Чаще всего эта проблема возникает, когда требуемая линейная характеристика реализуется звеньями с нелинейными функциями преобразования. Введение погрешности приближения приводит к упрощению конструкции и технологии изготовления измерит. устр-ва, повышается точность изготовления и сборки деталей и элементов, а суммарная погрешность оказывается меньше, чем у объекта с точной, но сложной схемой, в связи с упрощением схемы повышается надежность и снижается себестоимость проектируемого устройства. Погрешность приближения - это систематическая погрешность. Приборы с погрешностью приближения можно считать нелинейные рычажно-зубчатые индикаторы с равномерной шкалой (рычаг в виде синусного или тангенсного механизмов имеет нелинейную характеристику), электрические приборы для измерения неэлектрических величин, построенные на базе неуравновешенного моста с нелинейной характеристикой, цифровые приборы (дискретизация или квантование сигнала приводят к несоответствию заданной и расчетной характеристик).
Для определения погрешности приближения - аналитический метод, согласно которому погрешность находят как разность между номинальной расчетной и заданной хар-ми.
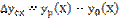
Алгоритм: 1) выделяются элементарные преобразовательные звенья и устанавливаются связи между ними, т.е. составляется его функциональная схема; 2) на основании априорной инф-ции и справочных данных составляются ф-ии преобразования элементарных звеньев и записываются ур-ния связей; 3) решается система ур-ний, включающая хар-ки элементарных преобразоват. звеньев и ур-ния связей, составляется искомая расчетная хар-ка. При испытании опытных образцов применяют экспериментальный метод. берут N экземпляров однотипных объектов, каждый из которых п раз поверяют в т точках в пределах всего диапазона. Алгоритм: 1) каждое измерит. устр-во многократно поверяют в выбранных точках и находят средние значения погрешностей в каждой точке; 2) по средним значениям погрешностей определяют в тех же точках средние значения погрешностей для всей группы объектов; 3) экспериментально полученные значения математ. обрабатывают для получения аналитической зависимости ф-ции погрешности схемы на основании ее экспериментального значения. Пути снижения влияния погрешности приближения на точность измерительного устройства Погрешность приближения – это ф-ция, к-я дает различные значения погрешности в пределах всего диапазона преобразования. При нормировании точности во внимание принимается max значение погрешности. Поэтому под критерием минимума погрешности приближения: max значение этой погрешности в пределах всего диапазона принимает min возможное значение. Погрешность приближения является систематической. методов снижения влияния: - регулирование объекта; - проведение параметрического синтеза по критерию минимума погрешности приближения; - введение в схему средства измерения корректирующих звеньев (компенсаторов); - построение шкалы отсчетного устр-ва в соответствии с расчетной хар-кой (неравномерная шкала); - внесение поправок в показания или ф-цию преобразования объекта. Регулирование путем изменения отдельных параметров добиваются уменьшения max в пределах диапазона значения погрешности приближения. два вида регулировки: Регулировка рабочего участка направлена на совмещение диапазона преобразования проектируемого устр-ва с участком его хар-ки, наилучшим образом соответствующим заданной хар-ке, в частности, обладающим наибольшей линейностью при нелинейной расчетной функции преобразования. Регулировка чувствительности ставит задачу путем изменения соответствующих параметров цепи получить в заранее выбранных точках значение погрешности, равное нулю. При регулировании осуществляют калибровку средства измерения в выбранных точках и изменение параметров до получения нулевых значений погрешности.
Параметрический синтез по критерию минимума погрешности приближения. Регулирование объекта показывает, что изменяя внутренние параметры устройства можно выбрать такие их значения, при которых погрешность схемы будет минимальной. Математически можно поставить следующую задачу: определить параметры q1, q2,…qn из условия минимума максимальной погрешности приближения ∆усх(х, q1, q2,… qn). При этом погрешность схемы ∆усх рассматривается как ф-ция в заданном диапазоне входного воздействия х, х Є [а;b], где а и b – пределы преобразования. Существует 2 подхода. 1) Последовательное рассмотрение всех возможных комбинаций значения внутренних параметров с расчетом для каждой комбинации максимального значения ∆усх и выбора той комбинации, где ∆усх будет минимальной. 2) Аналитическое определение оптимальных параметров устройства с использованием полиномов Чебышева.(Задача синтеза по критерию минимума погрешности приближения сводится к расчету значений внутренних параметров, при кот. функция 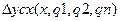 с заданной степенью точности, совпадает с функцией Pn(x) или Rn(x). Обычно ипользуют полином Чебышева не выше 4..5 порядка).Алгоритм синтеза: 1) Составление мат.описания объекта проетирования и получения аналитического выражения для погрешности схемы, 2) Определение дополнительного значения погрешности приближения, 3) Выбор вида полинома Чебышева, 4) Определение наименьшей степени полинома, 5) Проведение замены переменных, 6) Определение опытных значений параметров. 7) Определение максимального значения погрешности приближения. 8) Проверка эффективности синтеза, 9) Сравнение ∆усхmax с допустимым значением. Обычно параметрический синтез и регулировка обеспечивают пренебрежимо малые значения погрешности приближения. Если этого добиться не удается и погрешность приближения остается существенной, то применяют другие методы.
с заданной степенью точности, совпадает с функцией Pn(x) или Rn(x). Обычно ипользуют полином Чебышева не выше 4..5 порядка).Алгоритм синтеза: 1) Составление мат.описания объекта проетирования и получения аналитического выражения для погрешности схемы, 2) Определение дополнительного значения погрешности приближения, 3) Выбор вида полинома Чебышева, 4) Определение наименьшей степени полинома, 5) Проведение замены переменных, 6) Определение опытных значений параметров. 7) Определение максимального значения погрешности приближения. 8) Проверка эффективности синтеза, 9) Сравнение ∆усхmax с допустимым значением. Обычно параметрический синтез и регулировка обеспечивают пренебрежимо малые значения погрешности приближения. Если этого добиться не удается и погрешность приближения остается существенной, то применяют другие методы.
|
|
|


