Погрешности от несоответствия действительных значений внутренних параметров номинальным значениям: определение, причины возникновения, характеристики, методы расчета.

Погрешности от несоответствия размеров и параметров номинальным – производственно-технологические погрешности, обусловленные проблемами изготовления объекта, реальная хар-ка каждого устр-ва сугубо индивидуальна и всегда отличается от номинальной расчетной.

Делится на: 1) Производственно технологическая погрешность – обусловлена невозможностью идиально точного изготовления объекта в следствии чего на этапе параметрического синтеза задаются поля допусков на все параметры и размеры, а в результате каждый экземпляр устройства имеет присущие только ему сочитание действительных значений этих размеров и параметров, т.е. всегда присутсвует технологическая погрешность. Технологич. погрешности носят случайный хар-р.

Источниками технологических погрешностей являются:

– несоответствие первичных компонентов и неидентичность технологических процессов при изготовлении материалов для деталей, что приводит к разбросу физических параметров (плотности, модуля упругости, удельного электрического сопротивления, магнитной проницаемости и т.п.);

– несовершенство технологических процессов и оборудования, применяемых при изготовлении деталей и элементов, включая термическую, гальваническую, магнитную и электрическую обработку, что вызывает рассеяние геометрических размеров и параметров деталей и элементов;

– несовершенство сборочных, регулировочных и контрольных приспособлений и операций, что приводит к погрешностям узлов и блоков при их сборке и регулировке.

Каждая отдельная неточность внутреннего параметра приводящего к погрешности измерительной цепи называют ПЕРВИЧНОЙ ПОГРЕШНОСТЬЮ! Так же первичная погрешность–погрешность параметров входящих в функцию преобразования кроме этого к числу первичных погрешностей могут относится отклонения от правельной геометрической формызазоры в подвижных соединениях и т.д. Имеет размерность внутреннего параметра. Часть суммарной погрешности проектируемого устройства обусловленная первияной погрешностью, называется частной погрешностью(размерность вых. величины). Т.о составляют перечень первичных погрешностей, затем производится анализ вида погрешностей!

Первичные погрешности делятся на:

– Скалярные(погрешность кот. характеризутся только значением с учетом знака (погрешность сопративления, длинны))

– Векторные (погрешность, кот. характеризуется нетолько значением, но и направлением действия(экстраситет?????забыл как правельно))

– Детерменированные (погрешноти, кот. изменяются по определённым заранее известным законам)

– Случайные (погрешности, принимающие случайные значения)

Мат описание Детерменированная сколярная погрешность Δq_n=а

Мат описание случайной сколярной погрешности описывается законом распределения кот. представляется основными моментами мат ожидания М(Δq_n) и СКО S(Δq_n)

Векторная детерменированная погрешность описывается |Δq_n|=а, φ _Δqn=b

Векторная случайная погрешность для неё надо задать виды законов распределения вероятности модуля(значения) и аргумента(направление действия) с указанием соответствующих точечных оценок М(Δq_n) и СКО S(Δq_n), М(φ _Δqn) и S(φ _Δqn)

Методы определения:

1 Аналитич. метод для детерминир. скалярных первич. погрешностей. Номин. расчетн. хар-ка: у_нр=f(x, q_n). q_n – совок-ть внутр. параметров устр-ва и имеет первичную погрешность ∆q_n. В р-те ф-ция преобраз-я: у_р=f(x;q_n+ ∆q_n).Разница между 2мя ф-циями составит частн. погрешность от влияния совокупности внутр. параметров: ∆у_∆qn= у_р- у_нр. Пусть ∆q_n<<q_n, поэтому выражение для расчетной ф-ции можно разложить в ряд Тейлора по степени ∆q_n.

Символ ()₀ означает, что при взятии частных производных значения всех параметров принимаются без учета первичных погрешностей. Пренебрегая величинами 2го и больших порядков малости, выражение для расчетной ф-ции преобраз-я:

С учетом этого выражение для частной погрешности можно записать в следующем виде:

Это выражение наз. осн. формулой линейной теории точности, а значение dy/dq_nназ. Коэф-м влияния. Т.о. для нахождения частной погрешности необходимо детерминир. скалярную первичную погрешность умножить на коэф-т влияния. Аналитич. метод опред-я частных погрешностей явл-ся наиболее эффектным, удобным и рекомендуется к применению. Использование не всегда возможно. Ограничение 1: первич погрешность д/б много меньше номинальн. знамения параметра. Ограничение 2: метод не м/б применен в случае нулевых номинальн. значений параметра, поскольку тогда значение параметра отсутствует в расчетной хар-ке, и частную производную взять нельзя. Ограничение 3: при сложных ф-циях преобраз-я м/б затруднительным взятие частных производных. Ограничение 4: метод м/б использован в рассмотренном виде только для независимых первич. погрешностей.

2 Метод преобразованных схем. первич. погрешность моделируют с помощью дополнит. генераторов в электрич. цепи. При этом искомое значение частной погрешности определяют как ф-цию вых. сигнала при неизменном вх. сигнале и при применении моделирования к первичной погрешности.

Алгоритм для механизмов:

1) Замена исследуемого звена q_n на группу звеньев, так, чтобы погрешность Δq_n можно было бы изменять, 2)Закрепление ведущего звена в одном заданном положении, 3) построение в масштабе плана малых перемещений для преобразованного механизма, 4) Определение по плану значения частной погрешности Δyq_n

Алгоритм для Эл.цепей:

1) Представление Эл.цепи в виде блока с напрядением (Е) на вх. и напряжением (U) на выходе и выделение из блока исследуемого элемента(сопративление R с погрешностью ΔR),

 

 

2) Определение влияния этой погрешности на выходное напряжение в соответствии с линейной теорий точности.

ΔU=Е(, f- функция параметров Эл.цепи, 3) Преобразуют схему для того чтобы решить проблему заключающаяся в определении коэффициента влияния первичной погрешности. Преобразование схемы проводят таким образом, чтобы можно было смоделировать первичную погрешность ΔR с помомощью доп. Генератора с ЕДС.

Uг=μ* Δе, Δе- падение напряжения на участке вкл.генератора, μ-масштабный коэффициент, с кот передается действительное падение U вызванное увеличением сопративлением R на ΔR: Δе=-(i+ Δi)* ΔR=-i* ΔR следует Uг=-μ*i* ΔR

Знак -, означает что дополнительный источник питания создает на участве включения ток (i) противоположенный основному току. 4) Закорачивание полюсов на входе цепи и вкл доп генератора приводит к тому, что на входе схемы возникает напряжение(U’) U’=μ* ΔU, μ=U’/ ΔU, тогда Uг=-(U’/ ΔU)*i* ΔR. 5) Определение частной погрешности ведется при приравнивании ΔU=-(U’/ Uг)*i* ΔR(преобраз схема) и ΔU=Е(,(исходная схема) погрешность будет равна

ΔU=-(U’/ Uг)*i* ΔR

3 Геометрический метод применяется при расчете точности механизмов, при этом механизм строят в 2х положениях, наложенных одно на другое. Одно из них без погрешности, другое – с погрешностью. Искомое значение погрешности определяют из геометрических соотношений, используя для этого правила и законы геометрии.

Процесс изм-я парам-ра q_n хар-ся з-ном распр-я вероят-ти погр-ти f(Δ q_n), который оцен-ся мат ожиданием и СКО (М(Δ q_n) и S(Δ q_n)). При этом в констр-й док-ции задано поле допуска, характер-е нижним EI(Δ q_n) и верхним ES(Δ q_n) предел-ми отклонениями. На основании инф-ции о поле допуска и др. априорной инф-ции найти мат ожидание и СКО погр-ти для того, чтобы применить рассматриваемый матем-й аппарат для анализа влияющих факторов.К рассмотрению принимаются след-е хар-ки: 1) Середина поля допуска отн-но ном-го значения пар-ра: Е₀=(EI+ES)/2.

2)Половина поля допуска Т₁=(ES-EI)/2 3)Коэффициент относит-й асимметрии, который оценивает величину удаления центра группирования от середины поля допуска: 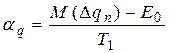. M(Δq_n)=E₀ a_q=0 4) Коэффициент рассеяния (Относит-е СКО), хар-щий. Какую долю составляет СКО от величины половины поля допуска:

;

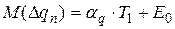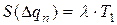
Значения Е₀ и Т₁ определ-ся из докум-ции, а для нах-я точечных оченок необх-мо знать коэф-т отн-й асимметрии a_q и коэф-т рассеяния l, к-рый опр-ся из распр-я самих технологич-х погр-й. Существуют 3 подхода к опр-ю этих хар-к: 1) Определение кривых распр-я по производственнымным наблюдениям путём экспирим-го иссл-я. Применяется в том случае, если рассчитываемый объект уже изг-ся, тогда опр-ся гистограмма по к-рой опр-ся М(Δ q_n) и S(Δ q_n) по к-рым опр-ся a_q и l. 2) Изучение техпроцесса окончат-й обработки. Типовые техпроцессы хар-ся опр-ми видами з-на распр-я погр-й, которые приводятся в соотв-й справочной лит-ре. 3) Выбор кривых распр-я из схематизир-х таблиц. Где указано для разл-х типовых процессов з-ны распр-я и значения a_q и l. В этом случае частная погр-ть нах-ся из след-х завис-й:

;

К числу погрешностей от несоответствия параметров номинальным значениям относятся также2) погрешности из-за износа деталей и старения материалов, а также 3) погрешности от внешних возмущающих воздействий (помех).

Влияющими факторами в последнем случае являются:

– климатические (температура, влажность, давление);

– механические (наклоны, переносные линейные и угловые ускорения, удары, вибрация);

– параметры режимов питания (напряжения, частота, давление, расход);

– параметры внешних полей (магнитных, электрических, радиационных, гравитационных) и т.п. воздействия.

Исключить влияние внешних воздействий невозможно, поэтому погрешность данного типа всегда имеет место. Она является случайной, хотя может иметь существенную систематическую составляющую, например температурная погрешность.

Механизм влияния указанных факторов на погрешность проектируемого устройства заключается, как правило, в их воздействии на значения внутренних параметров. Так, например, повышение температуры вызывает изменение линейных размеров деталей, упругих свойств материалов, электрического сопротивления проводников и т.п., что в свою очередь приводит к изменению функции преобразования измерительного устройства и к появлению указанной составляющей погрешности. Если влияющие факторы изменяются в пределах, оговоренных нормальными условиями, то учет этих факторов производится на этапе расчета основной погрешности. Если изменения выходят за указанные пределы, то их учитывают при определении дополнительных погрешностей.

При анализе точности измерительных устройств, основанных на косвенных методах измерения, выделяется погрешность метода, возникающая каждый раз, когда параметры l_i (i =1, 2, ..., n), входящие в уравнение метода измерения:

x = f (l_i, x*),

где x – подлежащая измерению величина;

x* – величина, на которую реагирует чувствительный элемент,

не остаются постоянными. В качестве примера такой погрешности можно привести погрешность термоэлектрического термометра вследствие вариации температуры холодного спая.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: