Глава: Кодирование в системах ПДС.

 

П. 3.1 Классификация кодов:

Известно большое число помехоустойчивых кодов, которые классифицируются по различным признакам. Помехоустойчивые коды можно разделить на два больших класса: блочные и непрерывные. При блочном кодировании последовательность элементарных сообщений источника разбивается на отрезки и каждому отрезку ставится в соответствие определенная последовательность (блок) кодовых символов, называемая обычно кодовой комбинацией. Множество всех кодовых комбинаций, возможных при данном способе блочного кодирования, и есть блочный код.

Длина блока может быть как постоянной, так и переменной. Различают равномерные и неравномерные блочные коды. Помехоустойчивые коды являются, как правило, равномерными.

Блочные коды бывают разделимыми и неразделимыми. К разделимым относятся коды, в которых символы по их назначению могут быть разделены на информационные символы, несущие информацию о сообщениях и проверочные. Такие коды обозначаются как (n, k), где n - длина кода, k - число информационных символов. Число комбинаций в коде не превышает 2 ^k. К неразделимым относятся коды, символы которых нельзя разделить по их назначению на информационные и проверочные.

Коды с постоянным весом характеризуются тем, что их кодовые комбинации содержат одинаковое число единиц: Примером такого кода является код “3 из 7”, в котором каждая кодовая комбинация содержит три единицы и четыре нуля (стандартных телеграфный код № 3).

Коды с постоянным весом позволяют обнаружить все ошибки кратности q=1,...,n за исключением случаев, когда число единиц, перешедших в нули, равно числу нулей, перешедших в единицы. В полностью асимметричных каналах, в которых имеет место только один вид ошибок (преобразование нулей в единицы или единиц в нули), такой код дозволяет обнаружить все ошибки. В симметричных каналах вероятность необнаруженной ошибки можно определить как вероятность одновременного искажения одной единицы и одного нуля:

где Pош вероятность искажения символа.

Среди разделимых кодов различают линейные и нелинейные. К линейным относятся коды, в которых поразрядная сумма по модулю 2 любых двух кодовых слов также является кодовым словом. Линейный код называется систематическим, если первые k символов его любой кодовой комбинации являются информационными, остальные (n- k) символов — проверочными.

Среди линейных систематических кодов наиболее простой код (n, n-k), содержащий один проверочный символ, который равен сумме по модулю 2 всех информационных символов. Этот код, называемый кодом с проверкой на четность, позволяет обнаружить все сочетания ошибок нечетной кратности. Вероятность необнаруженной ошибки в первом приближении можно определить как вероятность искажения двух символов:

Подклассом линейных кодов являются циклические коды. Они характеризуются тем, что все наборы, образованные циклической перестановкой любой кодовой комбинации, являются также кодовыми комбинациями. Это свойство позволяет в значительной степени упростить кодирующее и декодирующее устройства, особенно при обнаружении ошибок и исправлении одиночной ошибки. Примерами циклических кодов являются коды Хэмминга, коды Боуза - Чоудхури - Хоквингема (БЧХ — коды) и др.

Примером нелинейного кода является код Бергера, у которого проверочные символы представляют двоичную запись числа единиц в последовательности информационных символов. Например, таким является код: 00000; 00101; 01001; 01110; 10001; 10110; 11010; 11111. Коды Бергера применяются в асимметричных каналах. В симметричных каналах они обнаруживают все одиночные ошибки и некоторую часть многократных.

Непрерывные коды характеризуются тем, что операции кодирования и декодирования производятся над непрерывной последовательностью символов без разбиения ее на блоки. Среди непрерывных, наиболее применимы сверточные коды.

Как известно, различают каналы с независимыми и группирующимися ошибками. Соответственно помехоустойчивые коды можно разбить на два класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Далее будут рассматриваться в основном коды, исправляющие независимые ошибки. Это объясняется тем, что хотя для исправления пакетов ошибок разработано много эффективных кодов, на практике целесообразнее использовать коды, исправляющие независимые ошибки вместе с устройством перемежения символов или декорреляции ошибок. При этом символы кодовой комбинации не передаются друг за другом, перемешиваются с символами других кодовых комбинаций. Если интервал между символами, принадлежащими одной кодовой комбинации, сделать больше чем “память” канала, то ошибки в пределах кодовой комбинации можно считать независимыми, что и позволяет использовать коды, исправляющие независимые ошибки.

Эффективное кодирование — это процедура, направленная на устранение избыточности. К нему относится метод Хаффмана. Трек - ситуация, когда 1я ошибка в одной комбинации приводит к неверному декодированию нескольких подряд идущих символов (возникновение трека случайно).

Арифметическое кодирование - метод, позволяющий упаковывать символы входного алфавита без потерь. При том условии, что известно распределение частот этих символов и является наиболее оптимальным, т к достигается теоретическая граница степени сжатия.

Корректирующие коды. Делятся на блочные и непрерывные. К блочным относятся коды, в которых каждому символу алфавита соответствует блок (кодовая комбинация) из п (i) элементов, где i - номер сообщения. Если п (i) = п, т е длина блока постоянна и не зависит от номера сообщения, то код называется равномерным. Такие коды чаще применяются на практике. Если длина блока зависит от номера сообщения, то такой код - неравномерный. В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы размещаются в определенном порядке между информационными. Корректирующие коды позволяют обнаруживать или исправлять ошибки.

Расстояние Хемминга (для любых двух кодовых комбинаций определяется числом несовпадающих в них разрядов) также используется в корректирующих кодах. Кодовое расстояние - минимальное расстояние Хемминга между всеми парами разрешенных комбинаций. Код Хемминга - код с расстояниями 3 и 4.

Циклические коды. Данное название происходит от основного свойства этих кодов: если некоторая кодовая комбинация a₁, а₂,......, a_n-1, a_n принадлежит циклическому коду, то комбинации a_n, a₁, а₂,........, a_n-1; a_n-1, a_n, a₁, а₂,. ......, а_n-2 и т.д., полученные циклической перестановкой элементов, также принадлежат этому коду. Вторым свойством всех разрешенных кодовых комбинаций ци­клических кодов (как полиномов) является их делимость без остатка на некоторый выбранный полином, называемый производящим.

Итеративный код - комбинация двух линейных кодов. Такие коды борются с группирующимися ошибками.

Каскадные коды - исходная информация последовательно разбивается на сегменты двоичных элементов. Каждый сегмент является единичным элементом недвоичного кода. По правилам недвоичного кода к информационным добавляются недвоичные проверочные элементы. Любое количество ошибок в пределах недвоичного элемента считается однократной ошибкой. Каждый недвоичный элемент защищается недвоичным корректирующим кодом.

Эффективное кодирование

Эффективное кодирование – это процедуры направленные на устранение избыточности.
Основная задача эффективного кодирования – обеспечить, в среднем, минимальное число двоичных элементов на передачу сообщения источника. В этом случае, при заданной скорости модуляции обеспечивается передача максимального числа сообщений, а значит максимальная скорости передачи информации.

Пусть имеется источник дискретных сообщений, алфавит которого .
При кодировании сообщений данного источника двоичным, равномерным кодом, потребуется двоичных элементов на кодирование каждого сообщения.

Если вероятности появления всех сообщений источника равны, то энтропия источника (или среднее количество информации в одном сообщении) максимальна и равна .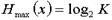

В данном случае каждое сообщение источника имеет информационную емкость 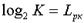бит, и очевидно, что для его кодирования (перевозки) требуется двоичная комбинация не менее 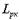элементов. Каждый двоичный элемент, в этом случае, будет переносить 1 бит информации.

Если при том же объеме алфавита сообщения не равновероятны, то, как известно, энтропия источника будет меньше

.

Если и в этом случае использовать для перевозки сообщения 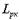-разрядные кодовые комбинации, то на каждый двоичный элемент кодовой комбинации будет приходиться меньше чем 1 бит.

Появляется избыточность, которая может быть определена по следующей формуле

.

Среднее количество информации, приходящееся на один двоичный элемент комбинации при кодировании равномерным кодом

Пример: Для кодирования 32 букв русского алфавита, при условии равновероятности, нужна 5 разрядная кодовая комбинация. При учете ВСЕХ статистических связей реальная энтропия составляет около 1,5 бит на букву. Нетрудно показать, что избыточность в данном случае составит

,

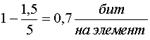Если средняя загрузка единичного элемента так мала, встает вопрос, нельзя ли уменьшить среднее количество элементов необходимых для переноса одного сообщения и как наиболее эффективно это сделать?

Для решения этой задачи используются неравномерные коды.

При этом, для передачи сообщения, содержащего большее количество информации, выбирают более длинную кодовую комбинацию, а для передачи сообщения с малым объемом информации используют короткие кодовые комбинации.

Учитывая, что объем информации, содержащейся в сообщении, определяется вероятностью появления

, можно перефразировать данное высказывание.

Для сообщения, имеющего высокую вероятность появления, выбирается более короткая комбинация и наоборот, редко встречающееся сообщение кодируется длинной комбинацией.

Т.о. на одно сообщение будет затрачено в среднем меньшее единичных элементов 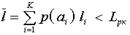, чем при равномерном.

Если скорость телеграфирования постоянна, то на передачу одного сообщения будет затрачено в среднем меньше времени

А значит, при той же скорости телеграфирования будет передаваться большее число сообщений в единицу времени, чем при равномерном кодировании, т.е. обеспечивается большая скорость передачи информации.

Каково же в среднем минимальное количество единичных элементов требуется для передачи сообщений данного источника? Ответ на этот вопрос дал Шеннон.

 

Шеннон показал, что

1. Нельзя закодировать сообщение двоичным кодом так, что бы средняя длина кодового слова была численно меньше величины энтропии источника сообщений. , где

2. Существует способ кодирования, при котором средняя длина кодового слова немногим отличается от энтропии источника

Остается выбрать подходящий способ кодирования.

Эффективность применения оптимальных неравномерных кодов может быть оценена:

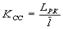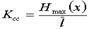1. Коэффициентом статистического сжатия, который характеризует уменьшение числа двоичных элементов на сообщение, при применении методов эффективного кодирования в сравнении с равномерным . Учитывая, что , можно записать . Ксс лежит в пределах от 1 - при равномерном коде до , при наилучшем способе кодирования.

2. Коэффициент относительной эффективности

- позволяет сравнить эффективность применения различных методов эффективного кодирования.

В неравномерных кодах возникает проблема разделения кодовых комбинаций. Решение данной проблемы обеспечивается применением префиксных кодов.

Префиксным называют код, для которого никакое более короткое слово не является началом другого более длинного слова кода. Префиксные коды всегда однозначно декодируемы.

Введем понятие кодового дерева для множества кодовых слов.

 

Наглядное графическое изображение множества кодовых слов можно получить, установив соответствие между сообщениями и концевыми узлами двоичного дерева. Пример двоичного кодового дерева изображен на рисунке 12.

Рис.12. Пример двоичного кодового дерева

 

Две ветви, идущие от корня дерева к узлам первого порядка, соответствуют выбору между “0” и “1” в качестве первого символа кодового слова: левая ветвь соответствует “0”, а правая – “1”. Две ветви, идущие из узлов первого порядка, соответствуют второму символу кодовых слов, левая означает “0”, а правая – “1” и т. д. Ясно, что последовательность символов каждого кодового слова определяет необходимые правила продвижения от корня дерева до концевого узла, соответствующего рассматриваемому сообщению.

Формально кодовые слова могут быть приписаны также промежуточным узлам. Например, промежуточному узлу второго порядка на рис.1 можно приписать кодовое слово 11, которое соответствует первым двум символам кодовых слов, соответствующих концевым узлам, порождаемых этим узлом. Однако кодовые слова, соответствующие промежуточным узлам, не могут быть использованы для представления сообщений, так как в этом случае нарушается требование префиксности кода.

Требование, чтобы только концевые узлы сопоставлялись сообщениям, эквивалентно условию, чтобы ни одно из кодовых слов не совпало с началом (префиксом) более длинного кодового слова.

Любой код, кодовые слова которого соответствуют различным концевым вершинам некоторого двоичного кодового дерева, является префиксным, т. е. однозначно декодируемым.

Метод Хаффмена

Одним из часто используемых методов эффективного кодирования является так называемый код Хаффмена.

Пусть сообщения входного алфавита имеют соответственно вероятности их появления .

Тогда алгоритм кодирования Хаффмена состоит в следующем:

1. Сообщения располагаются в столбец в порядке убывания вероятности их появления.

2. Два самых маловероятных сообщения объединяем в одно сообщение , которое имеет вероятность, равную сумме вероятностей сообщений , т. е. . В результате получим сообщения , вероятности которых .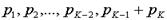

3. Повторяем шаги 1 и 2 до тех пор, пока не получим единственное сообщение, вероятность которого равна 1.

4. Проводя линии, объединяющие сообщения и образующие последовательные подмножества, получаем дерево, в котором отдельные сообщения являются концевыми узлами. Соответствующие им кодовые слова можно определить, приписывая правым ветвям объединения символ “1”, а левым - “0”. Впрочем, понятия “правые” и “левые” ветви в данном случае относительны.

На основании полученной таблицы можно построить кодовое дерево

Так как в процессе кодирования сообщениям сопоставляются только концевые узлы, полученный код является префиксным и всегда однозначно декодируем.

При равномерных кодах одиночная ошибка в кодовой комбинации приводит к неправильному декодированию только этой комбинации. Одним из серьёзных недостатков префиксных кодов является появление трека ошибок, т.е. одиночная ошибка в кодовой комбинации, при определенных обстоятельствах, способна привести к неправильному декодированию не только данной, но и нескольких последующих кодовых комбинаций.

Метод Хаффмана обладает некоторыми недостатками:

1)сложно реализуется адаптация

2)длины кодовых комбинаций выражаются только целыми числами, минимальная длина – один элемент.

Арифметическое кодирование

Арифметическое кодирование является методом, позволяющим упаковывать символы входного алфавита без потерь при условии, что известно распределение частот этих символов и является наиболее оптимальным, т.к. достигается теоретическая граница степени сжатия

Достоинства:

1) Способность кодирования символа с количеством битв сколь угодно близким к предельному

2) возможность адаптивного изменения модели

3) высокая скорость работы

Пусть имеется алфавит из 3 сообщений:

а₁ → Р(а₁)=0,5; а₂ → Р(а₂)=0,2; а₃ → Р(а₃)=0,3. .

Допустим, кодируемый блок а₁ а₃ а₂ (рис. 13)

Разбиваем единичный отрезок на отрезки, равные сообщениям.

Шаг 1

Выбираем участок, соответствующий первому сообщению в кодируемом блоке. Разбиваем его пропорционально суммарным вероятностям. Находим нижние и верхние границы сообщений.

В общем виде:

нижняя граница ,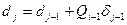

где j – номер сообщение в кодируемом блоке,

i – номер сообщение в исходном алфавите,

δ – ширина предыдущего участка;

верхняя граница ,

ширина участка .

Шаг 2

Выбираем участок, соответствующий а₃. Разбиваем его пропорционально.

Кодируем а_2. Находим нижнюю и верхнюю границы, ширину а_2.

Получаем число-архив: .

Количество разрядов, необходимое для представления архива в двоичном виде определяется как .

Т.о., чем меньше ширина участка, т.е. чем меньше вероятность сообщения, тем больше количество двоичных разрядов потребуется для представления числа-архива в двоичном виде.

Графически метод арифметического кодирования представлен на рисунке 13.

 

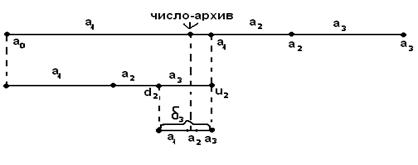
Рис.13.

Недостатки метода Хаффмана:

1. Сложно реализуется адаптация;

2. Длины кодовых комбинаций выражаются только целыми числами (минимальная длина – 1 элемент).

Плюсы арифметического кодирования:

1.Способность кодирования символа с количеством бит, сколь угодно близко предельной.

2. Возможность адаптивного изменения модели или вероятностей.

3. Высокая скорость работы.

Циклические коды

 

Широкое распространение получил класс линейных кодов, которые называются циклическими. Название этих кодов происходит от их основного свойства: если кодовая комбинация a₁, а₂,......, a_n-1, a_n принадлежит циклическому коду, то комбинации a_n, a₁, а₂,........, a_n-1; a_n-1, a_n, a₁, а₂,. ......, а_n-2 и т.д., полученные циклической перестановкой элементов, также принадлежат этому коду.

Общим свойством всех разрешенных кодовых комбинаций циклических кодов (как полиномов) является их делимость без остатка на некоторый выбранный полином, называемый производящим. Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на этот полином. Описание циклических кодов и их построение обычно проводят с помощью многочленов (полиномов). Цифры двоичного кода можно рассматривать как коэффициенты многочлена переменной х.

Поскольку любое число в произвольной системе счисления можно записать в виде a_n-1×х^n-1+a_n-2×x^n-2+...+ а₀×х⁰, где х-основание системы счисления, a_n-1,...,a₀ – цифры этой системы, то переход от двоичного числа к записи в виде многочлена осуществляется следующим образом:

11011® 1×x⁴ + 1×х³ +0×х²+1×x¹ +1×x⁰=x⁴+x³+x+1

Отсюда видно, что кодовая комбинация длиной п (п=5) описывается многочленом степени п —1. Однако запись кодовой комбинации в виде многочлена не всегда определяет длину кодовой комбинации п. Например, при п=5 многочлену х²+1 соответствует кодовая комбинация 00101. Поэтому при переходе к записи в виде кодовой комбинации необходимо дописывать нулевые старшие разряды.

Кодовые комбинации циклического кода описываются полиномами, обладающими определенными свойствами. Последние определяются свойствами и операциями той алгебраической системы, к которой принадлежит множество полиномов.

В циклических кодах разрешенными кодовыми комбинациями являются те, которые имеют нулевой вычет по модулю P_v(x), т. е. делятся на образующий полином без остатка. Из всех возможных полиномов степени п (2^п) только 2^к полиномов (к = п —r ) имеют нулевой вычет по модулю Р_г(х). Они и образуют множество разрешенных кодовых комбинаций циклического кода.

Циклические коды являются блочными, равномерными и линейными. Линейность кодов вытекает из того, что если кодовые слова принадлежат циклическому коду, то их линейная комбинация будет также принадлежать циклическому коду, т. е. обязательно делиться без остатка на образующий полином.

По сравнению с обычными линейными кодами на разрешенные кодовые комбинации циклического кода накладывается дополнительное ограничение: делимость без остатка на по­рождающий полином. Это свойство существенно упрощает аппаратурную реализацию кода.

Обнаружение ошибок в циклическом коде производится делением принятой кодовой комбинации на кодовую комбинацию образующего полинома (вид его должен быть известен на приеме). Остаток от деления R(x) играет роль синдрома. Если R(x) Ф0, то считается, что произошли ошибки. Если R(x)=0, то комбинация принята правильно.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: