Построение кодера и декодера циклического кода

Правило формирования проверочной группы (ФПГ):

1. Число ячеек памяти равно степени образующего полинома.

2. Число сумматоров на единицу меньше веса образующего полинома.

3. Сумматор ставится после каждой ячейки, начиная с нулевой, для которой существует
соответствующий член в полиноме. После ячейки, соответствующей старшему разряду,
сумматор не ставится.

В циклических кодах формирование проверочной группы элементов кодовой комбинации происходит делением полинома Q(x)x^r на образующий полином Рг(х). Так как операция деления в двоичном коде состоит из операций сдвига и сложения по модулю 2, то схемы кодирования содержат типовые элементы двоичной логики. Деление осуществляется схемами, которые называются регистрами с обратными логическими связями, или многократными линейными фильтрами. Принцип построения такого устройства рассмотрим на примере кода (9.5) с образующим полиномом Р(х)=х⁴+х+1. Пусть кодируется группа, информационный полином которой имеет вид Q(x)= x⁴+ х²+ х+ 1. Поскольку операция умножения на х^r означает добавление к соответствующей кодовой комбинации rнулей, то никакого специального устройства не требуется, а сдвиг на г=4 разряда осуществляется обычным регистром задержки. В данном примере регистр задержки имеет четыре ячейки. Деление производится в многотактном фильтре. Элементы информационной группы подаются на вход первой ячейки регистра, начиная со старшего разряда. Через четыре такта элемент старшего разряда появится на выходе регистра. С пятым тактом выходная ячейка будет свободна от поступления элементов информационной группы и в регистр вводится группа проверочных элементов, представляющая остаток от деления R(x).

Формирователь проверочной группы представляет собой сдвигающий регистр с обратными связями между ячейками. Эти связи реализуются через сумматоры по модулю 2. Указанная схема выполняет деление Q(x)x^r на Рг(х). Делимое в виде кодовой группы, представляющей полиномом Q(x)x^r, подаётся на вход сдвигающего регистра, а полином Рг(х) вводится в регистр в виде соответствующей подобранной структуры обратных связей через сумматоры. Проверочная группа элементов последовательно формируется на выходе регистра.

Число ячеек сдвигающего регистра выбирается равным степени образующего полинома, а число сумматоров по модулю 2 на единицу меньше его веса. В рассматриваемом примере вес полинома =3, следовательно, должно быть два сумматора.

ФПГ

Рис.3.1. Пример кодера циклического кода

 

В схеме РЗ - регистр задержки, обеспечивающий сдвиг информационной группы на четыре такта; ФПГ (формирователь проверочной группы) включает в себя регистры сдвига и сумматоры по модулю 2 в цепях обратной связи. В схеме имеются также два ключа К1 и К2, обеспечивающие необходимую последовательность работы схемы.. Исходное положение ключей: К1 - к ФПГ, К2 - разомкнут.

Принцип работы:

Первые 4 такта идёт одновременное заполнение регистра задержки и ФПГ. После 4-го такта ключи меняют своё положение. Следующие 5 тактов информационные разряды покидают кодер, одновременно с этим в ФПГ идёт процесс деления на образующий полином. После 9-го такта ключи вновь меняют своё положение. Вслед за информационными уходят проверочные разряды, одновременно с этим идёт заполнение ячеек регистров информационными разрядами следующей информационной комбинацией.

 

Другой вариант кодера для данного кода:

 

 

Рис.3.2.Пример другой схемы кодера циклического кода (9,5)

 

Ячейки в начале работы должны быть обнулены. Исходное положение ключей: К1 соединяет вход с выходом.

Принцип работы:

Первые 5 тактов информационные разряды уходят на выход, тем временем в ячейках кодера формируются проверочные процессы. После 5-го такта ключи меняют своё положение и вслед за информационными кодер покидают проверочные разряды.

 

 

Рис.3.3.Декодер с обнаружением ошибок.

 

Если информация пришла без ошибки то на выходе схемы или будет 0, если же на выходе будет 1, то произошла ошибка. Содержимое ячеек обнуляется, и переспрашивается.

Задача№1. Записать кодовую комбинацию циклического кода, если задан производящий полином 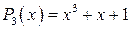, и кодовая комбинация, поступающая от источника сообщений . Нарисовать кодирующее и декодирующее устройство с обнаружением ошибок и “прогнать” через кодирующее устройство исходную кодовую комбинацию с целью формирования проверочных элементов.

Решение

Сначала аналитически определим разрешенную кодовую комбинацию, соответствующую данной информационной.

Запишем комбинацию в виде полинома:

Далее действуем по алгоритму, описанному в п. 3.3.

1.

2. Делим на образующий полином.

3. Полученный остаток 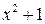прибавляем к : , что в двоичном виде соответствует комбинации 1001110.

Для построения кодера необходимо: три ячейки памяти, два сумматора. Схема кодера приведена на рисунке. В таблице приведенной ниже показаны состояния ячеек памяти кодера на каждом такте.

 

Рис 3.2 Схема кодера.

Таблица состояний кодера.

Такт	Регистр	ФПГ	выход

 

В начальный момент времени ключ K1 вниз, ключ K2 разомкнут. Три такта идёт заполнение обеих регистров. После третьего такта ключи меняют своё положение, информационные элементы уходят в канал, а в ФПГ идёт деление на образующий полином. На 7 такте деление закончилось, ключи меняют своё положение. После 7 такта проверочные символы уходят в канал, а в это время можно начинать передавать следующую информационную комбинацию.

 

 

Процесс декодирования аналогичен процессу кодирования. Схема декодера.

 

 

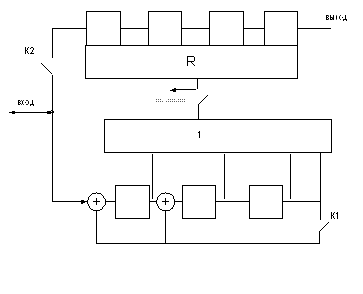
Рис 3.3 Схема декодера.

 

 

Задача 2

Вычислить вероятность неправильного приёма кодовой комбинации (режим исправления ошибок), в предположении, что ошибки в канале независимы, а вероятность неправильного приёма на элемент соответствует вычисленной в главе 2 (с учётом погрешности синхронизации и без учёта погрешности синхронизации).

Решение

Кодовая комбинация будет принята неправильно, если количество ошибок в ней превысит исправляющую способность кода . т. е. .

Заданный код имеет длину и число проверочных элементов, равное Такой код способен исправить только однократную ошибку. Таким образом, вероятность неправильного приёма складывается из вероятностей двух, трёх, четырёх, пяти, шести, семи ошибок. Так же можно вычислить эту вероятность по формуле:

 

,

где,

– вероятность безошибочного приёма блока;

– вероятность приёма блока с одной ошибкой;

и найдём, используя схему Бернулли:

,

,

где и – число сочетаний из 7 по 1 и из 7 по 0, соответственно.

Из курса теории вероятности нам известно, что: , а .

Подставив и в , и упростив, получаем формулу для определения вероятности неправильного приёма кодовой комбинации:

Остаётся подставить в это выражение вероятности ошибки на элемент, вычисленные во второй главе: 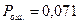без учёта погрешности синхронизации, с учётом погрешности синхронизации.

C учётом погрешности синхронизации:

C учётом погрешности синхронизации:

Ответ: ;

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: