 |
Линейные пространства. Определение. Примеры.
|
|
|
|
Линейные пространства
Множество V элементов любой природы x,y,z.. называется линейным (векторным) пространсвом, если для любых двух элементов x,y определена сумма x+y ∈ V, и для для x ∈ V и для а ∈ F, где F – некоторое числовое множество, определено произведение ах ∈ V и выполнены 8 аксиом.
·  , для любых
, для любых  (коммутативность сложения);
(коммутативность сложения);
·  , для любых
, для любых 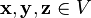 (ассоциативность сложения);
(ассоциативность сложения);
· существует такой элемент  , что
, что  для любого
для любого  (существование нейтрального элемента относительно сложения), называемый нулевым вектором или просто нулём пространства
(существование нейтрального элемента относительно сложения), называемый нулевым вектором или просто нулём пространства  ;
;
· для любого  существует такой элемент
существует такой элемент 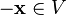 , что
, что  , называемый вектором, противоположным вектору
, называемый вектором, противоположным вектору 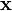 ;
;
· 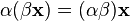 (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр);
·  (унитарность: умножение на нейтральный (по умножению) элемент поля F сохраняет вектор).
(унитарность: умножение на нейтральный (по умножению) элемент поля F сохраняет вектор).
·  (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров);
· 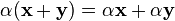 (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов).
Элементы векторного пространства будут называться векторами.
Примеры:
1 *1 *2 *3 линейные пространства свободных геом. Векторов
2 R(n)- в алгебраической трактовке R(n) можно рассмотреть, как совокупность строк, каждая их которых содержит n вещественных чисел.
3 Множество квадратных матриц
4 Множество всех многочленов Pm(f)
5 С [a,b] линейное пространство всех вещественных функций определённых и непрерывных на [a,b]
6 0 – линейное пространство, т.е о = {a}
14.Линейная зависимость и независимость векторов линейного пространства.
Векторы бывают линейно зависимыми или независимыми. Эти свойства определяют на основе следующих правил:
1) Векторы  называются линейно зависимыми, если найдутся такие действительные числа
называются линейно зависимыми, если найдутся такие действительные числа 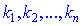 одновременно не равны нулю, при которых подтверждается равенство
одновременно не равны нулю, при которых подтверждается равенство
|
|
|
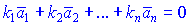
2) Если равенство
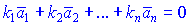
выполняется только при условии, что
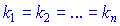
тогда векторы  называются линейно независимыми.
называются линейно независимыми.
Свойства
Если к линейно зависимой системе векторов  добавить несколько векторов, то полученная система будет линейно зависимой.
добавить несколько векторов, то полученная система будет линейно зависимой.
Если из линейно независимой системы векторов  исключить несколько векторов, то полученная система будет линейно независимой.
исключить несколько векторов, то полученная система будет линейно независимой.
Если в системе векторов  есть хотя бы один нулевой вектор, то такая система линейно зависимая.
есть хотя бы один нулевой вектор, то такая система линейно зависимая.
Если система векторов  линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов
линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов  линейно независима, то ни один из векторов не выражается через остальные.
линейно независима, то ни один из векторов не выражается через остальные.
15.Размерность линейного пространства. Базис.
Линейное пространство R называется n-мерным, если в нем существует n линейно независимых элементов, а любые (n +1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R.
Размерность пространства обозначают символом dim.
Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов.
Совокупность линейно независимых элементов  пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла
пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла 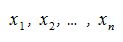 такие, что выполнено равенство
такие, что выполнено равенство
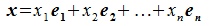
16.Координаты вектора в данном базисе. Линейные операции над векторами в координатной форме.
Координатами вектора m в базисе {е1, е2, е3 } называются коэффициенты разложения вектора m по векторам базиса, т.е. если m = хе1 + уе2 + zе3, то числа х, у, z - координаты вектора m. В этом случае будем записывать m(х, у, z).
При сложении векторов их координаты складываются, при умножении вектора на число его координаты умножаются на это число.
То есть все операции выполняются покоординатно.
|
|
|
17.Матрица перехода от одного базиса к другому. Связь между координатами вектора в разных базисах.
Ма́трицей перехо́да от базиса < a 1, a 2.. an > к базису < b 1, b 2.. bn > является матрица, столбцы которой —разложение векторов < b 1, b 2.. bn > в базисе < a 1, a 2.. an >.
Исходная квадратная матрица для матрицы перехода должна быть невыраженной.
Связь координат:
Рассмотрим произвольный элемент 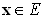 и запишем его разложение в двух заданных базисах
и запишем его разложение в двух заданных базисах  и
и 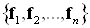 :
:


Перепишем равенства (3) в матричной форме:

То есть  , откуда с учётом формулы (2), получим:
, откуда с учётом формулы (2), получим:
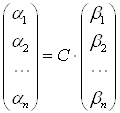 , (4)
, (4)
Где 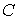 – матрица перехода от базиса
– матрица перехода от базиса  к базису
к базису 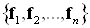 .
.
18. Непустое подмножество L линейного пространства V называется линейным подпространством пространства V, если:
1) u+v∈L ∀u,v∈Lu+v∈L ∀u,v∈L (подпространство замкнуто по отношению к операции сложения);
2) λv∈L ∀v∈Lλv∈L ∀v∈L и любого числа λ (подпространство замкнуто по отношению к операции умножения вектора на число).
Примеры линейных подпространств:
1. Пространство {o}, состоящее из одного нулевого вектора пространства V, является подпространством, т.е. {o}◃V{o}◃V.
2. Пусть, как и ранее, V1,V2,V3V1,V2,V3 — множества векторов (направленных отрезков) на прямой, на плоскости, в пространстве соответственно. Если прямая принадлежит плоскости, то V1◃V2◃V3V1◃V2◃V3. Напротив, множество единичных векторов не является линейным подпространством, так как при умножении вектора на число, не равное единице, получаем вектор, не принадлежащий множеству.
|
|
|


