Линейные преобразования линейных пространств.

Определение.

В линейном пространстве 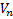задано преобразование A, если любому x принадлежащему 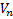, поставлен в соответствие определенный вектор А(х).

Преобразование A(x) линейное, если для любых x, y принадлежащих 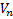и для α принадлежащей R будут выполняться сл. Равенства:

20. Матрица линейного преобразования. Связь между матрицами и линейными преобразованиями

Матрица линейного преобразования:

Связь матриц:

.

21, 23. Сложение и умножение линейных преобразований.

Линейные преобразования можно складывать и умножать.

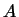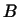Произведением линейных преобразований и называется преобразование , состоящее в последовательном выполнении сначала преобразования 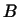, а затем преобразования .

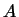Другими словами: означает, что для любого .

Произведение линейных преобразований есть линейное преобразование, т.е. удовлетворяет условиям 1 и 2 определения линейного преобразования. Действительно,

Первое равенство написано на основании определения произведения, второе на основании свойства 1 для 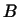, третье в силу того же свойства для 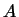и, наконец, четвертое опять-таки в силу определения произведения.

Аналогично показывается, что .

Если -- единичное преобразование, а 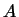-- произвольное, то легко проверить, что

Как обычно, определяем степени преобразования :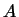

и т.д.

Как и для чисел, полагаем, по определению, 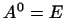. Очевидно, что

22. Умножение линейного преобразования на число

Из пункта 2 определения линейного пространства следует:

, где С-матрица преобразования.

Умножение в свою очередь, производится по правилу умножения просто матрица на число.

24) связь матриц лин. преобразований в разных базисах
Vn, A, e=(e1, e2,..., en), u=(u1, u2,..., in); u=eC; A(e)=eAe, A(u)=uAu;
A(u)=uAu=e(CAu), A(eC)=A(e)C=e(AeC) => e(CAu)=e(AeC)=> т.к. матрица С невырожденная и квадратная, то существует единственная обратная матрица
CAu=AeC
Au=C(-1)AeC
матрица линейного преобразования зависит от базиса

Th1 определитель матрицы лин. преобразований не зависит от базиса
|Au|=|C(-1)AeC|=|C(-1)|*|Ae|*|C|=|Ae|

25. Обратные преобразования.

Преобразование B называется обратным к A, если AB=BA=E, где E - единичное преобразование.

26. Собственные векторы и собственные значения линейного преобразования. Теорема о приведении линейного преобразования к диагональному виду.

 

Ненулевой вектор x ∈ L называется собственным вектором линейного преобразования, если существует такое число ⅄ ∈ K (K - мн-во чисел, на котором определено L), что выполняется неравенство: φ(x)=⅄x. При этом ⅄ - собственное значение (число) преобразования φ, отвечающее собственному вектору x.

 

Теорема.

Для того, чтобы матрица А линейного преобразования φ имела диагональный вид:

⅄1

∙ 0

A= ∙

0 ∙

⅄n

необходимо и достаточно, чтобы в Lⁿ существовал базис

Se={e1,…,en},

состоящий из собственных векторов φ и ⅄j являлось собственным числом, отвечающим вектору ej.

Доказательство.

Необходимость.

Пусть в некотором базисе Se={e1,…,en} матрица преобразования имеет вид:

⅄1

∙ 0

A= ∙

0 ∙

⅄n

Тогда для любого j (1≤j≤n) имеем φ (ej)=⅄jej и любой базисный вектор ej является собственным с собственным значением ⅄j.

Достаточность.

Пусть Se - базис из собственных векторов ej с собственными значениями ⅄j. Тогда имеем φ(ej)= ⅄j e Еj, откуда получаем матрицу преобразования.

28. Нахождение собственных векторов и собственных значений линейного преобразования.

1) Находим характеристическое уравнение матрицы. Для этого смотрим на исходную матрицу и записываем ее определитель, приравнивая его к нулю и вычитая из чисел главной диагонали ⅄.

2) Раскрываем определитель и решаем квадратное уравнение.

3) Корни - ⅄1 и ⅄2 и будут являться собственными значениями.

4) Подставим собственное значение в в однородную систему уравнений, составленную из матрицы определителя в пункте 1, подставляя ⅄.

5) Выражаем X через Y. Стараемся подобрать значение Y так, чтобы первая (X) координата собственного вектора была целой, положительной и минимальной.

6) Проверяем, что частное решение удовлетворяет всем условиям системы.

7) Если все верно, то получаем собственный вектор.

 

29. Инвариантность характеристического многочлена линейного преобразования.

Теорема. Характеристический многочлен не зависит от выбора базиса.

Доказательство.

Даны базисы e=(e1,e2,…,en) u=(u1,u2,…,un)

|Au-⅄E|=|C^-1AeC-C^-1⅄EC|=|C^-1(Ae-⅄E)C|=|C^-1||Ae-⅄E||C|=|Ae-⅄E|

Получим: |Au-⅄E|=|Ae-⅄E| => |A-⅄E|=P(⅄).

 

30) Теорема о приведении матрицы лин. преобразования к диагональному виду.
Th1 если спектр лин. преобразования является простым, т.е. все корни которого для данного характеристического многочлена различны т действительны, то лин. преобразование приводится к диагональному виду.
Th2 для того, чтобы матрица А приводилась к диагональному виду необходимо и достаточно, чтобы для каждого собственного значения лямбда кратности m, ранг матрицы А-лямбда*E равнялся (n-m), где n-число неизвеных, m-кратность корня.

(31 БИЛЕТ) ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.

Вектором называется направленный отрезок. Обозначается вектор , , 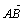, , AB, a (А – начало вектора, В – его конец).

Нулевым вектором (обозначается 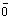) называется вектор, начало и конец которого совпадают.

Расстояние между началом и концом вектора называется его длиной, или модулем, или абсолютной величиной (обозначается , ).

Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых (обозначают , а также , если векторы сонаправлены, и , если они противоположно направлены).

Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Два вектора называются равными, если они сонаправлены ( ) и имеют равные длины ( ). Обозначают .

Для каждого вектора , отличного от нулевого вектора, существует противоположный вектор, который обозначается и удовлетворяет условиям: , .

 

Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.

Сложение векторов. Пусть и – два произвольных вектора. Возьмем произвольную точку О и построим вектор ; затем от точки А отложим вектор . Вектор , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается 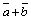(рис. 1).

 

 

Рис. 1

Ту же сумму можно получить иным способом. Отложим от точки О векторы и . Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор – диагональ параллелограмма – является суммой векторов и (рис. 2).

 

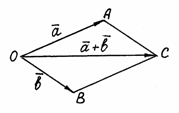
Рис. 2

Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).

 

Рис. 3

Вычитание векторов. Разностью векторов и называется такой вектор 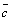, который в сумме с вектором дает вектор : Û .

Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).

 

Рис. 4

Таким образом, если на векторах и , отложенных из общей точки О, построить параллелограмм ОАСВ, то вектор , совпадающий с одной диагональю, равен сумме 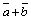, а вектор , совпадающий с другой диагональю, – разности (рис. 5).

 

Рис. 5

Умножение вектора на число. Произведением вектора на действительное число называется вектор (обозначают ), определяемый следующими условиями:

1) ,

2) 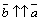при и при .

Очевидно, что при .

Построим, например, векторы и для заданного вектора (рис. 6).

Рис. 6

Из определения следует: два вектора и коллинеарны тогда и только тогда, когда имеет место равенство :

(2.1)

Свойства линейных операций:

1) ;

2) ;

3) ; ;

4) ;

5) ;

6) ;

7) ; ;

Пусть дан вектор . Ортом вектора (обозначается ) называется вектор единичной длины, сонаправленный с вектором .

Очевидно, для любого вектора .

 

(32 БИЛЕТ) БАЗИС.КООРДИНАТЫ ВЕКТОРА.ЛИНЕЙНЫЕ ОПЕРАЦИИ В КООРДИНАТНОЙ ФОРМЕ.

 

Базис - любая упорядоченная система из n линейно независимых векторов пространства .

Обозначение:

Для каждого вектора существуют числа такие что

Числа называются координатами вектора в базисе () (определяются однозначно), X = (x) - координатный столбец вектора в этом базисе. Употребляется запись:

Операции в координатной форме:

Равенство векторов и линейные операции (сложение векторов и умножение вектора на число) удобно представлять в координатной форме. При этом справедливы следующие свойства:

1. Равные векторы имеют равные координаты (в одном и том же базисе).

2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.

3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.

4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.

 

 

(33 БИЛЕТ) ЛИНЕЙНАЯ ЗАВИСИМОСТЬ И НЕЗАВИСИМОСТЬ ВЕКТОРОВ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ЛИНЕЙНОЙ ЗАВИСИМОСТИ.

 

 

1)Если линейная комбинация может представлять собой нулевой вектор тогда, когда среди чисел есть хотя бы одно, отличное от нуля, то система векторов называется линейно зависимой.

2) Если линейная комбинация представляет собой нулевой вектор только тогда, когда все числа равны нулю, то система векторов называется линейно независимой.

Геометрический смысл л.з.:

1. Система, состоящая из двух (или более) коллинеарных векторов, линейно зависима.

С другой стороны, если два вектора линейно зависимы, один из них получается умножением другого на число, а тогда векторы коллинеарны.

2. Система, состоящая из двух векторов, тогда и только тогда линейно зависима, когда векторы коллинеарны.

3. Система, состоящая из трек векторов, тогда и только тогда линейно зависима, когда данные три вектора компланарны.

 

 

(БИЛЕТ 34) СИСТЕМЫ КООРДИНАТ НА ПРЯМОЙ, НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ. ПРЯМОУГОЛЬНАЯ СИСТ. КООРДИНАТ.

Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство) образуется тремя взаимно перпендикулярными осями координат , 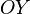и . Оси координат пересекаются в точке 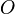, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. 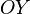— ось абсцисс, — ось ординат, — ось аппликат.

Положение точки в пространстве определяется тремя координатам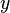и , и 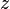. Координата равна длине отрезка , координата 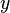— длине отрезка , координата 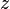— длине отрезка в выбранных единицах измерения. Отрезки , и определяются плоскостями, проведёнными из точки параллельно плоскостям , и соответственно.

Координата называется абсциссой точки ,

координата 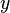— ординатой точки ,

координата 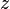— аппликатой точки .

Символически это записывают так:

или

 

(БИЛЕТ 35) ВЫРАЖЕНИЕ КООРДИНАТ ВЕКТОРА ЧЕРЕЗ КООРДИНАТЫ НАЧАЛА И КОНЦА.

Возь­мем точку .

Рис. 1. Ил­лю­стра­ция к при­ме­ру

Век­тор на­зы­ва­ет­ся ра­ди­ус-век­то­ром точки 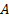и в точ­но­сти равен век­то­ру .

Ко­ор­ди­на­ты точки 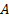равны со­от­вет­ству­ю­щим ко­ор­ди­на­там век­то­ра .

Рас­смот­рим те­перь век­тор , у ко­то­ро­го на­ча­лом может быть про­из­воль­ная точка, от­лич­ная от на­ча­ла ко­ор­ди­нат.

Дано: ,

Найти: ко­ор­ди­на­ты век­то­ра .

Рис. 2. Ил­лю­стра­ция к при­ме­ру

Мы уже знаем, как на­хо­дить ко­ор­ди­на­ты век­то­ра с на­ча­лом в точке . По­стро­им век­то­ры и и най­дем их ко­ор­ди­на­ты (рис. 3).

Рис. 3. Ил­лю­стра­ция к при­ме­ру

Поль­зу­ясь преды­ду­щим пра­ви­лом, утвер­жда­ем, что ко­ор­ди­на­ты век­то­ра сов­па­да­ют с ко­ор­ди­на­та­ми точки 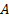, а ко­ор­ди­на­ты век­то­ра сов­па­да­ют с ко­ор­ди­на­та­ми точки :

.

Век­тор равен раз­но­сти век­то­ров и :

Пра­ви­ло. Каж­дая ко­ор­ди­на­та век­то­ра равна раз­но­сти со­от­вет­ству­ю­щих ко­ор­ди­нат его конца и на­ча­ла.

36) Скалярное произведение и необходимое и достаточное условие ортогональности 2-х векторов
Скалярным произведением 2-х векторов называется число, равное произведению их длин на косинус угла между ними.
Св-ва скалярного произведения:
*скалярное произведение равно 0, когда один из векторов является нулевым или векторы ортогональны
*ab=ba(коммутативность)
*(лямбда*a)b=a(лямбда*b)=лямбда*(ab)
*a(b+c)=ab+ac
*|a|^2=|a|*|a|
Есть ортонормирование базис i, j, k.
a=x1*i+y1*j+z1*k a{x1;y1;z1}
b{x2;y2;z2}
a*b=x1*x2+y1*y2+z1*z2
Th1 для того, чтобы 2 ненулевые вектора были ортогональны необходимо и достаточно, чтобы скалярное произведение равнялось 0.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: