 |
Условия параллельности и перпендикулярности прямой и плоскости.
|
|
|
|
В случае параллельности прямой линии
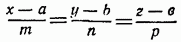
и плоскости
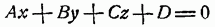
угол между ними равен нулю, следовательно 
и формула (12) дает искомое условие
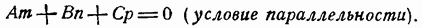(13)
Замечание. Это условие получится сразу, если заметим, что векторы 
и 
перпендикулярны, и, значит, их скалярное произведение равно нулю.
Условие перпендикулярности прямой и плоскости совпадает с условием параллельности этой прямой иперпендикуляра к плоскости, т. е. будет:
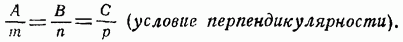
Задача. Составить уравнение геометрического места всех прямых, проходящих через точку (a, b, c) параллельно плоскости
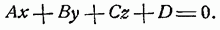
Уравнение любой прямой, проходящей через точку (a, b, c), будет:
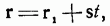
где 
— радиус-вектор данной точки, a s есть тот вектор, которому прямая параллельна. Так как искомая прямая должна быть перпендикулярна к вектору n 
, то должно иметь место
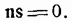
Умножая уравнение прямой на вектор n, получим:
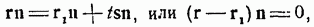
так как ns=0 Уравнение 
определяет плоскость, проходящую через точку с радиусом-вектором , перпендикулярно к вектору n. Переводя его в координатную форму, будем иметь:
Замечание. Эту же задачу можно решить, не прибегая к векторному методу. Уравнения любой прямой, проходящей через точку 
, суть:
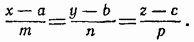
Условие параллельности искомых прямых и данной плоскости выразится равенством
Заменяя в последнем условии m, n, p величинами x-a, y-b и z-c, им пропорциональными, получаем:
Билет 61. Эллипсоиды. Гиперболоиды. Параболоиды
Эллипсоид
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением 
a > 0, b > 0, c > 0, называется эллипсоидом.
Свойства эллипсоида.
- Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что
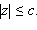
- Эллипсоид обладает
- центральной симметрией относительно начала координат,
- осевой симметрией относительно координатных осей,
- плоскостной симметрией относительно начала координат.
- В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.
|
|
|
Параболоид
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением 
a > 0, b > 0, называется эллиптическим параболоидом.
Свойства эллиптического параболоида.
- Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.
- Эллиптический параболоид обладает
- осевой симметрией относительно оси Oz,
- плоскостной симметрией относительно координатных осей Oxz и Oyz.
- В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением 
a > 0, b > 0, называется гиперболическим параболоидом.
Свойства гиперболического параболоида.
- Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
- Гиперболический параболоид обладает
- осевой симметрией относительно оси Oz,
- плоскостной симметрией относительно координатных плоскостей Oxz и Oyz.
- В сечении гиперболического параболоида плоскостью, ортогональной оси координат Oz, получается гипербола, а плоскостями, ортогональными осям Ox и Oy, – парабола.
- Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.
Гиперболоид
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением 
a > 0, b > 0, c > 0, называется однополостным гиперболоидом.
|
|
|
Свойства однополостного гиперболоида.
- Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
- Однополостной гиперболоид обладает
- центральной симметрией относительно начала координат,
- осевой симметрией относительно всех координатных осей,
- плоскостной симметрией относительно всех координатных плоскостей.
- В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением 
a > 0, b > 0, c > 0, называется двуполостным гиперболоидом.
Свойства двуполостного гиперболоида.
- Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что
и неограничен сверху. - Двуполостный гиперболоид обладает
- центральной симметрией относительно начала координат,
- осевой симметрией относительно всех координатных осей,
- плоскостной симметрией относительно всех координатных плоскостей.
- В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, при
получается эллипс, при 
– точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, – гипербола.
Поверхности вращения
Поверхностью вращения называется поверхность, образованная вращением какой-либо плоской линии вокруг прямой, лежащей в плоскости этой линии. Для вывода уравнения поверхности вращения необходимо выбрать систему координат. Чтобы уравнение поверхности вращения выглядело проще, ось вращения принимают за одну из координатных осей.
|
|
|
