 |
Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности.
|
|
|
|
Угол между двумя пересекающимися прямыми – это мера меньшего из четырех углов, образованных этими прямыми.
Усл-е паралл-ти:
Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов.
Для случая, когда прямые заданы уравнениями в общем виде, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны.
Усл-е перпен-ти:
В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.
Если уравнения прямых заданы в общем виде, то условие их перпендикулярности заключается в выполнении равенства: A 1 A 2 + B 1 B 2 = 0
47.Векторно-параметрическое уравнение плоскости. Параметрические уравнения плоскости.
Векторно-параметрическое уравнение:
P: r-r0 = t p + sq, (t,s) Î R
M0 Î P (начало координат), векторы p и q направляющие вектора плоскости Р.
t,s могут изменяться от -∞до +∞.
Параметрические уравнения плоскости.
M0M = t p + sq
r = r0 + tp + sq
в координатной форме 
48. плоскость как поверхность 1-го порядка. Нормальное уравнение плоскости.
Любая плоскость есть поверхность 1-го порядка.
Нормальное уравнение плоскости. xcosα + ycosβ + zcosg - p = 0
При чем cos2α + cos2β + cos2g = 1
n = (cosα, cosβ, cosg) – нормальный вектор
49. общее уравнение плоскости, приведение общего уравнения к нормальному виду.
Общее уравнение плоскости Ax + By + Cz + D =0
Чтобы привести обще уравнение к нормальному виду, нужно поделить обе части на
|
|
|
, при чем берем со знаком + когда D<0, а cо знаком – когда D>0
50. уравнение плоскости по точке и нормальному вектору, векторное уравнение плоскости. Связка плоскостей.
уравнение плоскости по точке и нормальному вектору 
=0
векторное уравнение плоскости (r-r0, p, q) = 0, N=[ p,q]
Связка плоскостей это совокупность всех плоскостей, проходящих через одну точку М0 – центр связки. Если М0 (x0,y0,z0) то она может быть задана в виде A(x-x0) + B(y-y0) + C(z-z0) + D =0, где A,B,C – произвольные действительные числа.
| 51) Уравнение плоскости, проходящей через 3 точки. Уравнение плоскости в отрезках. M1(x1;y1;z1) M2(x2;y2;z2) M3(x3;y3;z3) М(x;y;z)-произвольная точка плоскости |x-x1 y-y1 z-z1| |x2-x1 y2-y1 z2-z1|=0 |x3-x1 y3-y1 z3-z1| уравнение плоскости через 3 точки | ||
| |x-a y z| |-a b 0|=0 |-a 0 c| (x-a)bc-y(-ac)+zab=0 x/a+y/b+z/c=1 уравнение плоскости в отрезках |
Угол между двумя плоскостями. Условие параллельности и перпендикулярности двух плоскостей.
Угол между двумя плоскостями.
Пусть уравнения данных плоскостей будут:
Углом между двумя плоскостями будем называть любой из двух смежных двугранных углов, образованных этими плоскостями (в случае параллельности плоскостей угол между ними можно считать равным 0 или π по желанию). Один из этих двугранных углов равен углу φ между векторами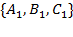 
и 
перпендикулярными к данным плоскостям. Угол φ определяется согласно формуле:
Замечание. Вывод формулы можно выполнить, не прибегая к векторам. Чтобы вычислить угол φ между плоскостями, заданными уравнениями плоскостей, заметим, что один из двух смежных двугранных углов, образованных плоскостями, равен углу между перпендикулярами к этим плоскостям из начала координат. Написав нормальные уравнения плоскостей в виде
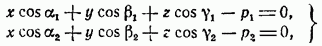
имеем:
Так как
то, подставляя эти значения в равенство , найдем:
В этой формуле можно брать любой знак (+ или -) что соответствует выбору одного из двух смежных двугранных углов.
|
|
|
|
|
|
