И поверхностей алгебраическими полиномами

ИНТЕРПОЛЯЦИЯ КРИВЫХ

2.1. Основные способы моделирования кривых. Интерполяция и аппроксимация

Основной задачей геометрического моделирования является построение геометрических объектов, исходя из их требуемых геометрических, физико-механических и эстетических свойств. Под геометрическими условиями понимают следующие:

- прохождение моделируемой кривой через заданную точку (t_i,х_i): P(t_i)=x_i;

- непрерывность кривой P (t) в месте её сопряжения t_i с другой кривой: P(t_i)=Q(t_i);

- равенство некоторой производной порядка j моделируемой кривой P(t) в точке t_i некоторой заданной величине: P ^j(t_i)=P_i ^j ;

- гладкость порядка j (непрерывность производной данного порядка) моделируемой кривой P (t) в месте её сопряжения t_i с другой кривой Q(t): P^j(t_i)=Q ^j(t_i);

- равенство радиуса кривизны моделируемой кривой r (t) в точке t_i заданному значению: r (t_i) = r _i

- и т.д.

Каждое из перечисленных условий задаёт ровно одно геометрическое ограничение на моделируемую кривую, которая обычно является полиномом. Из этого следует, что на основе условия можно записать одно уравнение, кото-рое содержит неизвестные значения коэффициентов поли-нома. Эти коэффициенты являются параметрами синтеза, полностью характеризующими моделируемую кривую.

Если требуется точное выполнение всех наложенных геометрических условий, то такое построение называется

интерполяцией. Если условия выполняются приближенно, то - аппроксимацией.

Интерполирование кривой всегда возможно в том случае, когда количество параметров синтеза (как правило, это численные коэффициенты, входящие в формулу кривой) равно либо превышает число геометрических условий, наложенных на неё. В этом случае по геометрическим условиям всегда можно составить систему уравнений относительно параметров синтеза, которая имеет хотя бы одно решение. Иначе (количество параметров синтеза меньше числа геометрических условий) может иметь место только аппроксимация кривой по заданным условиям. Как будет показано ниже, это правило нарушается в тех случаях, когда имеет место дублирование геометрических условий.

При интерполировании моделируемая кривая `P(t) на некотором сегменте 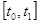должна точно удовлетворять заданным геометрическим условиям (прохождение через точки, условия на производные и т.д.). Наиболее рас-пространенным является случай линейного интерполиро-вания, когда искомая кривая имеет вид:

, (2.1)

где - постоянные коэффициенты, - семейство функций, образующих базис.

Определение. Функции образуют базис, если любая достаточно гладкая кривая `P(t) может быть единственным образом выражена через них в виде (2.1).

Единственность представления `P(t) в форме (2.1) равно-сильна выполнению следующего условия: , при , то есть,

тождественно нулевая функция не может быть представ-лена разложением с ненулевыми коэффициентами. Семей-ство функций {j_i(t)} обычно задают заранее. Наиболее час-то в качестве {j_i(t)} используют степенные функции: j_i = xⁱ, i=0,1,…,n. В этом случае искомая кривая `P(t) вида (2.1) является алгебраическим полиномом с неизвестными коэф-фициентами:

(2.2)

Решение задачи интерполирования при заданном базисе {j_i(t)} сводится к решению системы уравнений, получаемой при подстановке заданных геометрических условий в выражение (2.1). Метод решения, при котором коэффици-енты разложения `a={a₀,a₁,…,a_n) определяются непосред-ственным решением этой системы, называется методом неопределенных коэффициентов.

Замечание. При произвольном задании геометрических условий (по количеству и виду) для точного решения зада-чи интерполирования в качестве переменных должны быть приняты и максимальная степень полинома n и вектор его неизвестных коэффициентов `a.

Другим распространённым способом интерполирования является построение кусочных кривых. В этом случае для моделируемой кривой не существует единого представле-ния (например, как (2.1)) и она состоит из отдельных по-следовательных участков. Данный подход используется при интерполировании алгебраическими сплайнами.

В ряде случаев при моделировании кривых использова-ние интерполирования либо невозможно, либо нежелатель-но. В первом случае это обычно связано с тем, что макси-мальная степень зафиксирована либо ограничена и ее “ не хватает” для точного выполнения всех геометрических

условий. Во втором случае кривая, полученная интер-полированием, имеет вид, неудовлетворительный с кон-структивной или эстетической точки зрения. Выход за-ключается в построении приближенных кривых с аппрок-симацией заданных геометрических условий.

При нахождении аппроксимирующей кривой ` P(t) вида (2.1) в случае заданного базиса {j_i(t)} возможны два основ-ных подхода:

1. Варьируются геометрические условия, а коэффициенты `a определяются по ним однозначно. Примером такого под-хода являются кривые Безье.

2. Геометрические условия принимаются неизменными, а варьируются величины коэффициентов `a (например, при аппроксимации с помощью алгебраических полиномов).

В качестве критерия оптимальности выполненной ап-проксимации в зависимости от решаемой задачи могут быть приняты:

- численные характеристики близости кривой ` P(t) к заданным геометрическим условиям;

- эстетический вид получаемой кривой, который субъек-тивно оценивается проектировщиком.

В качестве численной меры близости моделируемой кривой ` P(t) к заданной на интервале [a,b] функции f(t) наиболее часто применяют две характеристики:

1) максимальное абсолютное отклонение

, (2.3 a)

2) среднеквадратичная ошибка

_. (2.4 а)

Более точно отражают геометрическую близость кривых разности, взятые не по параметру, а по нормали к исходной кривой, однако вычисление таких ошибок более сложно. В

том случае, если моделируется кривая, которая должна пройти вблизи заданных точек (x(t₁), x(t₂),…, x(t_n)),то критерии (2.3 а) и (2.4 а) заменяют, соответственно, на сле-дующие величины:

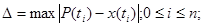(2.3 б)

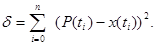(2.4 б)

В обоих рассмотренных случаях требуется за счёт варьирования величин коэффициентов достичь мини-мально возможной величины соответствующей численной характеристики отклонения. В математической форме кри-терии оптимального синтеза аппроксимируемых кривых по обеим характеристикам близости принимают одинаковый вид:

d(a_{0, …,} a_n) ® min; D (a_{0, …,} a_n) ® min.

(a_{0, …,} a_n) (a_{0, …,} a_n)

Очевидно, интерполирование может рассматриваться как частный случай аппроксимации, при котором величина отклонения равна нулю.

Задачи.

1. На моделируемую кривую у(х) в узлах х₀ , х₁ наложены следующие геометрические условия: у(х₀) = у₀; у¢ (х₀)=у¢₀ ; у¢¢ (х₀) =у¢¢₀; у(х₁) = у₁; у¢ (х₁)=у¢₁ . При каком количестве параметров синтеза всегда возможна интерполяция кривой, а при каком – аппроксимация?

2. В узлах х₀ , х₁ , х ₂ на моделируемую кривую, форма кото-рой задана шестью коэффициентами, наложены следующие геометрические условия: у(х₀) = у₀; у¢ (х₀)=у¢₀; у(х₁) = у₁; у¢ (х₁)=у¢₁ ; у¢¢(х₁) = у¢¢₁; у(х₂) = у₂; у¢ (х₂)=у¢₂ . Возможна ли в общем случае интерполяция данной кривой?

3. Сколько и каких геометрических условий необходимо наложить на алгебраическую кривую у(х), чтобы она кос-нулась в точках х = 0 и х = 1 оси х?

 

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: