 |
Интерполирование кривых с помощью алгебраических полиномов канонического вида
|
|
|
|
Алгебраической кривой (полиномом степени k) назы-вают выражение вида
P (t)=C0+C1t+C2t2+…+Ck tk, (2.5)
где t - параметр кривой. Выражение (2.5) называется кано-ническим видом полиномов. При его использовании (по схеме Горнера) затрачивается минимальное число опера-ций в расчётезначений P (t).
В общем случае интерполирования постановку задачи можно сформулировать следующим образом: построить полином, у которого:
1) соответствующая кривая проходит через заданные точки `P0,`P1,…,`Pn;
2) в некоторых точках `Pi полинома производные его до некоторой степени j должны принимать заданные значения:
P¢(ti)=Pi¢,
...
P j(ti)=Pi j ,
где ti - величина параметра в рассматриваемой точке,
Pi1(ti), …, Pi j(ti) – значения соответствующих производных.
В явной форме (в виде готовой формулы, не требую-щей предварительного составления и решения уравнений) решение рассмотренной задачи дают интерполяционные полиномы Лагранжа (Ньютона) и Эрмита. Однако вслед-ствие сложного вида этих полиномов вычисление значений по ним требует выполнения значительно большего числа операций по сравнению с расчётом по канонической фор-муле (2.5) (при этом результаты вычислений по обеим формулам совпадают в силу того, что искомое решение единственно). Поэтому вначале рассмотрим решение зада-
чи для канонического случая. При интерполировании про-странственных кривых в параметрическом виде задача сводится к построению зависимостей x(t),y(t),z(t) по всем трем координатам, в явном – к построению функций y(x), z(x). На плоскости строятся, соответственно, х(t), y(t) или у(x).
Поскольку построение полиномов по каждой коорди-нате производится одинаково, то ограничимся рассмот-рением интерполирования полинома Р(x) степени k в явном виде на некотором наборе узлов x0, x1,…, xn. Обычно для интерполирования используется полином с минимально возможной степенью k. При расчете минимального k исходят из следующих соображений: число неизвестных коэффициентов С0, C1, …,Ck в полиноме равно (k+1). Число геометрических условий, которые должны быть выполнены, складывается из:
|
|
|
1) количества заданных точек `P0,`P1,…,`Pn – их число равно (n+1);
2) общего числа производных  , заданных в этих точках.
, заданных в этих точках.
Решение задачи интерполирования всегда существует и является единственным, если k+1 = n+1+  . При выполнении этого условия число неизвестных равно числу уравнений. Отсюда следует:
. При выполнении этого условия число неизвестных равно числу уравнений. Отсюда следует:
k=n+  . (2.6)
. (2.6)
После определения k решается задача об определении коэффициентов полинома. Для этого составляется система из k уравнений следующего вида. Каждое условие первого типа y(xi) = yi при подстановке x = xi дает уравнение вида:
C0+C1xi+C2xi2+…+Ckxik=yi.
Для раскрытия условия на первую производную y¢(xi) = yi¢ выполняем подстановку x = x1 в производную 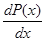 . Получаем уравнение: C1+2C2xi +…+kCkxik-1 = y i¢.
. Получаем уравнение: C1+2C2xi +…+kCkxik-1 = y i¢.
Производные более высоких порядков раскрыва-ются аналогично. Итоговую систему уравнений можно представить в виде:
A`C=`Y, (2.7)
где ` C=(C0,C1,…,Ck) – искомый вектор коэффициентов полинома,
`Y – вектор заданных точечных значений функции и ее производных,
A – матрица коэффициентов.
Искомый вектор неизвестных коэффициентов равен:
C=A-1 *`Y, (2.8)
где A-1 – матрица, обратная к А.
Пример. Заданы: 1) значения полинома в трех узлах: y(x0) = y0; y(x1)=y1; y(x2)=y2 и 2) значение первой производной в узле x0 : y¢(x0)=y0¢. Необходимо построить интерполирую-щий полином наименее возможной степени k.
Решение.
1.Определение степени полинома k. Число n=2, суммарное число заданных значений производных  =1. Следова-тельно, по формуле (2.6) k=3 и полином имеет вид:
=1. Следова-тельно, по формуле (2.6) k=3 и полином имеет вид:
P (x)=C0+C1x+C2x2+C3x3,
где (С0, C1, C2, C3) - постоянные коэффициенты.
2.Определение коэффициентов полинома. Из условий вида 1) подстановкой вместо х значений х0, х1, х2 получаем урав-нения
|
|
|
C0+C1x0+C2x02+C3x03 = y0;
C0+C1x1+C2x12+C3x13 = y1 ;
C0+C1x2+C2x22+C3x23 = y2 .
Из условия вида 2) подстановкой х = х0 в P¢(x) = C1 + 2C2x + 3C3x2 получаем уравнение C1 + 2C2x0 + 3C3x02 = y0¢.
Объединяя полученные уравнения, получаем систему вида (2.7), где
 ;
;  ;
;  .
.
Решением системы является вектор ` C=A-1 *`Y.
Замечание. При специальном задании геометрических условий возможны случаи, когда реальная степень поли-нома меньше значения, задаваемого формулой (2.6). На-пример, если в приведенном выше примере задать условия вида:
y(1)=0; y(2)=1; y(3)=2; 2) y¢(1)=1; то при этом
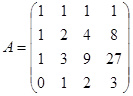 ;
; 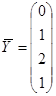 ;
; 
 ; P(x) = x-1; k = 1 < 3.
; P(x) = x-1; k = 1 < 3.
Таким образом, в данном частном случае реальная сте-пень интерполирующего полинома равна 1. Геометричес-кий смысл примера понятен из Рис.2.1: точки ` Р0, ` Р1, ` Р2 лежат на прямой y=(x-1), угол наклона производной y¢(x0) также равен углу наклона этой прямой, поэтому в данном случае k=1.

Рис.2.1
Если рассматривать частный случай
y(1)=1; y(2)=1; y(3)=1; 2) y¢(1)=0;
то векторы `Y и `С будут следующими:
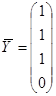 ;
; 
Интерполирующий полином примет вид: P(x) = 1. В данном случае реальное значение k=0, т.к. все точки лежат на прямой y=1 и угол наклона производной равен 0 (Рис. 2.2).

Рис. 2.2
В обоих приведенных примерах имеет место дублиро-вание геометрических условий, поскольку некоторые из них оказываются излишними, описывающими объект, уже полностью определённый предыдущими условиями. Рас-смотренные примеры показывают, что окончательное зна-чение степени полинома k может быть уточнено только после расчета его коэффициентов.
Задачи.
1. Найти степень полинома k и матрицу А (по возможности в численном виде) для определения коэффициентов поли-нома `С =(C0, C1, …,Ck) для следующих наборов геометри-ческих условий:
а) Задача 1 из п.2.1,
б) n=1; х0 = -1; х1 =1;
у(-1) = 1; у¢(-1) = 2; у¢¢ (-1)=3; у(1) = 1,5; у¢(1);
в) n=3; х0 = 0; х1 = 1; х2 =2; х3 =3;
у(х0) = 0; у (х1)= 2; у(х2) =5; у (х3)=6;
г) n=2; х0 = -1; х1 = 0; х2 =1;
у(х0) = -2; у¢(х0) = 2; у(х1)= у¢(х1)=1; у(х2) = 1,5; у¢(х2) =0;
д) n=2; х0 = 1; х1 =3; х2 =4;
у(х0)=у¢(х0)=1; у(х1)=2; у¢(х1)=у¢¢(х1)=0; у(х2)=1; у¢(х2)=- 2.
|
|
|


