 |
Интерполирование поверхностей
|
|
|
|
2.5.1. Интерполирование по однократным узлам. Билинейные поверхности
Кривые, как плоские, так и пространственные, явля-ются функциями одного параметра. Поверхности всегда описываются двумя.
Рассмотрим вначале интерполирование по однократ-ным узлам и найдем двумерный аналог полинома Лагран-жа. Пусть на плоскости Oxy задана прямоугольная сетка (xi,уj) (i = 0,1,..., n; xi ¹ xk при i¹ k, j = 0,1,..., m; yj ¹ ys при j¹ s). В узлах сетки заданы значения координаты по оси z некоторой поверхности z (x i, у j) = z i j. Необходимо по-строить квадратичную форму L(x,у) минимально возмож-
ной степени, для которой L(xi,уj)=zi j,(i = 0,1,..., n; j = 0,1,..., m), т.е. в узлах сетки её значения равны заданным величинам z (xi, уj).
Решение задачи существует и единственно. Так как общее число геометрических условий по оси х равно (n+1), а по оси у – (m+1), то искомая форма будет иметь степени по этим осям, соответственно, не выше n и m. В скалярном виде её можно представить следующим образом:
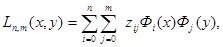 (2.20)
(2.20)
где Ф i (x), Ф j (y) – функции Лагранжа по переменным х,у, построенные по соответствующим координатам узлов (xi, уj), (i = 0,1,..., n; j = 0,1,..., m). Назовём её квадратичной формой Лагранжа.
В векторном виде квадратичную форму (2.20) можно представить как:
L n,m (x,y) = `ФТ(х) Z`Ф(y), (2.21)
где Z – прямоугольная матрица ((n+1) ´ (m+1)), содержащая значения z i j, (i = 0,1,..., n; j = 0,1,..., m):
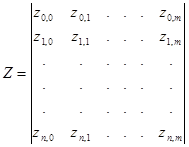 |
`ФТ(х) = (Ф0 (х), Ф1 (х),..., Фn (х)) - вектор-строка значе-ний функций Лагранжа по оси х;
`Ф(y) = (Ф0 (y), Ф1 (y),..., Фm (y)) - вектор-столбец зна-чений функций Лагранжа по оси у.
Рассмотрим интерполирование на прямоугольном участке [x0,x1]´ [у0, y1]. В его граничных точках заданы по одному геометрическому условию: z(x0,у0)= z00, z(x1 ,у0) =z10, z(x0, у1)= z01 , z(x1 ,у1) =z11 . Минимальные степени квадратичной формы S(x,y) по переменным х,у равны еди-нице. Явное решение для S(x,y) проще всего задать в век-торной форме при помощи функций Лагранжа:
|
|
|
S (x,y) =`Ф(x)Т Z`Ф(у); (2.22 а)
где `Ф(x)=((x1 –x) / (x1 -x0), (x-x0) / (x1 -x0 ));
`Ф(у)=((y1 –y) / (y1 -y0), (y-y0) / (y1 -y0));
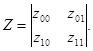 |
Переходя, как и в одномерном случае, к безразмер-ным нормированным переменным tх= (x - x0)/(x1 - x0 ) и tу = (у - y0)/(y1 - y0 ) и используя матрицу МЛ, решение для S(x,y) можно представить в виде:
S(tx,ty) = (MЛ`Тх1) Z (MЛ`Тy1), (2.22 б)
где (МЛ`Тх1) Т – вектор – строка,
В том случае, если участок поверхности интерполиру-ется по четырём произвольным однократным узлам (не об-разующим прямоугольник на плоскости хОу), то такую по-верхность, называют билинейной, поскольку она линейна в отдельности по каждой переменной (как и поверхность (2.22)). Рассмотрим билинейную поверхность более подроб-но. Допустим, она строится по точкам {`Pj} = {`P1,`P2,`P3, `P4}. Для параметров u и v вводят локальную систему ко-ординат, начало которой помещают в точке `P1, ось u на-правляют от `P1 к `P2 , а ось v - от `P1 к `P3 Масштабы по осям u и v вводят таким образом, чтобы значения u=1 и v=1 параметры получали в точках `P2,`P3.
Математическое задание координат точек, лежащих на осях и внутри поверхности, имеет вид:
` S(u,v) =`P1 × (1-u) × (1-v) +`P2 × u × (1-v) +`P3 × v × (1-u) +
+`P4 × u × v, где 0 £ u, v£ 1. (2.23)
При этом: `S(0,0)=`P1;`S(1,0)=`P2;`S(0,1)=`P3;`S(1,1)=`P4.
При фиксации одного из параметров происходит сни-жение размерности объекта (поверхности) на единицу и он превращается в линию (линию уровня):
`S(u,v0 =const) – линия соответствующая уровню v= v0;
`S(u0 =const,v) – линия соответствующая уровню u= u0.
Поскольку билинейные поверхности линейны в от-дельности по каждому параметру, то их линии уровня являются отрезками прямых (Рис 2.3).

Рис.2.3
Функция Q на языке Autolisp для построения линий уровня поверхности, интерполированной по 4 точкам, и их проекций на плоскость z=0, а также соответствующая отладочная функция приведены в Приложении.
|
|
|
2.5.2. Интерполирование по двукратным узлам
Рассмотрим интерполирование поверхностей по дву-кратным узлам. Допустим, на плоской прямоугольной сет-ке (xi, уj), (i = 0,1,..., n; j = 0,1,..., m) наряду со значениями координаты по оси z некоторой поверхности z (xi, уj) = z i j заданы также значения её частных производных по x, у: z¢х (xi, уj) = zхi j, z¢у (xi, уj) = zуi j, а также смешанной производной z¢¢ху (xi, уj) = zхуi j.
Требуется построить квадратичную форму Н(x,у) ми-нимально возможной степени, для которой:
Н(xi, уj) = z i j; H¢х (xi, уj) = zхi j, H¢у (xi, уj) = zуi j,
Н¢¢ху (xi, уj) = zхуi j (i = 0,1,..., n; j = 0,1,..., m),
т.е. в узлах сетки помимо значений заданной функции двух переменных z (x, у) совпадают величины её частных и смешанной производных по x, у.
В скалярном виде искомую квадратичную форму можно представить как:
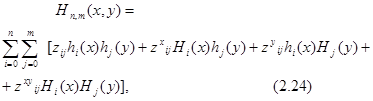
где hi (x), hj (y), Нi (x), Нi (y), Нj (x), Нj (y) – те же cпециальные функции, что и у полиномов Эрмита для двукратных узлов.
В векторном виде данная форма Эрмита может быть представлена следующим образом:
Нn,m (x,у) =`H(x)Т Z`H(y); (2.25)
где:
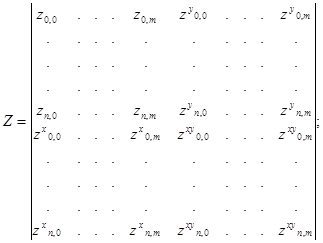
`H(x)= (h0 (x),..., hn (x),Н0 (x),..., Нn (x));
`H(y)= (h0 (y),..., hm (y);Н0 (y),..., Н m (y)).
Рассмотрим интерполирование в безразмерных нор- мированных координатах поверхностей по двукратным узлам на прямоугольном участке сетки [x0,x1]´[у0,y1]. В её граничных точках заданы значения функции z(x, у), её первые и смешанная производные. Переходя к безразмер-ным переменным tх=(x-x0)/hх и tу =(у-y0)/hy ( где hх = x1 - x0, hy = y1 -y0 ), и используя матрицу МЭ, решение для S(tx, ty) можно представить в виде:
S(tx, ty) = (MЭ`Т3х)Т Z (MЭ`Т3y), (2.26)
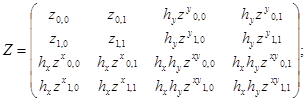
` Тх3 и ` Ту3 - степенные векторы переменных tх и tу.
Задачи.
1. Может ли билинейная поверхность быть представлена в виде квадратичной формы Лагранжа?
2. Можно ли квадратичную форму Лагранжа, построенную по четырем точкам, представить в виде билинейной фор-мы?
3. Доказать, что линии уровня билинейной поверхности по обоим параметрам являются отрезками прямых. Найти их аналитические выражения.
4. Доказать, что линии уровня квадратичной формы Лагранжа, построенной по четырем точкам, являются отрезками прямых. Найти их аналитические выражения.
5. Найти выражения для функций Лагранжа и построить квадратичные формы для следующих случаев интерполи-рования поверхностей по однократным узлам:
|
|
|
а) n=1; х0 = 1; х1 = 2; m =2; y0 = 1; y1 = 2; y2 =3;
z0,0 = 1; z0,1 = 4; z0,2 = 5; z1,0 = 2; z1,1 = 3; z1,2 = 6;
б) n=2;х0 =-2; х1 = -1;х2 = 1; m =2; y0 = 1; y1 = 2; y2 =3;
z0,0 = -10; z0,1 = -6; z0,2 = z1,0 = -4; z1,1 = -2; z1,2 = 0; z2,0 = z2,1 = 1; z2,2 = 4.
6. Найти выражения для функций hi (x), Нi (x), hj(y), Нj (y) и построить квадратичные формы Эрмита для интерполиро-вания поверхностей по двукратным узлам:
а) n=1; х0 = 0; х1 = 2; m =2; y0 = - 1; y1 = 0; y2 =1;
z0,0 = 5; z0,1 = 3; z0,2 = 6; z1,0 = 8; z1,1 = 5; z1,2 = 7;
zх0,0 = 2; zх0,1 = 1; zх0,2 = 0; zх1,0 = 1; zх1,1 = 2; zх1,2 = 0;
zу0,0 = - 1; zу0,1 = 2; zу0,2 = 3; zу1,0 = - 2; zу1,1 = 1; zу1,2 = 3;
б) n=2; х0 = -2; х1 = -1; х2 =1; m =2; y0 = 0; y1 = 1; y2 =2;
z0,0 = -8; z0,1 = -10; z0,2 = z1,0 = -7; z1,1 = -5; z1,2 = -2; z2,0 = -5; z2,1 = -2; z2,2 =1;
zх0,0 = 0; zх0,1 = 1; zх0,2 = 2; zх1,0 = 1; zх1,1 = 2; zх1,2 = zх2,0 = 1; zх2,1 = zх2,2 = 2;
zу0,0 = -1; zу0,1 =1; zу0,2 =3; zу1,0 = 0; zу1,1 =1; zу1,2 =0; zу2,0 = zу2,1 =1; zу2,2 =2.
|
|
|


