 |
Интерполирование по двукратным узлам. Интерполяционные многочлены Эрмита
|
|
|
|
Допустим, в узлах xi (i = 0,1,...,n) заданы не только значения у(xi)=уi, но и первые производные у ¢ (xi)= у ¢ i. Требуется построить полином Н(x) минимально возможной степени, для которого Н(xi) = уi, Н ¢ (xi) = у ¢ i (i = 0,1,...,n).
Данная задача называется интерполированием по дву-кратным узлам, поскольку в каждом из них дано два гео-метрических условия.
Общее число геометрических условий в задаче равно 2n+2. Искомый интерполяционный полином минимально возможного порядка должен иметь степень не выше 2n+1, так как число его неизвестных коэффициентов при кано-ническом задании (2.5) равно 2n+2.
Полином Н(x) имеет вид:
 |
54

 где 1; i = j; 1; i = j;
где 1; i = j; 1; i = j;
hi(xj) = H¢ i (xj) =
0; j ¹ i, 0 £ j £ n; 0; j ¹ i, 0 £ j£ n;
h¢i(xj) = 0; 0 £ j £ n; Hi (xj) = 0; 0 £ j £ n.
Рассмотрим функции Нi (x). В узлах xj (j ¹ i, 0 £ j £ n) у них двойные нули: Hi (xj) = H¢i(xj) = 0. В узле xi -одинарный нуль: Hi (xi) = 0. Полином минимальной степени, удовлетворяющий этим условиям, имеет вид:
Hi (xi) = С [w(х)]2/(x-xi) = C (x -x0)2×(x - x1)2×... × (x –
- xi-1)2× (x-xi) × (x - xi+1)2×... × (x - xn) 2,
где С – некоторая константа.
Величину С находим из условия H¢ i (xj) = 1. Так как H¢i(x) = С[2w(х)w¢(х)/(x-xi) - w(х)2/(x-xi)2], то из H¢ i (xj) = С[w¢(xi)]2 = 1 следует: С = 1/[w¢(xi)]2. Отсюда получаем:
Hi (xi) = [w(х) / w¢(xi)]2/(x-xi) = Фi2(х)(x-xi), (2.14)
где Фi(х) - функция Лагранжа.
Перейдём к построению функций hi (x). В узлах xj (j¹ i, 0 £ j £ n) у них также двойные нули: hi (xj) = h¢i(xj) = 0. В узле xi – следующие условия: hi (xi) = 1; h¢i (xi) =0. Для обеспечения условий в узлах xj в hi (x) вносится множитель вида (w(х))2/(x-xi)2. Для выполнения условий в узле xi в hi (x) дополнительно вводится множитель вида (с + d(x-xi)), у которого с и d – некоторые неизвестные кон-станты. Подставляя формулу в условие hi (xi) = 1, получим: с = 1/(w¢(xi))2. Выражение для hi (x) принимает вид: hi (x) =(w(х))2/(x-xi)2 [1/ (w¢(xi))2 + d(x-xi)].
|
|
|
Производная функции по х:
h¢i (x) = 2 [w(х)/(x-xi)] × [w(х)/(x-xi)]¢x [1/ (w¢(xi))2 + d(x-xi)]+[w(х)/(x-xi)]2×d.
С учётом свойств полинома w(х) условие h¢i (xi) =0 можно представить в виде:
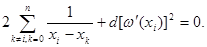 |
Отсюда получим:

В итоге искомая функция может быть представлена в следующей форме:

Подставляя найденные выражения (2.14) и (2.15) в общую формулу (2.13), получим интерполяционную фор-мулу Эрмита для двукратных узлов:
 |
(2.16 а)
В векторном виде интерполяционную формулу Эрмита представляют в виде скалярного произведения:
Н (x) = (`H(x),`Y); (2.16 б)
где `H(x) = (h0 (x),..., hn (x), Н0 (x),..., Н n (x));
`Y = (y0 , y1 ,..., yn , y¢0 , y¢1,..., y¢n ).
Рассмотрим по аналогии с однократными узлами ин-терполирование в двукратных при помощи нормированной переменной. Допустим, в граничных точках отрезка [x0,x1]
заданы по два геометрических условия: у(x0) = у0, у¢(x0) = у¢0, у(x1) = у1, у¢ (x1) = у¢1. Вводя на отрезке [x0,x1] нор-мированную переменную t= (x – x0) / (x1 - x0) и обозначая h = x1 - x0, представим явное решение для S(t) при помощи кубического интерполяционного многочлена Эрмита по формуле (2.16):
S(t)=у0j1(t)+у1j2(t)+h у¢0j3 (t)+h у¢1j4 (t), (2.17а)
где функции j1 (t); j2 (t); j3 (t); j4 (t), называемые полиномами Эрмита, обладают следующими свойствами
j1 (0) = 1; j1 (1) = 0; j¢1 (0) = 0; j¢1 (1) = 0;
j2 (0) = 0; j2 (1) = 1; j¢2 (0) = 0; j¢2 (1) = 0;
j3 (0) = 0; j3 (1) = 0; j¢3 (0) = 1; j¢3 (1) = 0;
j4 (0) = 0; j4 (1) = 0; j¢4 (0) = 0; j¢4 (1) = 1.
Их можно найти подстановкой в формулу Эрмита ли-бо с применением общих методов, изложенных в п.2.2:
j1 (t) = 3(1-t)2 –2(1-t)3 =1-3t2+2t3 = ((1,0,-3, 2),(1,t,t2,t3)) = ((1,0,-3,2),`T 3);
j2 (t) = 3t2 –2t3 = ((0, 0,3,-2),`T 3);
j3 (t) =(1-t)2 – (1-t)3 = t - 2t2+ t3 = ((0, 1, -2,1),`T 3);
j4 (t) = - t 2 + t 3 = ((0, 0,-1,1),`T 3).
С помощью введённых скалярных произведений вектор значений j1(t) - j4(t) представим как произведение:
 |
Используя расширенный вектор значений Y *=(у0, у1, h у¢0, h у¢1), многочлен Эрмита можно представить в виде:
|
|
|
S(t)=( ` Y *, МЭ`Т 3). (2.17 б)
Кубический полином (2.17) обеспечивает в обоих узлах интерполяции не только требуемые значения функции, но и углы наклона касательных.
По аналогии с интерполированием по однократным узлам полином Эрмита может быть выражен через раз-делённые разности. Для этого необходимо наряду с обычными разностями, в которых все аргументы отличны друг от друга, рассмотреть случай с повторяющимися аргу-ментами.
Обозначим верхним индексом повторяемость аргу-мента. Разность порядка 1 с повторяющимся аргументом xi, xi может быть интерпретирована следующим образом:
f(x1i, x2i) =lim f(xi, x¢ i) =f¢(xi ) / (1!).
x¢ i ® x i
В общем случае
f(x1i, x2i,..., xki) =f k-1(xi) / (k-1)!.
В случае двукратных узлов необходимо в разделён-ных разностях повторять дважды каждое значение xi (0 £ i £ n). В результате получим обобщение интерполяционного многочлена Ньютона для двукратных узлов:
HnN(x) = y0 + (x- x0 )f(x0 , x0 ) + (x- x0)2 f(x0 , x0 , x1 ) + (x- x0)2(x- x1) f(x0 , x0 , x1, x1 ) +... +(x- x0)2(x- x1)2 ×... × (x- xn-1)2(x- xn) f(x0 , x0 , x1, x1,..., xn-1 , xn-1 , xn ,xn). (2.18)
С помощью разделённых разностей можно в явном виде построить полином Эрмита для интерполирования по узлам с различающейся степенью кратности. Допустим, требуется интерполировать узлы xi (0 £ i £ n), обладающие, соответственно, кратностями ki (ki ³ 1). Будем обозначать верхним индексом при аргументе номер его вхождения в выражение. В этом случае полином Эрмита будет иметь вид:
HnN(x) = y0 + (x- x0 )f(x10 , x20 ) +... + (x- x0)k0 -1 f(x10 , x20 ,..., x0 k0) + (x- x0)k0 × f(x10 , x20,...,x0k0, x1)+...+ (x- x0)k0(x-
x1)k1×... × (x- xn-1)k(n-1)(x- xn)kn-1× f(x10 , x20 ,..., x0k0,..., x1n , x2n ,..., xnkn) (2.19)
Пример. На множестве двукратных узлов x0 = - 2; x1 = 1; x2=3 заданы значений функции у(x) и её первой произ-водной у ¢ (x):
у(x0)=у0 =6; у(x1)=у1=2; у(x2) = у2 =3; у¢(x0)=у¢0 =-2; у¢(x1)=у¢1 =-1; у¢(x2)= у¢2 = 1.
Построить на этом множестве узлов:
1) полином Эрмита Н(x) минимально возможной степени,
2) обобщённый многочлен Ньютона.
Решение.
1. Вспомогательный полином w(х) и функции Лагранжа будут следующими:
w(х)= (x+2)(x-1)(x-3);

По формулам (2.14),(2.15) строим функции Нi (x) и hi (x).
H0 (x) =(х-1)2(х-3)2(x+2) / 152;
H1 (x) = (х+2)2(х-3)2(x-1) / 62;
 |
H2 (x) =(х+2)2(х-1)2(x-3) / (10)2;
По формуле (2.16) многочлен Эрмита принимает вид:
 |
Упрощая, получим:
 |
2. Рассчитаем разделённые разности:
1-й порядок:
|
|
|
f(x10, x20) = у¢0 = - 2;
f(x20, x11) = (у1 - у0)/(x1 - x0 )=(2-6) / (1-(-2)) = - 4/3;
f(x11, x21) = у¢1 = -1;
f(x21, x12) = (у2 - у1)/(x2 - x1)=1 / 2;
f(x12, x22) = у¢2 = 1.
2-й порядок:
f(x10, x20, x11) = (-4 / 3 – (-2)) / 3 = 2 / 9;
f(x20, x11, x21) = (-1 – (-4/3)) / 3 = 1 / 9;
f(x11, x21, x12) = (1/2 – (-1)) / 2 = 3/4;
f(x21, x12, x22) = (1 – 1 / 2) / 2 = 1 / 4.
3-й порядок:
f(x10, x20, x11, x21) = (1 / 9 – 2 / 9) / 3 = - 1 / 27;
f(x20, x11, x21, x12) = (3 / 4 – 1 / 9) / 5 = 23 / 180;
f(x11, x21, x12, x22) = (1 / 4 – 3 / 4) / 2 = - 1 / 4.
4-й порядок:
f(x10, x20, x11, x21, x12) = (23 / 180 – (-1 /27)) / 5 = 89 / 540;
f(x20, x11, x21, x12, x22) = (- 1 / 4 – 23 / 180) / 5 = - 17 / 45.
5-й порядок:
f(x10,x20,x11,x21,x12,x22) = (-17/45 – 89/540)/5 = 293 / 2700.
Обобщённый многочлен Ньютона по формуле (2.19):
HnN(x) = 6 - 2(x + 2) + 2(х+ 2)2 / 9 - (x+ 2)2(x- 1) / 27 +
+ 89(x+2)2(x- 1)2 / 540 +293(x+2)2(x- 1)2 (x-3)/ 2700.
Задачи.
1. Найти выражения для функций hi (x) и Нi (x) и построить полиномы Эрмита для следующих случаев интерполи-рования по двукратным узлам:
а) задача 1 из п.2.1,
б) задача 1 г) из п.2.2,
в) n=2; х0 = -2; х1 = 0; х2 =2;
у(х0)=-8; у¢(х0)=2; у(х1)=1; у¢(х1)=0; у(х2) = -1; у¢ (х2) = - 2;
г) n=3; х0 = 0; х1 = 1; х2 =2; х3 =4;
у(х0) = 10; у¢ (х0) = - 1; у(х1) = 6; у¢ (х1) =0; у(х2) = 1;
у¢ (х2) = 2; у(х3) = 4; у¢ (х3) = 1.
2. Найти разделённые разности и построить обобщенные интерполяционные многочлена Ньютона для геометри-ческих условий из задач 1 а), 1 б), 1в), г).
|
|
|


