 |
Конические поверхности и поверхности вращения.
|
|
|
|
Определение. Поверхностью вращения называется поверхность, образованная вращением какой-либо плоской линии вокруг прямой, лежащей в плоскости этой линии.
Для вывода уравнения поверхности вращения необходимо выбрать систему координат. Чтобы уравнение поверхности вращения выглядело проще, ось вращения принимают за одну из координатных осей.
Пусть в координатной плоскости Oyz задана кривая L уравнением F(Y, Z)=0 (рис. 24). Вращаем кривую L вокруг оси Oy. Получим некоторую поверхность. Пусть M(x, y, z) - произвольная точка получившейся поверхности. Тогда 
, но 
т.к. если взять точку M1 с отрицательной аппликатой, то
Следовательно, имеем Y = y, 
и координаты точки M(x, y, z) удовлетворяют уравнению
Уравнение (62) и есть искомое уравнение поверхности вращения.
Т. о., чтобы получить уравнение поверхности, образованной вращением линии L, лежащей в плоскости Oyz, вокруг оси Oy, нужно в уравнении этой линии заменить z на 
Аналогичные правила будут иметь место и по отношению к уравнениям поверхностей, полученных вращением плоских линий вокруг других координатных осей.
Сфера и эллипсоид.
Определение: Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид
| ( |
где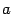 
, 
, 
-- положительные числа.
Исследуем форму эллипсоида. Из уравнения (13.3) видно, что координаты точек поверхности ограничены: 
, 
, 
.
Эллипсоид обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат. Доказывается это так же, как в предложении 12.1.
Для выяснения формы эллипсоида рассмотрим его сечения плоскостями. Найдем линию пересечения эллипсоида с плоскостью 
. Так как любая точка плоскости имеет нулевую третью координату, 
, то координаты точек эллипсоида на плоскости удовлетворяют уравнению
|
|
|
| (13.4) |
По теореме 12.2 получаем, что линия пересечения является эллипсом с полуосям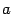и и (рис. 13.3).
Рис.13.3.Сечение плоскостью
Аналогично, сечение в плоскости 
дает эллипс
с полуосями и , а сечение плоскостью 
-- эллипс
с полуосям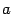и и (рис. 13.4)
Рис.13.4.Сечения эллипсоида координатными плоскостями
Нарисованный "каркас" из сечений уже дает представление об эллипсоиде. Но чтобы выяснить, как ведет себя поверхность между нарисованными кривыми, рассмотрим сечение эллипсоида плоскостью 
. Эта плоскость параллельна плоскости и пересекает ось 
в точке 
. Уравнения этой линии
Очевидно, что если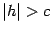 
, то ни одна точка пространства не может удовлетворять этой системе: в левой части первого уравнения стоит неотрицательное число, а в правой -- отрицательное.
Если 
, то сечении получим лишь одну точку 
или 
в зависимости от знака .
Пусть 
. Тогда первое уравнение преобразуем к виду
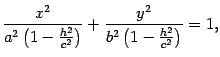
то есть к виду
| (13.5) |
где 
, 
. Уравнение (13.5) является уравнением эллипса, подобного эллипсу, задаваемому уравнением (13.4), с коэффициентом подобия 
и полуосями 
и 
. Ясно, что сечение плоскостью 
является таким же эллипсом, расположенным симметрично первому относительно плоскости . Нарисуем эти сечения (рис. 13.5).
Рис.13.5.Дополнительные сечения эллипсоида
Таким образом, весь эллипсоид составлен из эллипсов, лежащих в плоскостях, параллельных плоскости и подобных эллипсу в плоскости . Рисунок 13.6 дает более привычное глазу изображение эллипсоида.
Рис.13.6.Эллипсоид
Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии -- центром эллипсоида. Числа 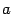, , называются полуосями. Если полуоси попарно различны, то эллипсоид называется трехосным.
|
|
|
Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей. Например, если 
, то все сечения эллипсоида плоскостями , , будут окружностями. Сам эллипсоид может быть получен из эллипса
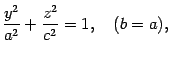
лежащего в плоскости , при вращении его вокруг оси (рис. 13.7).
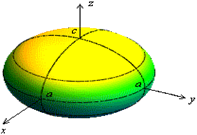
Рис.13.7.Эллипсоид вращения
|
|
|
