 |
Эллиптический и гиперболический параболоиды.
|
|
|
|
Определение 13.7 Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
| (13.13) |
где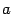 
и 
-- положительные числа.
Исследуем форму эллиптического параболоида. Он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости 
, 
и координатная ось 
.
Для построения эллиптического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 
. На этой плоскости 
, поэтому
Координаты только одной точки плоскости могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью . На этой плоскости 
, поэтому
Это уравнение параболы на плоскости . Построим ее (рис. 13.19). Сечение плоскостью также является параболой. Нарисуем и ее (рис. 13.19). Найдем линии пересечения поверхности с плоскостью 
. Уравнения этой линии
Очевидно, что только одна точка (начало координат) удовлетворяет этим уравнениям, если 
. Эта точка называется вершиной параболоида.
Пусть 
. Первое уравнение преобразуем к виду
то есть к виду
| (13.14) |
где 
, 
. Уравнение (13.14) является уравнением эллипса. Нарисуем полученное сечение (рис. 13.19). При 
плоскость поверхность не пересекает.
Рис.13.19.Сечения эллиптического параболоида координатными плоскостями
Найдем сечения параболоида плоскостями 
, параллельными плоскости . Линии этих сечений удовлетворяют уравнениям
и являются параболами, такими же, как в плоскости , только сдвинутыми вверх на величину 
, их вершины при таком сдвиге лежат на параболе, получившейся в сечении плоскостью (рис. 13.20).
Рис.13.20.Дополнительные сечения параболоида
|
|
|
Следовательно, вся поверхность может быть получена движением параболы, лежащей в плоскости . Парабола должна двигаться так, чтобы ее плоскость была параллельна плоскости , а вершина скользила по параболе в плоскости .
Привычное для глаза изображение приведено на рисунке 13.21.
Рис.13.21.Эллиптический параболоид
Если в уравнении (13.13) 
, то сечения плоскостями, параллельными плоскости , являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости , вокруг оси (рис. 13.22).
Рис.13.22.Параболоид вращения
Определение 13.8 Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
| (13.15) |
где 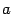и -- положительные числа.
Исследуем форму гиперболического параболоида. Так же, как и эллиптический параболоид, он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости , и координатная ось .
Для построения гиперболического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому
Это уравнение определяет на плоскости пару прямых 
, изображенных на рисунке 13.23.
Найдем линию пересечения с плоскостью . На этой плоскости , поэтому
Это уравнение на плоскости задает параболу, ветви которой направлены вниз. Построим ее (рис. 13.23). Сечение плоскостью также является параболой
но ее ветви направлены вверх. Нарисуем и ее (рис. 13.23).
Рис.13.23.Сечения гиперболического параболоида координатными плоскостями
Найдем линии пересечения поверхности с плоскостью 
, . Уравнения этой линии
Первое уравнение преобразуем к виду
то есть к виду
| (13.16) |
где , . Уравнение (13.16) является уравнением гиперболы. Ее действительная ось параллельна оси 
, а мнимая -- оси 
. Полуоси равны соответственно 
и 
. Нарисуем полученное сечение, но чтобы не перегружать рисунок линиями, асимптоты изображать не будем (рис. 13.24).
|
|
|
Найдем линии пересечения с плоскостями 
, параллельными плоскости . Уравнения этих линий
Первое из этих уравнений является уравнением параболы, такой же, как и в сечении плоскостью , только сдвинутой вдоль оси на величину 
вверх. Эти параболы изображены на рисунке 13.24.
Рис.13.24.Изображение гиперболического параболоида с помощью сечений
Так как 
-- произвольное число, то вся поверхность может быть получена движением параболы, лежащей в плоскости . Передвигать параболу нужно так, чтобы ее плоскость оставалась параллельной плоскости , а вершина скользила по параболе в плоскости .
Плоскость , , пересекает поверхность по гиперболе, но в отличие от гиперболы (13.16), ее действительная ось параллельна теперь оси , а мнимая -- оси (рис. 13.25).
Рис.13.25.Дополнительное сечение
Привычное для глаза изображение приведено на рисунке 13.26.
Рис.13.26.Гиперболический параболоид
|
|
|
