 |
Отображения множеств. Функция. Биекция.
|
|
|
|
Для решения вопроса о том, равное ли число элементов содержат два множества A и B, можно поступить двумя способами. Первый способ состоит в подсчёте числа элементов в каждом множестве и сравнении полученных натуральных чисел. Второй способ не требует знания количества элементов в каждом из множеств А и В. Он состоит в попытке установить между множествами А и B взаимно однозначное соответствие (биекцию). Если биекцию f:А→ B удалось отыскать, то это означает, что количество элементов в А и B одинаково. Например, если в трамвае каждый пассажир сидит на сидении, и при этом нет ни свободных мест, ни стоящих пассажиров, то тем самым установлено взаимно однозначное соответствие (биекция) между множеством пассажиров и множеством посадочных мест, поэтому число сидений в данном трамвае равно числу севших в него пассажиров. Хотя второй метод несёт меньше информации, чем первый (он устанавливает равенство числа элементов в множествах А и B, но не указывает самого числа), у него есть преимущество применимости для количественного сравнения бесконечных множеств.
Определение: Множество A называется эквивалентным множеству B, если существует биекция f:А→B. В этом случае говорят также, что множество A имеет одинаковую мощность с множеством B. Обозначение: A ~ B или 
.
Примеры
1. Множество всех натуральных чисел 
эквивалентно множеству 
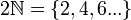всех чётных чисел, так как отображение 
, определяемое формулой f(n)=2n есть биекция.
2. Функция 
взаимно однозначно отображает интервал 
на все множество действительных чисел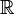 
. Поэтому 
. (Заметим: оказывается, в ограниченном интервале содержится столько же точек, сколько и на всей бесконечной числовой прямой!)
|
|
|
3. Функция f=(b-a)x+a взаимно однозначно отображает интервал (0,1) на интервал (a,b), а сегмент [0,1] на сегмент [ a,b ], поэтому (0,1)~(a,b); [0,1]~[a,b].
Теорема 1:
1. Всегда A~A;
2. Если A~B, то B~A.
3. Если A~B и B~C, то A~C.
Доказательство строится на определении эквивалентного множества и свойств биекции:
1. Тождественное отображение id: A→A есть биекция.
2. Если f:А→B - биекция, то и обратное отображение f-1:B→A — биекция.
3. Если f:A→B и g:B→C - биекции, то и их композиция f•g:A→C - биекция.
Теорема 2: Если A1~B1, A2~B2,то 
.
Доказательство
Пусть f1:A1→B1 и f2:A2→B2 - биекции. Определим отображение 
формулой f(a1,a2)=(f1(a1), f2(a2)). Тогда f есть биекция, так как для любого элемента (b1, b2) декартова произведения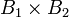 
в декартовом произведении 
имеется единственный прообраз относительно отображения f, именно точка 
.
Tеорема 3: Пусть 
и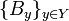 
- два семейcтва попарно непересекающихся множеств, и пусть существует такая биекция: f:X→Y, что A x~ B f(x) для любого элемента 
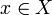. Тогда множества 
и 
эквивалентны.
Доказательство
Обозначим через g x биекцию множества А x на множество B f(x). Пусть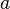 
- произвольный элемент из А. Тогда, так как множества первого семейства попарно не пересекаются, существует единственный элемент 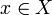, такой, что 
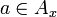. Поставим в соответствие элементу a элемент gx(a) из Bf(x), принадлежащий вместе с тем и множеству B. Получим биекцию множества А на B. Действительно, если b произвольный элемент из B, то в силу попарной непересекаемости множеств второго семейства, существует единственный элемент 
, такой, что 
. Ясно, что элемент 
является единственным прообразом элемента b при нашем соответствии.
Tеорема 4: Если 
и A3~A1, то A2~A1.
Доказательство
Так как A1~A3, то существует биекция f: A1→A3. Положим 
и далее по индукции, если множества A1, A2,...An уже определены, то полагаем 
. Таким образом, получается последовательность множеств 
. Покажем, что эта последовательность удовлетворяет следующим трем условиям:
|
|
|
1. 
(1)
2. для всех m≠n 
(2)
3. для всех 
(3)
Докажем условие (1) по индукции. Отношения 
выполнены по условию теоремы. Допустим, что верны отношения 
. Тогда из 
следует 
, то есть 
. Тем самым условие (1) доказано.
Условие (2) вытекает из (1), так как при m≠n полагая, например, m>n, будем иметь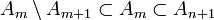 
. Следовательно, любая точка из Am\Am+1 не принадлежит An\An+1.
Для доказательства (3) заметим, что из отношений 
и биективности f следует 
, что и означает справедливость отношений (3).
Положим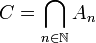 
. Тогда справедливы равенства (4): 
и (5): 
, причём слагаемые в них попарно не пересекаются.
Докажем, например, равенство (4). Из соотношений (1) следует, что все слагаемые правой части равенства (4) содержатся в его левой части. Докажем обратное включение. Пусть 
. Если 
, то 
принадлежит и всей правой части. Если же 
, то существует такоЙ номер n, что 
. Пусть m - наименьший из номеров, для которого 
. Так как , то m ≥ 2. Ясно, что 
. Поэтому 
. Следовательно, принадлежит и всей правой части равенства (4), что и завершает его доказательство.
Докажем еще, что слагаемые в правой части равенства (4) попарно не пересекаются. Первое слагаемое С не пересекается с любым слагаемым 
в силу очевидного включения 
, а остальные слагаемые попарно не пересекаются в силу (2).
Если положить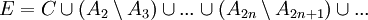 
, то равенства (4) и (5) можно переписать следующим образом: 
. В этих двух объединениях слагаемые, стоящие на одинаковых местах, начиная со второго, эквивалентны в силу (3), а первые слагаемые одинаковы и потому тоже эквивалентны. По теореме 3: множества A1 и A2 эквивалентны.
Понятие эквивалентности двух множеств было бы бессодержательным, если б оказалось, что все бесконечные множества эквивалентны между собой. Однако это не так, что и вытекает из следyщей теоремы.
Теорема 5 (Теорема Кантора):. Множество X и его булеан (множество всех его подмножеств) 
не эквивалентны.
Доказательство
Допустим противное, что 
. Тогда существует биекция: 
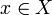. Для любого элемента f(x) есть элемент булеана , то есть подмножество множества X. Возможны две ситуации: либо 
, либо 
. Обозначим через Y множество всех таких элементов 
, что 
. Множество Y одновременнно является элементом булеана . Поэтому существует такой единственный элемент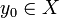 
, что f(y0)= Y. Ясно, что либо 
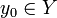, либо 
. Покажем, что оба эти отношения невозможны, что и докажет теорему.
|
|
|
Пусть 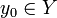. Но Y = f(y0), значит 
. Но в таком случае по определению Y . Получили противоречие.
Пусть теперь 
. Но такой элемент должен по определению множества Y принадлежать Y: 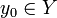. Опять получилось противоречие.
|
|
|
