 |
Пример 2: сопоставление двух эмпирических распределений
|
|
|
|
Интересно сопоставить данные, полученные в предыдущем примере, с данными обследования X. Кларом 800 испытуемых (Klar H ., 1974, р. 67). X. Кларом было показано, что желтый цвет является единственным цветом, распределение которого по 8 позициям не отличается от равномерного. Для сопоставлений им использовался метод % Полученные им эмпирические частоты представлены в Табл. 4.18.
Таблица 4.18
Эмпирические частоты попадания желтого цвета на каждую из 8 позиций в исследовании X. Клара (по: Klar H., 1974) (n =800)

Сформулируем гипотезы.
Н0: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара не различаются.
H1: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара отличаются друг от друга.
Поскольку в данном случае мы будем сопоставлять накопленные эмпирические частости по каждому разряду, теоретические частости нас не интересуют.
Все расчеты будем проводить в таблице по алгоритму 15.
АЛГОРИТМ 15
Расчет критерия λ при сопоставлении двух эмпирических распределений
1. Занести в таблицу наименования разрядов и соответствующие им эмпирические
частоты, полученные в распределении 1 (первый столбец) и в распределении 2
(второй столбец).
2. Подсчитать эмпирические частости по каждому разряду для распределения 1
по формуле:
f *э= f э/ n 1
где f э - эмпирическая частота в данном разряде;
п 1 - количество наблюдений в выборке. Занести эмпирические частости распределения 1 в третий столбец.
3. Подсчитать эмпирические частости по каждому разряду для распределения 2
по формуле:
f *э= f э/ n 2
где f э - эмпирическая частота в данном разряде;
n2 - количество наблюдений во 2-й выборке.
|
|
|
Занести эмпирические частости распределения 2 в четвертый столбец таблицы.
4. Подсчитать накопленные эмпирические частости для распределения 1 по формуле:

где Σ f *j-1 - частость, накопленная на предыдущих разрядах;
j - порядковый номер разряда;
f* j-1 - частость данного разряда.
Полученные результаты записать в пятый столбец.
5. Подсчитать накопленные эмпирические частости для распределения 2 по той
же формуле и записать результат в шестой столбец.
6. Подсчитать разности между накопленными частостями по каждому разряду.
Записать в седьмой столбец абсолютные величины разностей, без их знака.
Обозначить их как d.
7. Определить по седьмому столбцу наибольшую абсолютную величину разности
8. Подсчитать значение критерия λ по формуле:
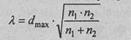
где п 1 - количество наблюдений в первой выборке;
n 2 - количество наблюдений во второй выборке.
9. По Табл. XI Приложения 1 определить, какому уровню статистической зна-
чимости соответствует полученное значение λ.
Если λэмп > 1,36, различия между распределениями достоверны.
Последовательность выборок может быть выбрана произвольно, так как расхождения между ними оцениваются по абсолютной величине разностей. В нашем случае первой будем считать отечественную выборку, второй - выборку Клара.
Таблица 4.19
Расчет критерия при сопоставлении эмпирических распределений желтого цвета в отечественной выборке (n 1=102) и выборке Клара (n 2=800)

Максимальная разность между накопленными эмпирическими частостями составляет 0,118 и падает на второй разряд.
В соответствии с пунктом 8 алгоритма 15 подсчитаем значение Я,:
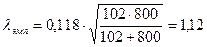
По Табл. XI Приложения 1 определяем уровень статистической значимости полученного значения: р=0,16
Построим для наглядности ось значимости.

На оси указаны критические значения λ, соответствующие принятым уровням значимости: λ 0,05=1 ,36, λ0,01=1,63.
|
|
|
Зона значимости простирается вправо, от 1,63 и далее, а зона незначимости - влево, от 1,36 к меньшим значениям.
λэмп>λкр
Ответ: Н0 принимается. Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара совпадают. Таким образом, распределения желтого цвета в двух выбор-ках не различаются, но в то же время они по-разному соотносятся с равномерным распределением: у Клара отличий от равномерного распределения не обнаружено, а в отечественной выборке различия обнаружены (ρ<0,05). Возможно, картину могло бы прояснить применение другого метода?
Е.В. Гублер (1978) предложил сочетать использование критерия λ, с критерием φ* (угловое преобразование Фишера).
Об этих возможностях сочетания методов λ и φ* мы поговорим в следующей главе (см. пример 4 п.5.2).

|
|
|


