Пример с укрупнением разрядов признака

Тест Мюнстерберга для измерения избирательности перцептив­ного внимания в адаптированном варианте М.Д. Дворяшиной (1976) предъявлялся студентам факультета психологии Ленинградского универ­ситета (n₁=156) и артистам балета Мариинского театра (n ₂=85). Мате­риал методики состоит из бланка с набором букв русского алфавита, в случайном порядке перемежающихся. Среди этого фона скрыто 24 сло­ва разной степени сложности: "факт", "хоккей", "любовь", "конкурс", "психиатрия" и т.п. Задача испытуемого возможно быстрее отыскать их и подчеркнуть (Дворяшина М.Д., 1976, с. 124). Совпадают ли рас­пределения количества ошибок (пропусков слов) в двух выборках (Табл. 4.13)?

Таблица 4.13

Эмпирические частоты пропуска слов в тесте Мюнстерберга в двух выборках испытуемых (по данным М.Д. Дворяшиной, Е.В. Сидоренко, 1973)

разряды	Эмпирические частоты пропуска слов
В группе студентов (n1=156)	В группе артистов балета (n2=85)	Суммы
I. 0 пропусков II. 1 пропуск III. 2 пропуска IV. 3 пропуска V. 4 пропуска VI. 5 пропусков VII. 6 пропусков VIII. 7 пропусков IX. 8 пропусков X. 9 пропусков
Суммы

Сформулируем гипотезы.

Н₀: Распределения ошибок (пропусков слов) в выборках студентов и артистов балета не различаются между собой.

H₁: Распределения ошибок (пропусков слов) в выборках студентов и артистов балета различаются между собой.

Прежде чем перейти к расчету теоретических частот, обратим внимание на последние 4 значения признака, от 6 пропусков и ниже. Очевидно, что f _теор для любой из ячеек последних 4 строк таблицы бу­дет меньше 5. Например, для ячейки, отмеченной кружком:

f _теор=5*85/241=1,763

Полученная теоретическая частота меньше 5.

Для того, чтобы решить, какие разряды нам следует укрупнить, чтобы f _теор была не меньше 5, выведем формулу расчета минимальной суммы частот по строке по формуле:

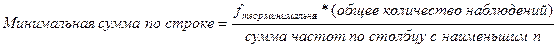
В данном случае столбцом с наименьшим количеством наблюде­ний является столбец, относящийся к выборке артистов балета (n =85). Определим минимальную сумму частот для каждой строки: Минимальная сумма по строке =5*241/85=14,16 Мы видим, что для получения такой суммы нам недостаточно объединения последних 4 строк Табл. 4.13, так как сумма частот по ним меньше 14 (5+3+2+1=11), а нам необходима сумма частот, пре­вышающая 14. Следовательно, придется объединять в один разряд пять нижних строк Табл. 4.13: теперь любое количество пропусков от 5 до 9 будет составлять один разряд.

Однако это еще не все. Мы видим, далее, что в строке "4 про­пуска" сумма составляет всего 8. Значит, ее необходимо объединить со следующей строкой. Теперь и 3, и 4 пропуска будут входить в один разряд. Все остальные суммы по строкам больше 14, поэтому мы не нуждаемся в дальнейшем укрупнении разрядов.

Эмпирические частоты по укрупненным разрядам представлены в Табл. 4.14.

Таблица 4.14

Эмпирические частоты пропуска слов по укрупненным разрядам в двух выборках испытуемых

Разряды	Эмпирические частоты пропуска слов
В группе студентов (n1=156)	В группе артистов балета (n2=85)	Суммы
I. 0 пропусков II. 1 пропуск III. 2 пропуска IV. 3-4 пропуска V. 5-9 пропусков		А В Д Ж И		Б Г Е З К
Суммы

Исследователю бывает огорчительно терять информацию, заведо­мо утрачиваемую при укрупнении разрядов. Например, в данном случае нас может интересовать, удалось ли сохранить специфический для вто­рой выборки спад частот на 3 и 4 пропусках и резкий их подъем на 5 пропусках (Рис. 4.7).

Сравним графики на Рис. 4.7 и Рис. 4.8. Мы видим, что спад частот во второй выборке на 3-х и 4-х пропусках сохранился, а спад на 2-х пропусках в первой выборке стал еще более заметным. В то же время все возможные различия в частотах в диапазоне от 5-и до 9-и пропусков теперь оцениваются только глобально, по соотношению об­щих сумм частот в этих диапазонах. По графику на Рис. 4.8 мы уже не можем определить, какое максимальное количество пропусков встре­чается в первой группе и какое - во второй. Сопоставление распределе­ний на этом конце становится более грубым.

Если бы у нас было больше испытуемых в выборке артистов ба­лета, то, возможно, удалось бы сохранить подъем частоты на 5-и про­пусках. Сейчас же нам придется довольствоваться сопоставлением по данным укрупненным разрядам.

Перейдем к подсчету теоретических частот для каждой ячейки Табл. 4.14

f _{А теор}=115*156/241=74,44

f _{Б теор}=115*85/241=40,56

f _{В теор}=47*156/241=30,41

f _{Г теор}=47*85/241=16,59

f _{Д теор}=27*156/241=17,47

f _{Е теор}=27*85/241=9,53 f _{Ж теор}=27*156/241=17,47

f _{З теор}=27*85/241=9,53 f _{И теор}=25*156/241=16,18 f _{К теор}=25*85/241=8,82

Определим количество степеней свободы V по формуле: ν=(k -l)*(c- l) где k - количество строк (разрядов),

с - количество столбцов (выборок). Для данного случая: ν=(5-l)*(2-l)=4

Все дальнейшие расчеты произведем в таблице по Алгоритму 13. Поправка на непрерывность не требуется, так как v>l.

Таблица 4.15

Расчет критерия χ2 при сопоставлении двух эмпирических распределений пропусков слов в тесте Мюнстерберга (n ₁=156, n ₂=85)

Ячейки таблицы частот	Эмпирическая частота взгляда (fэj)	Теоретическая частота (fт)	(fэj-fт)	(fэj-fт)2	(fэj-fт)2/ fт
А Б В Г Д Е Ж З И К		74,44 46,56 30,41 16,59 17,47 9,53 17,47 9,53 16,18 8,82	18,56 -18,56 -3,41 3,41 -6,47 6,47 2,53 -2,53 -11,18 11,18	344,47 344,47 11,63 11,63 41,86 41,86 6,401 6,401 124,99 124,99	4,63 8,49 0,38 0,70 2,40 4,40 0,37 0,67 7,72 14,17
Суммы			0,00		43,95

По Табл. IX Приложения 1 определяем критические значения при ν =4:

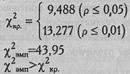
Ответ: Н₀ отвергается. Принимается Н₁. Распределения про-пусков слов в выборках студентов и артистов балета различаются меж­ду собой (р<0,01).

В распределении ошибок у артистов балета можно заметить два выраженных максимума (0 пропусков и 5 пропусков), что может ука­зывать на два возможных источника ошибок[9].

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: