 |
Проверка гипотез о законе распределения
|
|
|
|
Выше рассматривались гипотезы, относящиеся к отдельным параметрам распределения случайных величин, причем модели законов распределения этих величин предполагались известными. Однако во многих практических задачах модель закона распределения заранее не известна и возникает задача выбора модели, согласующейся с результатами наблюдений случайной величины.
Пусть высказано предположение, что неизвестная функция распределения Fэмп(x) исследуемой случайной величины Х имеет вполне определенную модель Fтеор(x), т.е. высказана гипотеза: H0: Fэмп(x) = Fтеор(x). В качестве теоретической модели может быть рассмотрена нормальная, показательная, равномерная или какая-либо другая модель. Это определяется сущностью изучаемого явления, а также результатами предварительной обработки полученных экспериментальных данных (видом гистограммы, полигона частот, соотношением основных числовых характеристик).
Критерии, с помощью которых проверяется гипотеза о законе распределения, называются критериями согласия. Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, т. е. согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, называют теоретическим. Обычно эмпирические и теоретические частоты различаются в силу того, что:
· расхождение случайно и связано с ограниченным количеством наблюдений;
· расхождение неслучайно и объясняется тем, что статистическая гипотеза о теоретическом законе распределения – ошибочна.
|
|
|
Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой гипотезы о модели распределения экспериментальных данных.
Таблица 3. Определение теоретических частот основных распределений
| Распределение | Параметры распределения | Теоретические частоты | Критерий |
| Нормальное | 

|  , ,
 , ,  – Приложение 1 – Приложение 1
|  Критическая область – правосторонняя
Критическая область – правосторонняя
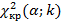 , k = m - r - 1 , k = m - r - 1
|
| Показательное |  = = 
| 
| |
| Равномерное | 

| 
|
Критерий согласия Пирсона. Критерий основан на сравнении эмпирических и теоретических частот. Эмпирические частоты получают в результате эксперимента, а теоретические частоты рассчитывают по формулам (табл. 3). Предварительно необходимо найти точечные оценки параметров предполагаемого распределения по выборке, а затем использовать их для вычисления теоретических частот.
Критерий имеет  - распределение с k = m - r - 1 степенями свободы, где m – число интервалов вариационного ряда; r - число параметров теоретического распределения, вычисленных по экспериментальным данным. Однако критерий имеет
- распределение с k = m - r - 1 степенями свободы, где m – число интервалов вариационного ряда; r - число параметров теоретического распределения, вычисленных по экспериментальным данным. Однако критерий имеет  - распределение лишь при n
- распределение лишь при n  , поэтому необходимо, чтобы в каждом интервале было достаточное количество данных. Малочисленные эмпирические частоты (ni эмп < 5) следует объединить с соседним интервалом, в этом случае и соответствующие им теоретические частоты также складываются. Если производилось объединение частот, то при определении числа степеней свободы следует в качестве m принять число интервалов, оставшихся после объединения частот.
, поэтому необходимо, чтобы в каждом интервале было достаточное количество данных. Малочисленные эмпирические частоты (ni эмп < 5) следует объединить с соседним интервалом, в этом случае и соответствующие им теоретические частоты также складываются. Если производилось объединение частот, то при определении числа степеней свободы следует в качестве m принять число интервалов, оставшихся после объединения частот.
Пример 9. В таблице представлены изменения выработки на одного основного рабочего. Проверить гипотезу, что выработка рабочих цеха распределена по нормальному закону.
| Выработка, % | 94-100 | 100-106 | 106-112 | 112-118 | 118-124 | 124-130 | 130-136 | 136-142 |
| Число рабочих |
Первоначально определяем характеристики:  ;
;  . В предположении, что выработка рабочих цеха распределена нормально, вычисляем теоретические частоты:
. В предположении, что выработка рабочих цеха распределена нормально, вычисляем теоретические частоты:
|
|
|
 ;
;  ;
;  = 1,5 и т.д. В результате имеем:
= 1,5 и т.д. В результате имеем:
 , чел. , чел.
| 1,5 | 5,9 | 14,1 | 22,8 | 24,7 | 18,2 | 8,7 | 2,9 |
После объединения малочисленных частот число интервалов сокращается:

| 
| ||||||

| 7,4 | 14,1 | 22,8 | 24,7 | 18,2 | 11,6 |
1. Принимаем 
2. Назначаем  .
.
3. Критерий:  , k = m – 2 – 1 = 6 – 3 = 3.
, k = m – 2 – 1 = 6 – 3 = 3.
4.  .
.
5. Согласно критерию критическая область W – правосторонняя:  .
.
6. Т.к.  нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.
нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.
7. Вывод: предположение о том, что выработка рабочих цеха распределена нормально, согласуется с данными исследования.
Критерий Колмогорова. Критерий Колмогорова в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривает максимальное значение абсолютной величины разности между эмпирической и теоретической функцией распределения. Первоначально по выборочным данным определяют точечные оценки параметров предполагаемого распределения. Затем строится эмпирическая функция распределения по данным выборки. Теоретическая функция распределения строится по предполагаемому закону распределения. Наблюдаемое значение критерия сравнивают с критическим значением (табл. 4) и делают соответствующий вывод.
Таблица 4. Критерий Колмогорова
| Распределение | Параметры распределения | Теоретические частоты | Критерий | ||||||||||
| Нормальное | 

|  Приложение 2
Приложение 2
| 

| ||||||||||
| Критическая область – правосторонняя | |||||||||||||
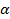
| 0,40 | 0,30 | 0,20 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 | |||

| 0,89 | 0,97 | 1,07 | 1,22 | 1,36 | 1,48 | 1,63 | 1,73 | 1,95 | 2,03 | |||
Пример 10. По данным примера 9 проверить гипотезу, что выработка рабочих цеха распределена по нормальному закону с помощью критерия Колмогорова.
Первоначально определяем характеристики:  ;
;  . Функции распределения (эмпирическую и теоретическую) удобнее строить с помощью таблицы:
. Функции распределения (эмпирическую и теоретическую) удобнее строить с помощью таблицы:

| |||||||||

| 0,010 | 0,030 | 0,100 | 0,210 | 0,410 | 0,690 | 0,880 | 0,980 | 1,000 |

| 0,004 | 0,021 | 0,080 | 0,221 | 0,449 | 0,695 | 0,878 | 0,964 | 0,993 |
1. Принимаем 
2. Назначаем  .
.
3. Критерий: 
4.  .
.
5. Согласно критерию критическая область W – правосторонняя:  .
.
6. Т.к.  нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.
нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.
|
|
|
7. Вывод: предположение о том, что выработка рабочих цеха распределена нормально, согласуется с данными исследования.
Проверка гипотез об однородности выборок
Гипотезы об однородности выборок – это гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности. Пусть имеются две независимые выборки, полученные из генеральных совокупностей с неизвестными теоретическими функциями распределения F1(x) и F2(x). Проверяемая нулевая гипотеза имеет вид H0: Fэмп 1(x) = Fэмп 2(x) против конкурирующей гипотезы H1: Fэмп 1(x)  Fэмп 2(x).
Fэмп 2(x).
Критерий Колмогорова-Смирнова использует ту же самую идею, что и критерий Колмогорова, но только в критерии Колмогорова сравнивают эмпирическую и теоретическую функцию распределения, а в этом критерии сравнивают две эмпирические функции распределения. Критерий Колмогорова-Смирнова имеет вид:  , где
, где  . При достаточно больших объемах выборок (n > 50) для определения критических значений используют таблицы критерия Колмогорова (табл. 4). Для малых выборок (n < 20) необходимо использовать специальные таблицы.
. При достаточно больших объемах выборок (n > 50) для определения критических значений используют таблицы критерия Колмогорова (табл. 4). Для малых выборок (n < 20) необходимо использовать специальные таблицы.
Критерий Вилкоксона относится к ранговым критериям однородности выборок. Ранговый критерий основан не на значениях случайной величины, полученных в выборке, а на порядковых номерах (рангах) этих значений, которые проранжированы.
Предварительно выборки нумеруют: традиционно первой выборкой считается та, объем которой меньше. После этого варианты обеих выборок располагают в возрастающем порядке в виде одного вариационного ряда и присваивают им ранги (порядковые номера). Далее в этом ряду находят сумму рангов вариант первой выборки – это и есть наблюдаемое значение критерия Вилкоксона wнабл. Сравнивая наблюдаемое значение критерия и критические точки делают вывод об однородности выборок. При вычислении наблюдаемого значения критерия необходимо учитывать, что варианты разных выборок могут совпадать. В таких случаях говорят о наличии "связанных рангов", а соответствующим совпадающим величинам приписывают среднее арифметическое тех рангов которые они занимают.
|
|
|
Таблица 4. Критические точки критерия Вилкоксона
| Объем выборок | Критические точки | |
n1  n2 n2  25 25
| нижняя | wнижн. кр(  /2, n1, n2), Приложение 9 /2, n1, n2), Приложение 9
|
25 < n1  n2
или n1 < 25 < n2 n2
или n1 < 25 < n2
| нижняя | wнижн. кр  ,
Ф(zкр) = (1 – α) /2, Приложение 2 ,
Ф(zкр) = (1 – α) /2, Приложение 2
|
| - | верхняя | wверхн. кр = (n1 + n2 + 1)n1 - wнижн. кр |
Пример 10. Предложены два метода увеличения выхода продукции А и В. При уровне значимости 0,05 проверить гипотезу об их одинаковой эффективности:
| А (№1) | 17 | 22 | 3 | 5 | 15 | 7 | 13 | 66 | 15 | - |
| В (№2) | 47 | 30 | 2 | 28 | 1 | 21 | 7 | 44 | 29 | 33 |
Построим общий вариационный ряд и присвоим ранги:
| Ранги | 3 | 4 | 5,5 | 5,5 | 7 | 8 | 9 | 10 | ||
| Варианты | 1 | 2 | 3 | 5 | 7 | 7 | 13 | 15 | 15 | 17 |
| № выборки | 2 | 2 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 |
| Ранги | 12 | 19 | - | |||||||
| Варианты | 21 | 22 | 28 | 29 | 30 | 33 | 44 | 47 | 66 | - |
| № выборки | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | - |
1. Принимаем H0: Fэмп 1(x) = Fэмп 2(x)
2. Назначаем  .
.
3. Критерий: w = Σ рангов первой выборки.
4. wнабл = 3+4+5,5+7+8+9+10+12+19 = 77,5
5. Согласно H1: Fэмп 1(x)  Fэмп 2(x) критическая область W – двусторонняя: wнижн. кр(
Fэмп 2(x) критическая область W – двусторонняя: wнижн. кр(  /2, n1, n2) = w(0,025;9;10) = 65 и wверхн. кр = (9 + 10 +1)9 – 65 = 115.
/2, n1, n2) = w(0,025;9;10) = 65 и wверхн. кр = (9 + 10 +1)9 – 65 = 115.
6. Т.к. wнижн. кр = 65 < wнабл = 77, 5 < wверхн. кр = 115 нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.
7. Вывод: предположение о том, что два метода увеличения выхода продукции одинаково эффективны согласуется с данными исследования.
|
|
|


