Представление результатов измерений с учетом их погрешностей

 

Как было отмечено ранее, под погрешностью измерения будем понимать совокупность всех ошибок измерения.

Ошибки измерений

 

Ошибки измерений классифицируют по следующим видам:

Абсолютные и относительные.

Положительные и отрицательные.

Постоянные и пропорциональные.

Грубые, случайные и систематические.

Прочие.

Абсолютная ошибка единичного результата измерения (А­ _y) определяется как разность следующих величин:

А­ _y = y _i - y _ист.» y _i -` y.

 

Относительная ошибка единичного результата измерения (В­ _y) рассчитывается как отношение следующих величин:

.

 

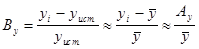Из этой формулы следует, что величина относительной ошибки зависит не только от величины абсолютной ошибки, но и от значения измеряемой величины. При неизменности измеряемой величины (y) относительную ошибку измерения можно уменьшить только за счет снижения величины абсолютной ошибки (А­ _y). При постоянстве абсолютной ошибки измерения для уменьшения относительной ошибки измерения можно использовать прием увеличения значения измеряемой величины.

Пример. Допустим, что в магазине торговые весы имеют постоянную абсолютную ошибку измерения массы: A_m = 10 г. Если Вы взвесите на таких весах 100 г конфет (m₁), то относительная ошибка измерения массы конфет составит:

.

При взвешивании на этих же весах 500 г конфет (m₂) относительная ошибка будет в пять раз меньше:

.

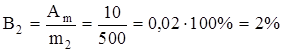Таким образом, если Вы будете пять раз взвешивать по 100 г конфет, то вы из-за ошибки измерения массы, из 500 г недополучите суммарно 50 г продукта. При однократном взвешивании большей массы (500 г) Вы потеряете только 10 г конфет, т.е. в пять раз меньше.

Учитывая вышесказанное, можно отметить, что в первую очередь необходимо стремиться к уменьшению относительных ошибок измерения. Абсолютные и относительные ошибки можно рассчитать только после определения среднего арифметического значения результата измерения.

Знак ошибки (положительный или отрицательный) определяется разницей между единичным и фактическим результатом измерения:

y _i -` y > 0 (ошибка положительная);

y _i -` y < 0 (ошибка отрицательная).

Если абсолютная ошибка измерения не зависит от значения измеряемой величины, то такая ошибка называется постоянной. В противном случае ошибка будет пропорциональной. Характер ошибки измерения (постоянная или пропорциональная) определяется после проведения специальных исследований.

Грубая ошибка измерения (промах) - это значительно отличающийся от других результат измерения, который обычно возникает при нарушении методики измерения. Наличие грубых ошибок измерения в выборке устанавливается только методами математической статистики (при n>2). С методами обнаружения грубых ошибок познакомьтесь самостоятельно в [1,6,8,9].

Деление ошибок на случайные и систематические достаточно условно.

К случайным ошибкам относят ошибки, которые не имеют постоянной величины и знака. Такие ошибки возникают под действием следующих факторов: неизвестных исследователю; известных, но нерегулируемых; постоянно изменяющихся.

Случайные ошибки можно оценить только после проведения измерений.

Количественной оценкой модуля величины случайной ошибки измерения могут являться следующие параметры: 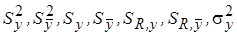и др.

Случайные ошибки измерения невозможно исключить, их можно только уменьшить. Один из основных способов уменьшения величины случайной ошибки измерения - это увеличение числа единичных измерений (увеличение величины n). Объясняется это тем, что величина случайных ошибок обратно пропорциональна величине n, например:

.

 

Систематические ошибки - это ошибки с неизменными величиной и знаком или изменяющиеся по известному закону. Эти ошибки вызываются постоянными факторами. Систематические ошибки можно количественно оценивать, уменьшать и даже исключать.

Систематические ошибки классифицируют на ошибки I, II и III типов.

К систематическим ошибкам I типа относят ошибки известного происхождения, которые могут быть до проведения измерения оценены путем расчета. Эти ошибки можно исключить, вводя их в результат измерения в виде поправок. Примером ошибки такого типа является ошибка при титрометрическом определении объемной концентрации раствора, если титрант был приготовлен при одной температуре, а измерение концентрации проводилось при другой. Зная зависимость плотности титранта от температуры, можно до проведения измерения рассчитать изменение объемной концентрации титранта, связанное с изменением его температуры, и эту разницу учесть в виде поправки в результате измерения.

Систематические ошибки II типа - это ошибки известного происхождения, которые можно оценить только в ходе эксперимента или в результате проведения специальных исследований. К этому типу ошибок относят инструментальные (приборные), реактивные, эталонные и др. ошибки. Познакомьтесь с особенностями таких ошибок самостоятельно в [9].

Любой прибор при его применении в процедуре измерения вносит в результат измерения свои приборные ошибки. При этом часть этих ошибок случайная, а другая часть - систематическая. Случайные ошибки приборов отдельно не оценивают, их оценивают в общей совокупности со всеми другими случайными ошибками измерения.

Каждый экземпляр любого прибора имеет свою персональную систематическую ошибку. Для того чтобы оценить эту ошибку, необходимо проводить специальные исследования.

Наиболее надежный способ оценки приборной систематической ошибки II типа - это сверка работы приборов по эталонам. Для мерной посуды (пипеток, бюреток, цилиндров и др.) проводят специальную процедуру - калибровку.

На практике наиболее часто требуется не оценить, а уменьшить или исключить систематическую ошибку II типа. Самыми распространенными методами уменьшения систематических ошибок являются методы релятивизации и рандомизации. Познакомьтесь с этими методами самостоятельно в [9].

К ошибкам III типа относят ошибки неизвестного происхождения. Эти ошибки можно обнаружить только после устранения всех систематических ошибок I и II типов.

К прочим ошибкам отнесем все другие виды ошибок, не рассмотренные выше (допустимые, возможные предельные ошибки и др.). Понятие возможных предельных ошибок применяется в случаях использования средств измерения и предполагает максимально возможную по величине инструментальную ошибку измерения (реальное же значение ошибки может быть меньше величины возможной предельной ошибки).

При использовании средств измерения можно рассчитать возможные предельные абсолютную (П` y,пр.) или относительную (Е` y,пр.) погрешности измерения. Так, например, возможная предельная абсолютная погрешность измерения находится как сумма возможных предельных случайных (x<sub>` y , случ., пр.</sub>) и неисключенных систематических (d` y, пр.) ошибок:

П` y,пр.= x<sub>` y , случ., пр.</sub> + d` y, пр.

 

При выборках малого объема (n £ 20) неизвестной генеральной совокупности, подчиняющейся нормальному закону распределения, случайные возможные предельные ошибки измерений можно оценить следующим образом:

x<sub>` y , случ., пр.</sub> = D` y = S_{` y} ½t_{P, n}½,
где t_P,n - квантиль распределения (критерий) Стьюдента для вероятности Р и выборки объемом n. Абсолютная возможная предельная погрешность измерения в этом случае будет равна:

П` y,пр.= S<sub>` y</sub> ½t_{P, n}½+ d_{` y ,пр}.

Если результаты измерений не подчиняются нормальному закону распределения, то оценка погрешностей проводится по другим формулам.

Определение величины d_{` y ,пр.</sub> зависит от наличия у средства измерения класса точности. Если средство измерения не имеет класса точности, то за величину d<sub>` y ,пр.} можно принять минимальную цену деления шкалы средства измерения [6, с. 119]. Для средства измерения с известным классом точности за величину d_` y,пр.можно принять абсолютную допустимую систематическую ошибку средства измерения (d _{y , доп.}):

d_` y,пр.» .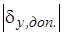

Величина d _{y , доп.} рассчитывается исходя из формул, приведенных в табл.5.

Для многих средств измерения класс точности указывается в виде чисел а×10ⁿ, где а равно 1; 1,5; 2; 2,5; 4; 5; 6 и n равно 1; 0; -1; -2 и т.д., которые показывают величину возможной предельной допускаемой систематической ошибки (Е _{y , доп.}) и специальных знаков, свидетельствующих о ее типе (относительная, приведенная, постоянная, пропорциональная).

Таблица 5

Примеры обозначения классов точности средств измерения

Обозначе­ние класса точности	Формула расчета и значение предельной допускаемой систематической ошибки	Характерис­тика систематической
в доку­мен­тации	на сред­стве из­ме­ре­ния		ошибки
Класс точ­ности 1,5	1,5		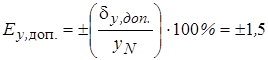Приведенная допускаемая систематичес­кая ошибка в процентах от номинального значения измеряемой величины, которое определяется типом шкалы средства измерения [10]

Продолжение табл.5

Обозначе­ние класса точности	Формула расчета и значение предельной допускаемой систематической ошибки	Характерис­тика систематической
в доку­мен­тации	на сред­стве из­ме­ре­ния		ошибки
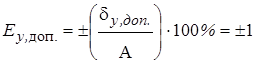
Класс точ­ности 1			Приведенная допускаемая систематичес­кая ошибка в процентах от длины использованной шкалы средства измерения (А) при получении единичных значений измеряемой величины
Класс точ­ности 0,5	0,5		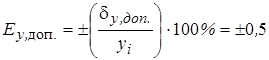Постоянная относительная допускаемая систематичес­кая ошибка в процентах от полученного единичного значения измеряемой величины

 

Окончание табл.5

Обозначе­ние класса точности	Формула расчета и значение предельной допускаемой систематической ошибки	Характерис­тика систематической
в доку­мен­тации	на сред­стве из­ме­ре­ния		ошибки
Класс точ­ности 0,02/ 0,01	0,02/0,01	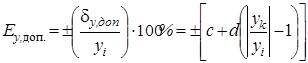c = 0,02 и d = 0,01	Пропорцио­нальная относительная допускаемая систематическая ошибка в долях от полученного единичного значения измеряемой величины, которая возрастает при увеличении конечного значения диапазона измерения данным средством измерения (y k) или уменьшении единичного значения измеряемой величины (y i)

Систематическими ошибками можно пренебрегать, если выполняется неравенство

.

В этом случае принимают, что:

П` y, пр.» x<sub>` y, случ., пр.</sub>» D` y» S<sub>` y</sub> ½t_{P, n}½.

Случайными ошибками можно пренебречь при условии

.

Для этого случая П` y, пр.» d` y,пр..

Увеличение числа единичных измерений является наиболее распространенным методом уменьшения случайных ошибок (что тоже приводит к удорожанию измерений). Увеличивать n целесообразно до тех пор, пока общая погрешность измерения не будет определяться только систематической ошибкой. Минимально необходимое для этого число параллельных измерений (n_min) можно рассчитать только при известном значении генеральной совокупности единичных результатов по формуле

.

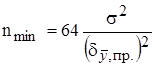Если известны составляющие (m - число составляющих) абсолютной систематической ошибки среднего арифметического результата измерения (), то ее можно оценить по формуле

,

где k - коэффициент, определяемый вероятностью Р и числом m.

Оценка погрешностей измерения зависит не только от средства измерения и объема выборки, но и от типа измерения (прямое это измерение или косвенное).

Деление измерений на прямые и косвенные достаточно условно. В дальнейшем под прямыми измерениями будем понимать такие, когда результат измерения получается непосредственно, например считывается со шкалы прибора. К косвенным измерениям будем относить такие, когда результат измерения рассчитывается как функция (j) результатов одного или нескольких прямых измерений (x ₁, x ₂, …, x _j,.…, x _k).

Необходимо знать, что ошибки косвенных измерений всегда больше, чем ошибки отдельных прямых измерений. Ошибки косвенных измерений оцениваются по соответствующим законам.

 

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: