 |
Линейная математические модель
|
|
|
|
Математические модели
По возможности применения математической модели, основанной на линейных или нелинейных уравнениях, системы автоматического регулирования и управления принято разделять на линейные и нелинейные. Если математическое описание системы сводится к обыкновенным дифференциальным уравнениям, то их называют системами с сосредоточенными параметрами. Системы, математические модели которых содержат уравнения в частных производных, относятся к системам с распределенными параметрами. Линейные и нелинейные системы могут быть описаны дифференциальными, разностными или и теми и другими уравнениями. Соответственно такие системы определяют как непрерывные, дискретные и дискретно-непрерывные. Коэффициенты в уравнениях могут быть постоянными или функциями времени. В первом случае системы называются стационарными, во втором – нестационарными.
Изучение свойств систем автоматического регулирования можно проводить экспериментальными или теоретическими методами. Для экспериментальных исследований создается физическая модель системы автоматического регулирования, отличающаяся от последней размерами. Физическая модель подвергается всесторонним испытаниям для проверки влияния различных факторов на устойчивость, качество и точность регулирования. Перенос результатов исследований, полученных на модели, к натурным условиям осуществляется с использованием законов теории подобия.
Для обобщения экспериментальных результатов и исследования систем автоматического регулирования теоретическими методами, сначала находят математическое описание физических процессов, протекающих в изучаемой системе. Такое описание осуществляется обычно с помощью дифференциальных, интегральных или алгебраических уравнений.
|
|
|
Для расчета любой системы, прежде всего, необходимо составить математическую модель, т. е. получить математическое описание протекающих в системе физических процессов. Если число уравнений равно числу неизвестных переменных, то система уравнений является замкнутой. Замкнутая система уравнений со всеми необходимыми для ее решения начальными и граничными условиями образует математическую модель изучаемой системы.
Исследование свойств изучаемой системы по ее математической модели заключается в решении уравнений численными (приближенными) или аналитическими методами.
Математическое описание системы может быть представлено в форме уравнений “вход-выход” или с использованием переменных состояния.
Линейная математические модель
| В качестве примера проведем математическое описание простой гидромеханической системы, схема которой показана на рис. 4.1. |
|
Уравнение движения массы подвижных элементов системы имеет вид
, (4.1)
где 
и 
– силы, приложенные к массе m соответственно со стороны пружины 1 и гидравлического демпфера 2; 
– суммарная сила трения между поршнем и цилиндром и между штоком и цилиндром; z 2 – перемещение массы m, измеренное от положения равновесия.
Примем за входное воздействие на систему перемещение верхней опоры пружины z 1. Зависимость силы пружины от деформации обычно в практических приложениях считают линейной:
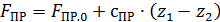, (4.2)
где F ПР.0 – сила, развиваемая пружиной при равновесии массы до приложения к системе воздействия, т. е. при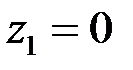 
; c ПР – жесткость пружины. Координату z2 будем отсчитывать от положения массы m при равновесии системы в отсутствии внешнего воздействия на систему. Из уравнений (4.1) и (4.2), для равновесия системы, следует, что
|
|
|
. (4.3)
Сила, развиваемая на демпфере, обусловлена разностью давлений, действующих на поршень со стороны жидкости в верхней и нижней полостях демпфера:
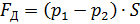, (4.4)
где p 1 и p 2 – давления соответственно в верхней и нижней полостях; S – рабочая площадь поршня.
Расход жидкости через отверстие в поршне демпфера при ламинарном режиме течения пропорционален перепаду давления на дросселе:
, (4.5)
где Q ДР – расход жидкости через дроссель; 
– перепад давления на дросселе; k ДР – проводимость дроссельного отверстия в поршне демпфера.
Для ламинарного режима течения жидкости в цилиндрическом канале диаметром d и длиной l
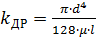(4.6)
(здесь μ – динамический коэффициент вязкости жидкости).
На основании неразрывности потока несжимаемой жидкости можно записать
. (4.7)
Система уравнений (4.1), (4.5) и (4.7) с учетом соотношений (4.2) – (4.4) и (4.6) составляет математическую модель рассматриваемой системы. Полученную систему уравнений можно привести к одному уравнению в форме “вход-выход”, исключив промежуточные переменные и оставив только входную и выходную величины, соответственно z 1 и z 2. При этом все члены с выходной величиной переносят в левую часть уравнения, а все члены с входной величиной – в правую.
Для системы (рис. 4.1) в случае малых сил трения (
) уравнение в форме “вход-выход” будет иметь вид
. (4.8)
Уравнение (4.8) можно записать в общем виде:
, (4.9)
где
; 
; 
; 
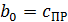; (4.10)
y = z2, u = z 1. (4.11)
Уравнение (4.9) обычно приводят к стандартному виду. Для этого все члены уравнения делим на коэффициент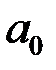 
при выходной величине, в результате получим
. (4.12)
Коэффициенты T 1 и T 2 имеют размерность времени, поэтому называются постоянными времени:
, (4.13)
. (4.14)
Коэффициент K называется коэффициентом передачи или преобразования, или коэффициентом усиления, если он является безразмерной величиной:
. (4.15)
Для системы (рис. 4.1), описываемой уравнением (4.8), можно получить выражения для коэффициентов, используя соотношения (4.10) и (4.13) – (4.15):
, (4.16)
, (4.17)
. (4.18)
Для математического описания системы с использованием переменных состояния дифференциальное уравнение (4.12) второго порядка заменим системой двух уравнений первого порядка:
(4.19)
и соотношением
|
|
|
. (4.20)
Зная пару переменных x 1 и x 2 в некоторый момент времени t 0 и входное воздействие u для всех 
t ³ t 0, можно определить состояние системы в любой момент времени всех t > t 0 и найти значение выходной величины y (t). Величины x 1 и x 2 называются переменными состояния данной системы, а уравнения (4.19) – дифференциальными уравнениями состояния. Соотношение (4.20) устанавливает связь выходной величины с переменной состояния.
|
|
|
