 |
Математические модель электрогидроусилителя
|
|
|
|
Построение математической модели рассмотрим на примере электрогидравлического усилителя, схема которого приведена на рис. 8.4. Электрогидравлический усилитель с золотником, нагруженным пружинами, состоит из электромеханического преобразователя (ЭМП) и гидроусилителя (ГУ), имеющего усилительную ступень в виде сопла-заслонки и управляющую ступень в виде золотникового распределителя. Гидроусилитель состоит из золотника 1, пружин, нерегулируемых дросселей 3, заслонки 4 и сопел.
Электрогидравлический усилитель работает следующим образом. При подаче напряжения на ЭМП в обмотке управления возникает ток, и якорь ЭМП вместе с заслонкой 4 отклоняется от нейтрального положения. Отклонение заслонки 4 от нейтрального положения вызывает изменение расходов через сопла и перепад давлений в полостях А и Б, необходимый для управления золотником 1.
Для обеспечения пропорциональной зависимости перемещений золотника от перемещений заслонки применены пружины 2. Усилие этих пружин при смещении золотника от нейтрального положения уравновешивают силы давлений, приложенные к нему со стороны жидкости в полостях А и Б.
| x З |
| p П |
| p СЛ |
| p 1 |
| p 2 |
| Рис. 8.4. ЭГУ с золотником, нагруженным пружинами |
Описание динамики электрогидроусилителя с золотником, нагруженным пружинами, с учетом массы золотника, силы трения и сжимаемости жидкости выполним при малых отклонениях заслонки от нейтрального положения. За входное воздействие примем отклонение заслонки от нейтрального положения, а за выходную величину, т. е. регулируемую, – перемещение золотника.
Математическое описание начнём с процессов, происходящих в электромеханическом преобразователе. Уравнение вращения якоря запишем в виде
|
|
|
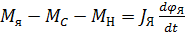 , (8.10)
, (8.10)
где М Я – момент электромагнитных сил, поворачивающих якорь; М С – момент сопротивления, обусловленный силами трения и электромагнитными силами сопротивления, вызванными встречной ЭДС в обмотке управления ЭМП; М Н – момент сил, действующих на заслонку и представляющих нагрузку на якорь; J Я – момент инерции якоря вместе с заслонкой; φЯ – угол отклонения якоря от среднего положения.
Внешнюю моментную характеристику электромеханического преобразователя будем использовать в виде линейной зависимости момента М Я, развиваемого якорем от тока управления i У и угла φЯ поворота якоря:
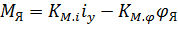 , (8.11)
, (8.11)
где 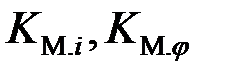 – коэффициенты внешней моментной характеристики ЭМП.
– коэффициенты внешней моментной характеристики ЭМП.
Момент сопротивления М С, возникающий при вращении якоря, будем определять по формуле
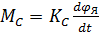 , (8.12)
, (8.12)
где К С – коэффициент сопротивления, обычно определяется экспериментально.
Так как заслонка жестко связана с якорем и имеет возможность поворачиваться вокруг оси совместно с ним, то гидродинамическую силу, приложенную к заслонке, нужно учесть при составлении уравнения вращения якоря.
Момент нагрузки М Н определяется гидродинамической силой F ГД1, обусловленной воздействием на заслонку струй жидкости, истекающих из сопел:
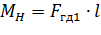 , (8.13)
, (8.13)
где l – расстояние от центра вращения якоря вместе с заслонкой до оси сопел.
Гидродинамическую силу, действующую со стороны потока рабочей жидкости на заслонку, можно определить по формуле
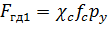 , (8.14)
, (8.14)
где χС – коэффициент, равный 1,03–1,06 для сопел с острыми кромками; 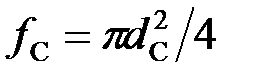 – площадь проходного сечения сопла (здесь d C – диаметр сопла); p y – разность давлений в полостях А и Б (
– площадь проходного сечения сопла (здесь d C – диаметр сопла); p y – разность давлений в полостях А и Б (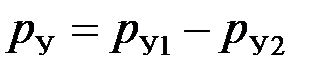 ).
).
После подстановки моментов из формул (8.11)–(8.13) в уравнение (8.10) с учетом соотношения (8.14) получим
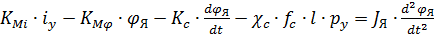 . (8.15)
. (8.15)
Уравнение (8.15) описывает процессы, происходящие в ЭМП. Для электромеханического преобразователя входной величиной является ток i У, подаваемый на обмотки управления, а выходной – угол φЯ поворота якоря. Приведем уравнение к форме “вход-выход”, т. е. в левую часть перенесем члены, содержащие выходную величину φЯ, а в правую – входную i У, в результате получим
|
|
|
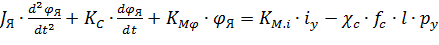 . (8.16)
. (8.16)
В правой части уравнения (8.16) член, содержащий p У, представляет обратную связь, обусловленную действием гидродинамической силы, стремящейся вернуть заслонку с якорем в нейтральное положение.
Разделив все члены уравнения (8.16) на К М.φ, получим его стандартную форму:
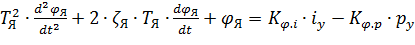 , (8.17)
, (8.17)
где Т Я – постоянная якоря; ζЯ – коэффициент относительного демпфирования якоря; K φ .i – коэффициент преобразования тока i У управления в угол φя поворота якоря; К φ. p – коэффициент преобразования разности давления p y в угол φя поворота. Постоянная времени якоря и коэффициенты преобразования определяются по соотношениям:
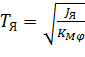 , (8.18)
, (8.18)
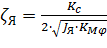 , (8.19)
, (8.19)
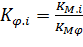 , (8.20)
, (8.20)
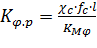 . (8.21)
. (8.21)
Теперь составим математическое описание гидроусилителя. Зависимость расхода жидкости Q у, обеспечивающего перемещение золотника, от отклонения h у заслонки от нейтрального положения и разности давлений p у в полостях А и Б примем линейной:
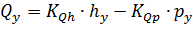 , (8.22)
, (8.22)
где КQ.h и КQ.p – коэффициенты расхода, можно определить экспериментально.
С другой стороны, расход связан с перемещением золотника:
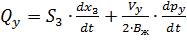 , (8.23)
, (8.23)
где  – площадь торца золотника; d З – диаметр золотника; x З – перемещение золотника; V У – объем каждой из полостей А и Б; B Ж – модуль объемной упругости жидкости. Второе слагаемое в правой части уравнения (8.23) учитывает изменение объема жидкости, обусловленное её сжимаемостью.
– площадь торца золотника; d З – диаметр золотника; x З – перемещение золотника; V У – объем каждой из полостей А и Б; B Ж – модуль объемной упругости жидкости. Второе слагаемое в правой части уравнения (8.23) учитывает изменение объема жидкости, обусловленное её сжимаемостью.
Отклонение заслонки h У от нейтрального положения связано с углом φЯ поворота якоря, при малых отклонениях заслонки можно записать
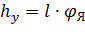 . (8.24)
. (8.24)
Уравнения (8.22)–(8.24) можно заменить одним уравнением в форме “вход-выход”; приняв за входную величину φЯ, а за выходную – p у, получим
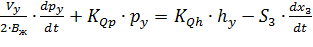 . (8.25)
. (8.25)
Разделив все члены уравнения (8.25) на КQ.p, получим его стандартную форму:
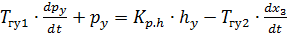 , (8.26)
, (8.26)
где Т ГУ1 и Т ГУ2 – постоянные времени гидроусилителя; К φ. h – коэффициент преобразования перемещения hy заслонки в разность давлений p У. Постоянные времени гидроусилителя и коэффициент преобразования определяются по соотношениям:
|
|
|
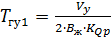 , (8.27)
, (8.27)
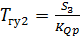 , (8.28)
, (8.28)
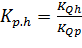 . (8.29)
. (8.29)
Уравнение движения золотника под действием разности давлений в полостях А и Б (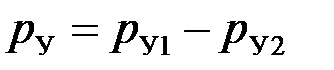 ) можно записать в виде
) можно записать в виде
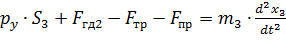 , (8.30)
, (8.30)
где F ГД2 – гидродинамическая сила, действующая на золотник со стороны жидкости, протекающей через распределитель; F ТР – сила трения; F ПР – сила, действующая на торцы золотника со стороны пружин; m З – масса золотника.
Гидродинамическую силу F ГД2 будем считать линейной зависимостью от смещения золотника и определять по формуле
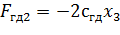 , (8.31)
, (8.31)
где 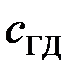 – коэффициент жесткости гидродинамической пружины (гидродинамическая сила имеет линейную зависимость аналогично силе пружины отсюда и название коэффициента).
– коэффициент жесткости гидродинамической пружины (гидродинамическая сила имеет линейную зависимость аналогично силе пружины отсюда и название коэффициента).
Силу трения будем считать вызванной жидкостным трением и определять по формуле
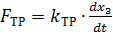 , (8.32)
, (8.32)
где k ТР – коэффициент трения.
Силу от действия пружин на торцы золотника будем определять по формуле
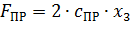 , (8.33)
, (8.33)
где с ПР – жесткость каждой из пружин.
Подставив в уравнение (8.29) выражения для сил, определяемых соотношениями (8.30)–(8.32), и преобразовав его к форме “вход-выход”, получим:
 . (8.34)
. (8.34)
Разделив все члены уравнения (8.34) на коэффициент 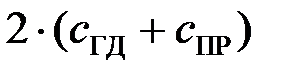 при выходной величине x З, получим:
при выходной величине x З, получим:
 , (8.35)
, (8.35)
где Т ГУ3 – постоянная времени гидроусилителя;ζГУ – коэффициент относительного демпфирования гидроусилителя; К φ. p – коэффициент преобразования разности давления p у в перемещение золотника x З.
Постоянная времени гидроусилителя, коэффициент относительного демпфирования и коэффициент преобразования определяются по соотношениям:
 , (8.36)
, (8.36)
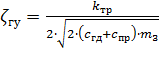 , (8.37)
, (8.37)
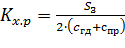 . (8.38)
. (8.38)
Уравнения (8.17), (8.26) и (8.35) с учетом соотношений (8.18)–(8.21), (8.27)–(8.29) и (8.36)–(8.38) составляют математическую модель электрогидравлического усилителя.
При исследовании процессов, протекающих в системах, с помощью ЭВМ и пакетов прикладных программ, основанные на численных методах математическое описание удобнее выполнять в переменных состояния и системы уравнений приводить к дифференциальным уравнениям первого порядка, записанным в форме Коши.
Дифференциальное уравнение (8.17) второго порядка заменим системой двух уравнений первого порядка
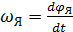 , (8.39)
, (8.39)
|
|
|
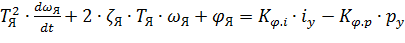 , (8.40)
, (8.40)
где ωя – угловая скорость вращения якоря.
Дифференциальное уравнение (8.35) второго порядка также заменим системой двух уравнений первого порядка
 , (8.41)
, (8.41)
 , (8.42)
, (8.42)
где υ – скорость перемещения золотника.
Уравнение (8.26) с учетом формулы (8.41) можно записать в виде
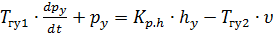 . (8.43)
. (8.43)
Полученную систему уравнение (8.39)-(8.43) приведем к форме Коши:
 .
.
|
|
|


