 |
Нелинейная математическая модель
|
|
|
|
В качестве примера приведем описание простой гидравлической системы, схема которой показана на рис. 5.2. Система состоит из распределителя 1 с постоянным гидравлическим сопротивлением, регулируемого дросселя 2 с золотником 6, гидроцилиндра 3 с поршнем 4 и штоком 5, массы m. Сопротивлением гидролиний будем пренебрегать. В этом случае давление после распределителя 1, перед регулируемым дросселем и в гидроцилиндре будет одинаковым (p 2). На поршень с одной стороны действует сила давления жидкости, а с другой – сила тяжести mg. Поршень находится в равновесии, когда эти силы равны. Изменяя гидравлическое сопротивление регулируемого дросселя перемещением золотника, можно изменять давление p 2 и скорость подъема массы m. Это приводит к нарушению равновесия сил, действующих на поршень, и к его перемещению.
| Рис. 5.2. Гидравлическая система |
| p 3 |
| m |
| p 1 |
| p 2 |
| y |
| Q 2 |
Масса m с помощью штока жестко связана с поршнем, поэтому при перемещении поршня будет перемещаться и масса m.
Гидравлическое сопротивление регулируемого дросселя можно изменять за счет изменения его проходного сечения. Таким образом, изменяя проходное сечение регулируемого дросселя 2, перемещением x золотника, можно управлять положением y массы m (рис. 5.2).
Будем считать давление p 1 перед распределителем и давление p 3 после дросселя постоянными, причем p 1 > p 3.
При показанных на схеме направлениях течения жидкости с расходами Q 1, Q 2 и Q 3 можно записать:
, (5.9)
, (5.10)
, (5.11)
где μ1 – коэффициент расхода распределителя; f 1 – площадь поперечного сечения канала распределителя; μ2 – коэффициент расхода регулируемого дросселя; d – диаметр золотника регулируемого дросселя; k – коэффициент, зависящий от конструктивного исполнения устройства. Коэффициенты расхода μ1 и μ2 будем считать постоянными.
|
|
|
На основании неразрывности течения, с учетом сжимаемости жидкости в гидроцилиндре можно записать:
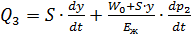, (5.12)
где S – площадь поршня; y – перемещение поршня (массы m); W 0 – объем рабочей полости гидроцилиндра и подводящей гидролинии, соответствующий положению поршня при y = 0; E Ж – модуль объемной упругости жидкости.
На поршень действуют сила давления, сила тяжести и сила вязкого трения. Уравнение движения поршня можно записать в виде
, (5.13)
где F тр – сила вязкого трения между поршнем и цилиндром.
Силу вязкого трения будем определять по соотношению
. (5.14)
С учетом соотношения (5.14) уравнение (5.13) примет вид
. (5.15)
Система уравнений (5.9)–(5.12) и (5.15) представляет собой нелинейную математическую модель рассматриваемой гидравлической системы, потому что содержит нелинейные функции (5.10) и (5.11).
При исследовании процессов, протекающих в системах, с помощью нелинейных математических моделей часто приходится применять ЭВМ и пакеты прикладных программ, основанные на численных методах. В этом случае математическое описание удобнее выполнять в переменных состояния и системы уравнений приводить к дифференциальным уравнениям первого порядка, записанным в форме Коши.
Для примера выполним математическое описание процессов, протекающих в гидравлической системе (рис. 5.2) в переменных состояния.
Введем обозначение
, (5.47)
где υ – скорость поршня и массы m, так как y – перемещение поршня.
С учетом формулы (5.47) система уравнений (5.9)–(5.12) и (5.15) примет вид
. (5.48)
В качестве переменных состояний примем y, p 2 и υ. Подставим в третье уравнение системы (5.48) выражения для расходов Q 1, Q 2 и Q 3 из четвёртого, пятого и шестого уравнений, затем члены, содержащие производные от переменных состояний, перенесём в левые части уравнений, в результате получим систему дифференциальных уравнений первого порядка в форме Коши:
|
|
|
.
(5.49)
При заданных начальных условиях, т. е. при заданных значениях переменных состояний в начальный момент времени t 0:
; (5.50)
; (5.51)
(5.52)
и известном входном воздействии – перемещении золотника x для все t > t 0, т. е.
, (5.53)
можно найти зависимости y (t), υ(t) и p 2(t) для всех t > t0.
Результаты численных расчетов математической модели (5.49) в MathCAD приведены на рис. 5.3–5.5.
| y (t) |
| t |
| Рис. 5.3. Зависимость перемещения поршня от времени |
Из графика (рис. 5.3) можно определить вид переходного процесса (движения поршня), время переходного процесса, количество колебаний, динамическую ошибку и другие параметры переходного процесса.
| υ(t) |
| t |
| Рис. 5.4. Зависимость скорости поршня от времени |
| p 2(t) |
| t |
| Рис. 5.5. Зависимость давления в полости гидроцилиндра от времени |
Зависимости, приведенные на рис. 5.4 и 5.5, позволяют проанализировать характер изменения скорости поршня и колебаний давления в полости гидроцилиндра.
|
|
|
