 |
Математические модель гидроусилителя
|
|
|
|
Составление математической модели рассмотрим на примере гидравлического усилителя, схема которого приведена на рис. 8.4. Гидравлический усилитель с золотником, нагруженным пружинами, состоит из ступени в виде сопла-заслонки и ступени в виде золотникового распределителя. Гидроусилитель включает золотник 1, пружины, нерегулируемые дроссели 3, заслонку 4 и сопела.
Гидравлический усилитель работает следующим образом. Отклонение заслонки 4 от нейтрального положения вызывает изменение расходов через сопла и перепад давлений в полостях А и Б, необходимый для управления золотником 1.
Для обеспечения пропорциональной зависимости перемещений золотника от перемещений заслонки применены пружины 2. Усилие этих пружин при смещении золотника от нейтрального положения уравновешивают силы давлений, приложенные к нему со стороны жидкости в полостях А и Б.
| x |
| P п |
| P сл |
| p 1 |
| p 2 |
| Рис. 8.4. ГУ с золотником, нагруженным пружинами |
Составим математическое описание гидроусилителя. Зависимость расхода жидкости Q у, обеспечивающего перемещение золотника, от отклонения h у заслонки от нейтрального положения и разности давлений p у в полостях А и Б примем линейной:
, (8.1)
где КQ.h и КQ.p – коэффициенты расхода, можно определить экспериментально.
С другой стороны, расход связан с перемещением золотника:
, (8.2)
где 
– площадь торца золотника; d – диаметр золотника; x – перемещение золотника; V у – объем каждой из полостей А и Б; B ж – модуль объемной упругости жидкости. Второе слагаемое в правой части уравнения (8.2) учитывает изменение объема жидкости, обусловленное её сжимаемостью.
Уравнения (8.1)–(8.2) можно заменить одним уравнением в форме “вход-выход”; приняв за входную величину φЯ, а за выходную – p у, получим
|
|
|
(8.3)
Разделив все члены уравнения (8.3) на КQ.p, получим его стандартную форму:
, (8.4)
где Т гу1 и Т гу2 – постоянные времени гидроусилителя; К φ. h – коэффициент преобразования перемещения h y заслонки в разность давлений p у. Постоянные времени гидроусилителя и коэффициент преобразования определяются по соотношениям:
, (8.5)
, (8.6)
. (8.7)
Уравнение движения золотника под действием разности давлений в полостях А и Б (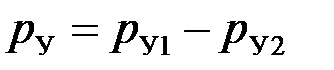
) можно записать в виде
, (8.8)
где F гд2 – гидродинамическая сила, действующая на золотник со стороны жидкости, протекающей через распределитель; F тр – сила трения; F пр – сила, действующая на торцы золотника со стороны пружин; m – масса золотника.
Гидродинамическую силу F гд2 будем считать линейной зависимостью от смещения золотника и определять по формуле
, (8.9)
где 
– коэффициент жесткости гидродинамической пружины (гидродинамическая сила имеет линейную зависимость аналогично силе пружины отсюда и название коэффициента).
Силу трения будем считать вызванной жидкостным трением и определять по формуле
, (8.10)
где k тр – коэффициент трения.
Силу от действия пружин на торцы золотника будем определять по формуле
, (8.11)
где с ПР – жесткость каждой из пружин.
Подставив в уравнение (8.8) выражения для сил, определяемых соотношениями (8.9)–(8.11), и преобразовав его к форме “вход-выход”, получим:
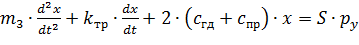. (8.12)
Разделив все члены уравнения (8.12) на коэффициент 
при выходной величине x, получим:
, (8.13)
где Т гу3 – постоянная времени гидроусилителя;ζгу – коэффициент относительного демпфирования гидроусилителя; К φ. p – коэффициент преобразования разности давления p у в перемещение золотника x.
Постоянная времени гидроусилителя, коэффициент относительного демпфирования и коэффициент преобразования определяются по соотношениям:
|
|
|
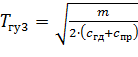; (8.14)
; (8.15)
. (8.16)
Уравнения (8.4) и (8.13) с учетом соотношений (8.5)–(8.7) и (8.14)–(8.16) составляют математическую модель гидравлического усилителя.
При исследовании процессов, протекающих в системах, с помощью ЭВМ и пакетов прикладных программ, основанные на численных методах математическое описание удобнее выполнять в переменных состояния и системы уравнений приводить к дифференциальным уравнениям первого порядка, записанным в форме Коши.
Дифференциальное уравнение (8.13) второго порядка заменим системой двух уравнений первого порядка
, (8.17)
, (8.18)
где υ – скорость перемещения золотника.
Уравнение (8.4) с учетом формулы (8.17) можно записать в виде
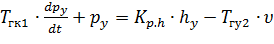. (8.19)
Полученную систему уравнение приведем к форме Коши:
(8.20)
|
|
|
