Распределение трудовых ресурсов

Основной задачей распределения являются расстановка кадров и назначение на должность, обеспечивающие выполнение требуемых видов работ. Задачи распределения являются «зеркальным отображением» задач использования. Если в задачах распределения ресурсов структура работ считается заданной и требуется назначить их исполнителей, то в задачах использования ресурсов заданными являются исполнители, их возможности и индивидуальных характеристики и требуется определить структуру работ которая позволила бы наилучшим образом использовать эти возможности. В большинстве случаев при правлении трудовыми ресурсами решаются одновременно обе задачи.

Задача распределения трудовых ресурсов, для решения которой часто использовались методы исследования операций, решается в организации на двух уровнях управления. На верхнем решается в организации на двух уровнях управления. На верхнем уровне решается задача агрегированного планирования трудовых ресурсов, целью которой является определение численности групп сотрудников, необходимых каждому поздравлению организации; часто эта численность выражается через потребность в человеко-часах и затратах на рабочую силу. Вторым уровнем, на котором решается задача распределения ресурсов, является уровень непосредственного управления. Результатом решения задачи распределения на этом уровне является фактическое назначение каждого конкретного исполнителя на конкретную работу, т.е. решение задачи, которая иногда называется задачей оптимального назначения, дает ответ на вопрос, как назначить n исполнителей (I₁,……I_n) на n работ (J1……Jn), так чтобы максимизировать общую эффективность такого назначения.

Анализ задач распределения трудовых ресурсов осуществляется с помощью моделей транспортного типа, или моделей назначения, программно-целевых моделей, моделей последовательного назначения и имитационных моделей.

 

 

Модели транспортного типа

Основная модель транспортного типа, или модель назначения, имеет следующее математическое выражение:

найти максимум целевой функции

при условиях

, =1

 

где для всех i, j; означает, что I_i назначен на работу J_i, а r_ij есть относительная эффективность каждого исполнителя с точки зрения выполнения им каждого вида работ.

Такое математическое представление модели требует, чтобы каждый исполнитель был назначен на одну и только на одну работу и соответственно на каждую работу должен быть назначен один и только один исполнитель. Сформулированная задача может быть решена с помощью типового алгоритма решения задачи о назначениях или задачи транспортного типа.

Для специалиста, использующего эту модель в реальных ситуациях, наиболее трудным моментом является определение соответствующей целевой функции и, следовательно, соответствующей схемы получения оценок величины r_{i j}. При выборе целевой функции возможно несколько подходов:

1. Максимизация суммы оценок назначений, т.е. требуется найти максимум целевой функции

 

 

В этом случае величина r_{i j} должна непосредственно выражаться через такие важные для организации показатели, как время выполнения работы, издержки производства, объем выпуска в единицу времени и т.д. Однако довольно часто трудно осуществить это, так как каждое значение r_{i j} есть точечная оценка, при получении которой существенную роль играет фактор распределения ошибок. Более того, значение r_{i j} представляет собой прогнозируемую оценку показателей выполнения j-й работы i-м исполнителем. Таким образом, данный подход основан на прогнозировании данных и не лишен недостатков и неопределенностей. Это может привести к тому, что результаты фактической работы организации при использовании назначений, полученных с помощью модели, могут сильно отличаться от тех, которые должны были бы быть при значениях r_{i j} принятых в модели.

2. Максимизация вероятности успешного выполнения каждым исполнителем работы, на которую он назначен, т.е. требуется найти максимум целевой функции

 

P_ij есть вероятность того, что исполнитель I_i успешно выполнит работу J_{j .} Оценки вероятности того, что исполнитель с определенными характеристиками удовлетворительно выполнит каждую из работ, могут быть определены на основе статистических данных. Максимизация вероятности успешного назначения в целом на все работы осуществляется с помощью такого выбора исполнителей для каждой из работ, при котором достигается максимум произведения вероятностей успешного выполнения ими работы. Благодаря свойствам логарифмов целевая функция может быть выражена с помощью приведенной выше формулы. После введения понятия вероятность успеха или неудачи становится возможным рассмотрение других методов оценки значений r_{i j} и подходов к выбору целевой функции. Так, Вейл предложил следующие дополнительные подходы к выбору целевой функции.

1. Максимизация вероятности неуспешного в целом назначения на все виды работ, т.е. требуется найти минимум целевой функции

 

1. Максимизация ожидаемого количества успешных назначений, т.е. требуется найти максимум целевой функции

 

1. Минимизация ожидаемого количества неуспешных назначений, т.е. требуется найти минимум функции

 

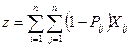
1. Максимизация средних (геометрических) значений вероятностей успеха (P/1 – P) для всех назначений, т.е. требуется найти максимум целевой функции

, 0<P_ij<1

 

 

1. Минимизация средних (геометрических) значений вероятностей [(1-P)/P] для всех назначений, т.е. требуется найти минимум целевой функции

, 0<P_ij<1

 

 

Последние два способа являются общепринятым для решения задач логистики. По мнению Вейла, следует использовать не подход, предусматривающий экстремизация средних значений вероятностей, а подходы 6 и 7, так как они позволяют получить более адекватное распределение вероятностей успеха.

Кроме того, они позволяют осуществить назначения, обеспечивающие максимальное приближение вероятности успеха к единице, в то время как сумма вероятностей дает величину, большую единицы. Однако при этом следует особенно тщательно производить оценку значений r_{i j}, для общих (>0.95) и малых значений (< 0,05) вероятностей. [11]

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: