 |
Законы изменения и сохранения энергии
|
|
|
|
Решение задач
5.1. Частица совершает перемещение по некоторой траектории в плоскости XY из точки 1 с радиус-вектором 
в точку 2 с радиус-вектором 
. При этом на неё действовали некоторые силы, одна из которых 
. Найти работу, которую совершила сила 
. Здесь 
и 
- орты осей X и Y; 
, 
и определены в системе СИ.
Решение. Перемещение происходит под действием постоянной силы, для которой работа определяется как
,
подставив в которое и , получим
.
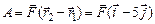Тогда искомая работа силы 
равна
.
5.2. Небольшая муфточка массы m движется по гладкому проводу, изогнутому в горизонтальной плоскости в виде дуги окружности радиуса R (на рис.37 представлен вид сверху). В точке 1, где скорость муфточки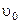 
, на неё начала действовать постоянная горизонтальная сила . Найти скорость муфточки в точке 2.
Решение. Рассмотрим элементарное перемещение муфты 
, тогда элементарная работа силы на этом перемещении равна
,
так как 
(рис.37). Работа силы при перемещении муфточки из точки 1 в точку 2 равна
.
Согласно закону изменения кинетической энергии, приращение кинетической энергии равно работе всех сил, действующих на тело:
.
Из последнего выражения выразим скорость муфточки в точке 2
.
5.3. Брусок массы m находится на горизонтальной плоскости с коэффициентом трения 
. В некоторый момент ему сообщили начальную скорость 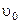. Найти среднюю мощность силы трения за всё время движения бруска 
.
Решение. По определению мощность - это работа, совершаемая силой за единицу времени:
,
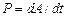средняя мощность
,
где A - работа, совершаемая силой за время .
Работа силы трения, действующей на брусок, определяется изменением его кинетической энергии от 
до 
. Поэтому на основании закона об изменении кинетической энергии
|
|
|
.
Брусок движется по горизонтальной плоскости под действием силы трения, поэтому его скорость в момент времени t определяется выражением
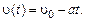
Запишем уравнение движения бруска (второй закон Ньютона) в проекциях на ось X, направленную вдоль его движения
.
Тогда
.
В момент остановки 
скорость бруска равна нулю 
. Поэтому время бруска до остановки равно
.
А искомая средняя мощность равна
.
5.4. В системе отсчёта, вращающейся вокруг неподвижной оси с постоянной угловой скоростью 
, перемещается небольшое тело из точки 1 в точку 2, которые расположены на расстояниях r1 и r2 от оси вращения (r1 > r2). Какую работу совершает при этом центробежная сила инерции?
Решение. Вращающаяся с постоянной угловой скоростью система отсчёта является неинерциальной. Поэтому на тело в такой системе отсчета действует центробежная сила инерции равная 
, где r - и есть расстояние от оси вращения. Работа этой силы по определению равна
.
Из полученного результата видно, что работа центробежной силы не зависит от траектории перемещения. Это значит, что центробежная сила является консервативной силой, а ее поле - потенциально.
5.5. Система состоит из двух последовательно соединённых пружин с жёсткостями k 1 и k 2. Найти минимальную работу, которую необходимо совершить, чтобы растянуть эту систему на 
.
Решение. Работа консервативных сил, действующих на систему, равна убыли потенциальной энергии:
.
Пружину растягивает внешняя неконсервативная сила, величина которой, согласно третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости, которая является консервативной. Поэтому работа внешней силы равна
.
Работа эта будет минимальна, если растяжение совершается достаточно медленно, так чтобы система в любой момент времени находилась в равновесии, то есть
,
где 
и 
- упругие силы, действующие в пружинах 1 и 2 соответственно, 
- внешняя сила (рис.38). В начальном положении пружины не деформированы, поэтому энергия системы равна нулю
|
|
|
.
В конечном положении пружины растянуты, а энергия системы является энергией упругой деформации
,
где 
и 
- растяжение пружин 1 и 2 соответственно.
Воспользовавшись тем, что полное удлинение системы равно 
, а 
то есть 
откуда
и 
,
и 
.
Тогда
,
.
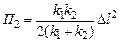5.6*. Потенциальная энергия частицы в некотором поле имеет вид 
, где a и b - положительные постоянные, r - расстояние от центра поля. Найти значение 
, соответствующее равновесному положению частицы. Выяснить, устойчиво ли это положение.
Решение. Частица находится в потенциальном поле. Потенциальная энергия частицы в этом поле - заданная функция одной координаты r. Проекция силы на направление радиус-вектора r может быть определена по формуле
В положении равновесия сила равна нулю:
,
откуда
.
Для построения графика найдем значение r, при которых потенциальная энергия равна нулю
,
.
При 
потенциальная энергия 
. Качественный график зависимости потенциальной энергии от r представлен на рис. 39. Легко видеть, что 
при r, больше r0. Следовательно, положение равновесия характеризуется минимумом потенциальной энергии. И 
соответствует положению устойчивого равновесия.
Законы изменения и сохранения энергии
Механическая энергия системы равна сумме потенциальной и кинетической энергий:
.
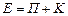Механическая энергия сохраняется, если на систему действуют только консервативные силы. Если система состоит их нескольких тел, то для сохранения механической энергии внутренние силы тоже должны быть консервативными. Применение закона сохранения энергии, связывающего начальное и конечное состояние системы взаимодействующих тел, упрощает решение подобных задач, так как позволяет не рассматривать действующие между телами силы.
Если при переходе системы из начального состояния в конечное на тела системы действовали внешние силы, а в системе действовали диссипативные силы, то
,
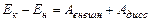где 
и 
- начальная и конечная энергии системы, 
- работа внешних сил, 
- работа диссипативных (неконсервативных) сил.
Кинетическая энергия системы зависит от выбора системы отсчета, изменяясь при переходе от одной системы отсчета к другой. Поэтому, составляя уравнение, выражающее закон сохранения энергии, необходимо рассматривать движение тел в одной и той же инерциальной системе отсчета. В неинерциальной системе отсчета на тела действуют силы инерции, которые всегда являются внешними по отношению к данной системе тел.
|
|
|
При решении задач на основании закона сохранения энергии необходимо:
1) выбрать два положения тела (системы тел);
2) выбрать уровень, от которого отсчитывается потенциальная энергия в поле силы тяжести;
3) вычислить механическую энергию в обоих положениях;
4) если число неизвестных больше числа составленных уравнений, записать уравнение движения тела (второй закон Ньютона).
Решение задач
5.7. Гладкий резиновый шнур, длина которого l и жёсткость k, подвешен одним концом к точке O (см. рис.40). На другом конце имеется упор B. Из точки O начинает падать небольшая муфточка A массы m. Пренебрегая массами шнура и упора, найти максимальное растяжение шнура.
Решение. Рассмотрим два положения муфты: положение I соответствует точке O (рис.40), положение II - моменту, когда шнур максимально растянут. В этом положении скорость муфты равна нулю, максимальное удлинение шнура - .
Потенциальную энергию в поле силы тяжести (П = 0) будем отсчитывать от уровня, при котором шнур максимально растянут.
Вычислим механическую энергию системы в ее начальном I и конечном II положении
, 
.
В обоих положениях кинетическая энергия равна нулю.
На шайбу действуют только консервативные силы mg и сила упругости, следовательно, полная механическая энергия этой системы будет сохраняться
,
.
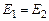После математических преобразований, получим квадратное уравнение относительно
.
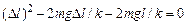Решив которое, найдем:
.
Отрицательный корень уравнения должен быть отброшен, так как он соответствует сжатию шнура, тогда как на самом деле он растягивается. Поэтому
.
5.8. Небольшая шайба массы m начинает скользить, если её положить на вершину шероховатой поверхности полусферы радиусом R. Продолжая скользить, шайба отрывается от полусферы на высоте h от горизонтального основания полусферы. Найти работу сил трения, действующих на шайбу при её соскальзывании.
|
|
|
Решение. Рассмотрим два положения шайбы:
положение I соответствует начальному моменту времени (шайба находится в вершине полусферы),
положение II соответствуетмоменту времени, когда шайба отрывается от полусферы (рис.41). Уровень отсчёта потенциальной энергии в поле силы тяжести обозначен на рисунке П = 0. В положении I шайба покоится и поэтому обладает только потенциальной энергией
.
В момент отрыва шайба движется со скоростью 
, поэтому ее энергия складывается из кинетической и потенциальной
.
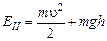В системе действует диссипативная сила трения, поэтому:
.
Подставив в уравнение полученные ранее значения 
и 
, получим
. (1)
Уравнение содержит две неизвестных и 
. Поэтому запишем уравнение движения шайбы (второй закон Ньютона). В момент отрыва N = 0. Выберем ось X в направлении нормального ускорения, и в проекциях на эту ось
,
где 
(рис.41). Тогда, скорость шайбы в момент отрыва равна 
. Подставив полученную скорость в уравнение в (1), получим
,
.
|
|
|
