 |
Совместное применение законов сохранения
|
|
|
|
Если рассматриваемая система состоит из двух взаимодействующих между собой тел, то совместно используются законы сохранения импульса и энергии системы.
Сюда относятся задачи на упругий удар или взаимодействие тел, представляющих собой замкнутую систему, когда отсутствуют диссипативные силы (трения, упругих деформаций) и когда у тел в результате взаимодействия изменяются скорости. При этом сохраняется как импульс, так и энергия системы.
В случае неупругого удара полная механическая энергия системы не сохраняется, она частично или полностью переходит во внутреннюю энергию (тела нагреваются). В этом случае изменение механической энергии равно работе диссипативных сил 
. Импульс системы при этом сохраняется.
Иногда решение задачи упрощается, если ее решать в системе центра масс (раздел IV). В этой и только в этой системе отсчета суммарная кинетическая энергия частиц может обращаться в нуль в случае их относительного покоя. Энергия системы частиц в такой системе складывается из суммарной энергии 
частиц в системе центра масс и энергии, связанной с движением системы частиц как целого (движение центра масс)
.
Решение задач
5.9*. На гладкой горизонтальной плоскости находятся две небольшие шайбы с массами m 1 и m 2, соединённые между собой невесомой пружиной. Шайбам сообщили начальные скорости 
и 
, направления которых взаимно перпендикулярны и лежат в горизонтальной плоскости. Найти механическую энергию этой системы в системе её центра масс.
Решение. Кинетическая энергия системы частиц (рис.42) складывается из суммарной кинетической энергии 
в системе центра масс и кинетической энергии, связанной с движением системы частиц как целого
|
|
|
,
где - кинетическая энергия в системе центра масс, 
– скорость центра масс (раздел IV), равная
.
Таким образом
.
По условию 
, поэтому 
, поэтому
.
Поскольку в системе действуют только консервативные силы, потенциальная энергия системы не меняется, следовательно 
:
.
5.10. Частица A массы m, пролетая вблизи другой, первоначально покоившейся частицы B, отклоняется на угол 
. Импульс частицы A до взаимодействия был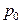 
, после взаимодействия стал p. Найти массу частицы B, если система замкнутая.
Решение. По условию рассматриваемая система замкнута, поэтому согласно закону сохранения импульса, импульс системы сохраняется
,
где M и 
- масса и скорость частицы B. Преобразуем векторное уравнение в скалярное (рис.43)
(1)
Используя связь между величиной импульса и кинетической энергии 
, запишем закон сохранения энергии:
. (2)
Выразим из (2) 
и, подставив эту величину в (1), получим массу частицы B
.
5.11. Небольшая шайба массы m без начальной скорости соскальзывает с гладкой горки высотой h и попадает на доску массы M, лежащую у основания горки на гладкой горизонтальной плоскости. Вследствие трения между шайбой и доской шайба тормозится и, начиная с некоторого момента, движется вместе с доской как единое целое. Найти суммарную работу сил трения в этом процессе.
Решение. Весь путь шайбы можно разбить на два этапа: первый этап – движение по гладкой горке (участок 1-2 на рис.44), второй этап - движение по шероховатой доске (участок 2-3 на рис.). Уровень отсчёта потенциальной энергии обозначен на рисунке П = 0.
Рассмотрим движение шайбы по горке (участок 1-2). В начальный момент времени (точка 1) шайба обладает только потенциальной энергией 
. В момент попадания на доску (точка 2, уровень П = 0) шайба обладает только кинетической энергией 
, где 
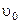- скорость шайбы в точке 2. Горка гладкая, поэтому энергия шайбы сохраняется
,
,
|
|
|
откуда скорость шайбы в момент ее попадания на доску (точка 2) равна
.
Рассмотрим движение шайбы по шероховатой доске (участок 2-3). Силы, действующие между шайбой и доской внутренние, все внешние силы компенсируют друг друга, поэтому 
, где 
- импульс шайбы в момент ее попадания на доску, 
- импульс системы шайба-доска, когда скорости шайбы и доски сравнялись (шайба относительно доски покоится)
,
где 
- скорость системы шайба-доска, которая равна
.
Согласно закону изменения механической энергии системы
.
Учитывая, что 
, последнее уравнение примет вид
,
подставив в которое значение , полученное ранее, найдем работу сил трения
.
5.12. В результате упругого столкновения частицы массы m 1 с покоившейся частицей массы m 2, она отскочила под прямым углом к своему первоначальному направлению движения. Какую относительную часть кинетической энергии потеряла налетающая частица?
Решение. В задаче рассматриваются две упруго взаимодействующие частицы, следовательно, применимы законы сохранения импульса и энергии.
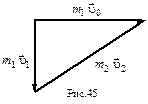Согласно закону сохранения импульса
,
где 
- скорость налетающей частицы до столкновения, - её скорость после столкновения, - скорость первоначально покоившейся частицы после столкновения. На рис.45 закон сохранения импульса представлен в виде сложения векторов, из которого скалярное выражение закона
. (1)
До соударения кинетическая энергия налетающей частицы 
. Поскольку удар упругий, то энергия, потерянная налетающей частицей, равна энергии, полученной первоначально покоившейся частицей, следовательно
,
где 
- относительную часть кинетической энергии, которую потеряла налетающая частица. Разделим уравнение (1) на 
:
. (2)
Согласно закону сохранения энергии:
.
Разделим полученное уравнение на :
. (3)
Решив систему уравнений (1), (2) и (3) относительно , получим
,
,
.
5.13*. Гладкий лёгкий горизонтальный стержень AB может вращаться без трения вокруг вертикальной оси, проходящей через его конец A. На стержне находится небольшая муфточка массы m, соединённая невесомой пружиной длины l 0 с концом A. Жёсткость пружины равна k. Какую работу надо совершить, чтобы эту систему медленно раскрутить до угловой скорости 
?
Решение. Выберем систему отсчета, связанную с Землей. Рассмотрим два состояния системы (рис.46). В состоянии I стержень и муфта покоятся, и пружина не деформирована. В этом состоянии механическая энергия системы
|
|
|
.
В состоянии II стержень и муфта вращаются с угловой скоростью , и пружина деформирована (растянута) на величину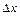 
. Так как стержень вращается плавно, в этом состоянии механическая энергия системы складывается из кинетической энергии муфты и потенциальной энергии упругой деформации пружины
.
Работа внешней силы равна изменению механической энергии системы
.
Величину растяжения пружины определим из уравнения движения (второго закона Ньютона), записанного в проекции на ось X (рис.46). В состоянии II муфта находится в равновесии, поэтому
,
,
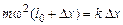откуда 
.
После подстановки 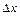найдем искомую работу внешней силы
.
VI. Момент импульса.
|
|
|
